11种排序算法（Python实现）

10种排序算法（Python实现）

冒泡排序

1、 两重循环，每次都将一个点移动到最终位置

def BubbleSort(lst):
    n=len(lst)
    if n<=1:
        return lst
    for i in range (0,n):
        for j in range(0,n-i-1): # 每轮确定一个点的最终位置
            if lst[j]>lst[j+1]:
                (lst[j],lst[j+1])=(lst[j+1],lst[j])
    return lst
x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in  y:
    arr.append(int(i))
arr=BubbleSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
    print(i,end=' ')

快速排序

快排具体算法执行流程如下：https://www.cnblogs.com/MOBIN/p/4681369.html

1、每次都会确定基准值的最终位置

2、快排使用到了，分页和递归

def QuickSort(lst):
    # 此函数完成分区操作，并且返回该元素的最终位置
    def partition(arr, left, right):
        # 执行快排的过程
        key = left  # 使用第一个数为基准数
        while left < right:
            # 如果列表后边的数,比基准数大或相等,则前移一位直到有比基准数小的数出现
            while left < right and arr[right] >= arr[key]:
                right -= 1
            # 如果列表前边的数,比基准数小或相等,则后移一位直到有比基准数大的数出现
            while left < right and arr[left] <= arr[key]:
                left += 1
            # 此时已找到一个比基准大的书，和一个比基准小的数，将他们互换位置
            (arr[left], arr[right]) = (arr[right], arr[left])

        # 当从两边分别逼近，直到两个位置相等时结束，将左边小的同基准进行交换
        (arr[left], arr[key]) = (arr[key], arr[left])
        # 返回目前基准所在位置的索引
        return left

    def quicksort(arr, left, right):
        if left >= right:
            return

        # 获取一个元素的最终位置
        mid = partition(arr, left, right)
        # 递归调用
        # print(arr)
        quicksort(arr, left, mid - 1)
        quicksort(arr, mid + 1, right)

    # 主函数
    n = len(lst)
    if n <= 1:
        return lst
    quicksort(lst, 0, n - 1)
    return lst

print("<<< Quick Sort >>>")
x = input("请输入待排序数列：\n")
y = x.split()
arr = []
for i in y:
    arr.append(int(i))
arr = QuickSort(arr)
# print(arr)
print("数列按序排列如下：")
for i in arr:
    print(i, end=' ')

插入排序（有序+无序）

插入排序算法流程：1 从第二个元素开始，第一个默认为有序，将取出的元素放到前面有序的队列中，放的时候是平移。n2时间复杂度。注意这里比较的时候顺便挪动，因此是两重循环

def InsertSort(lst):
    n=len(lst)
    if n<=1:
        return lst
    for i in range(1,n):
        j=i
        target=lst[i]            #每次循环的一个待插入的数
        while j>0 and target<lst[j-1]:       #比较、后移，给target腾位置
            lst[j]=lst[j-1]
            j=j-1
        lst[j]=target            #把target插到空位
    return lst

x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in  y:
    arr.append(int(i))
arr=InsertSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
    print(i,end=' ')

希尔排序

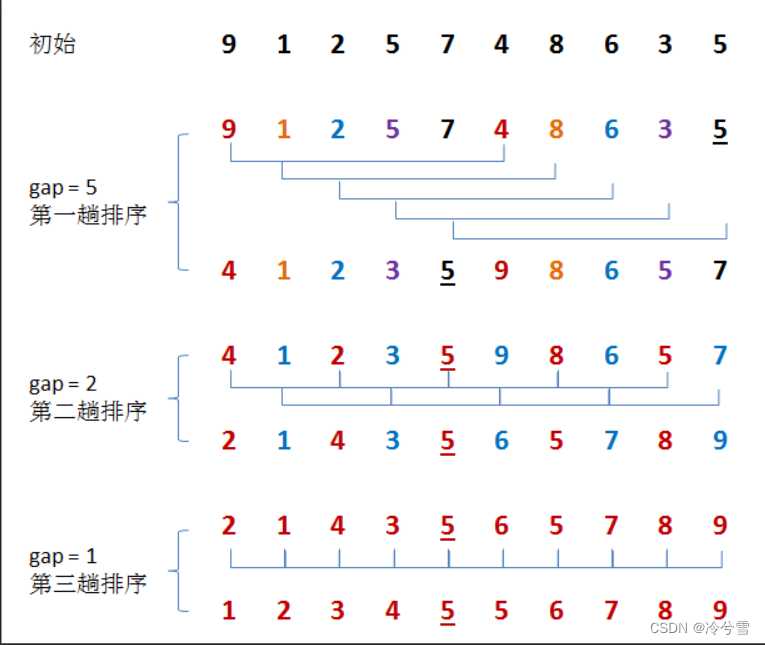
希尔排序的算法流程：

第一遍：分成5组，

第二遍：分成2组，4 3 5 8 5会被进行插入排序

第三遍：gap=1，分成1组，对全部数组进行直接插入排序

def shell_sort(arr):
    # 初始化间隔gap
    gap = len(arr) // 2
    # 开始希尔排序
    while gap > 0:
        # 遍历所有间隔为gap的元素组
        for i in range(gap, len(arr)):
            temp = arr[i]
            j = i
            # 插入排序的思想，对间隔为gap的元素组进行直接插入排序操作
            while j - gap >= 0 and temp < arr[j - gap]:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        # 更新间隔
        gap //= 2
    return arr

# 测试希尔排序函数
example_array = [64, 34, 25, 12, 22, 11, 90]
sorted_array = shell_sort(example_array)
print("排序后的数组：", sorted_array)

堆排序（难）

堆排序（Heap Sort）是一种基于比较的排序算法，它利用堆这种数据结构的特性来进行排序。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

堆排序算法包括两个主要步骤：

建立堆：将无序数组构造成一个最大堆或最小堆。

逐步提取堆顶元素并恢复堆性质：将堆顶元素与最后一个元素交换，然后减少堆的大小，最后调整剩余元素构成的堆，重复这个过程直到堆的大小为1。

def heapify(arr, n, i):
    # 设定最大值索引为i
    largest = i
    # 左子节点索引为2*i+1
    left = 2 * i + 1
    # 右子节点索引为2*i+2
    right = 2 * i + 2

    # 如果左子节点大于根节点
    if left < n and arr[i] < arr[left]:
        largest = left

    # 如果右子节点比最大值还大
    if right < n and arr[largest] < arr[right]:
        largest = right

    # 如果最大值不是根节点
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # 交换
        # 递归地定义子堆
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    # 构建最大堆
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # 一个个从堆顶取出元素
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 交换
        heapify(arr, i, 0)
    return arr

# 测试堆排序函数
example_array = [12, 11, 13, 5, 6, 7]
sorted_array = heap_sort(example_array)
print("排序后的数组：", sorted_array)

归并排序(合并有序序列)

O(nlogn）的时间复杂度，稳定排序

• 把长度为n的输入序列分成两个长度为n/2的子序列；
• 对这两个子序列分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列（这里一次遍历就行了，合并两个有序序列的复杂度是n）

def MergeSort(lst):
    #合并左右子序列函数
    def merge(arr,left,mid,right):
        temp=[]     #中间数组
        i=left          #左段子序列起始
        j=mid+1   #右段子序列起始
        while i<=mid and j<=right:
            if arr[i]<=arr[j]:
                temp.append(arr[i])
                i+=1
            else:
                temp.append(arr[j])
                j+=1
        while i<=mid:
            temp.append(arr[i])
            i+=1
        while j<=right:
            temp.append(arr[j])
            j+=1
        for i in range(left,right+1):    #  !注意这里，不能直接arr=temp,他俩大小都不一定一样
            arr[i]=temp[i-left]
    #递归调用归并排序
    def mSort(arr,left,right):
        if left>=right:
            return
        mid=(left+right)//2
        mSort(arr,left,mid)
        mSort(arr,mid+1,right)
        merge(arr,left,mid,right)

    n=len(lst)
    if n<=1:
        return lst
    mSort(lst,0,n-1)
    return lst

x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in  y:
    arr.append(int(i))
arr=MergeSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
    print(i,end=' ')

计数排序（空间浪费严重）

• 找出待排序的数组中最大和最小的元素；（来建立一个桶）如果这里最大值100，就有100个桶
• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

def CountSort(lst):
    n=len(lst)
    num=max(lst)
    count=[0]*(num+1)
    for i in range(0,n):
        count[lst[i]]+=1
    arr=[]
    for i in range(0,num+1):
        for j in range(0,count[i]):
            arr.append(i)
    return arr

x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in  y:
    arr.append(int(i))
arr=CountSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
    print(i,end=' ')

桶排序（合并多个有序数组）

1、 先分多个桶（可以直接使用n/10这种方法，桶是有序的）

2、在桶内进行排序（任何排序均可）

import java.util.ArrayList;
import java.util.List;
//微信公众号：bigsai
public class test3 {
	public static void main(String[] args) {
		int a[]= {1,8,7,44,42,46,38,34,33,17,15,16,27,28,24};
		List[] buckets=new ArrayList[5];
		for(int i=0;i<buckets.length;i++)//初始化
		{
			buckets[i]=new ArrayList<Integer>();
		}
		for(int i=0;i<a.length;i++)//将待排序序列放入对应桶中
		{
			int index=a[i]/10;//对应的桶号
			buckets[index].add(a[i]);
		}
		for(int i=0;i<buckets.length;i++)//每个桶内进行排序(使用系统自带快排)
		{
			buckets[i].sort(null);
			for(int j=0;j<buckets[i].size();j++)//顺便打印输出
			{
				System.out.print(buckets[i].get(j)+" ");
			}
		}
	}
}

基数排序（Radix Sort）(多轮桶排)

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前

算法实现：

1、取最大值得到最高位

2、从低位到高位，建立桶依次收集和分散，反复几轮之后就是有序的了

算法图解：

下面这段代码实现的很巧妙

1、取最大值得到最高位

2、从低位到高位，建立桶依次收集和分散，反复几轮之后就是有序的了

def radix(arr):

    digit = 0
    max_digit = 1
    max_value = max(arr)
    #找出列表中最大的位数 10^max_digit
    while 10**max_digit < max_value:
        max_digit = max_digit + 1

    while digit < max_digit:
        temp = [[] for i in range(10)] # 二维数组,有10个元素 [[],[],[],..[]]
        for i in arr:
            #求出每一个元素的个、十、百位的值
            t = int((i/(10**digit))%10) # 依次取个位 10位 百位
            temp[t].append(i)

        coll = []
        # 将桶里的东西依次倒出来
        for bucket in temp:
            for i in bucket:
                coll.append(i)

        arr = coll # 此时coll其实已经排过序了
        digit = digit + 1

    return arr

选择排序（有序+无序）

选择排序（select sorting）也是一种简单的排序方法。

基本思想为：

第一次从 arr[0]~arr[n-1] 中选取最小值，与 arr[0] 交换

第二次从 arr[1]~arr[n-1] 中选取最小值，与 arr[1] 交换

第 i 次从 arr[i-1]~arr[n-1] 中选取最小值，与 arr[i-1] 交换

依次类图，总共通过 n - 1 次，得到一个按排序码从小到大排列的有序序列

def selection_sort(arr):
    # 遍历数组中的所有元素
    for i in range(len(arr)):
        # 将当前位置设为最小值位置
        min_index = i

        # 从i+1到数组末尾中找到最小元素的索引
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_index]:
                min_index = j

        # 将找到的最小值交换到它应该在的位置
        arr[i], arr[min_index] = arr[min_index], arr[i]
    return arr

# 测试选择排序函数
example_array = [64, 25, 12, 22, 11]
sorted_array = selection_sort(example_array)
print("排序后的数组：", sorted_array)

总结

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。

不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面

参考文档

1、https://www.cnblogs.com/onepixel/p/7674659.html