重新整理数据结构与算法(c#)—— 平衡二叉树[二十三]

前言

因为有些树是这样子的:

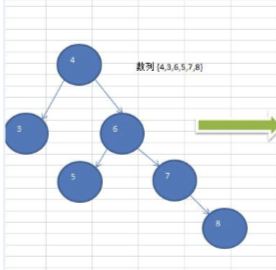
这样子的树有个坏处就是查询效率低，因为左边只有一层，而右边有3层，这就说明如果查找一个数字大于根元素的数字，那么查询判断就更多。

解决方法就是降低两边的层数差距:

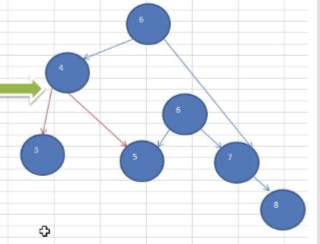
变成这样。

那么如何这样做呢？

如果右边比左边层次大于1，进行左旋转规格:

如果左边比右边层次大于1，进行右旋转:

为什么是这样处理呢?

我拿左旋转来说:

左边是1，右边是3，那么需要右边的给一层给左边。

这时候就是6作为根节点，6作为根节点，本身呢，就是一颗二叉树。

这时候呢，6大于4，所以4在6的右边，而6的左节点肯定大于4（原理的根节点）小于6，所以作为4的左节点代替，4也就成了6的左节点。

右旋转同理。

旋转会出现的问题

就是这样通过右旋转之后，可能达不到目标。

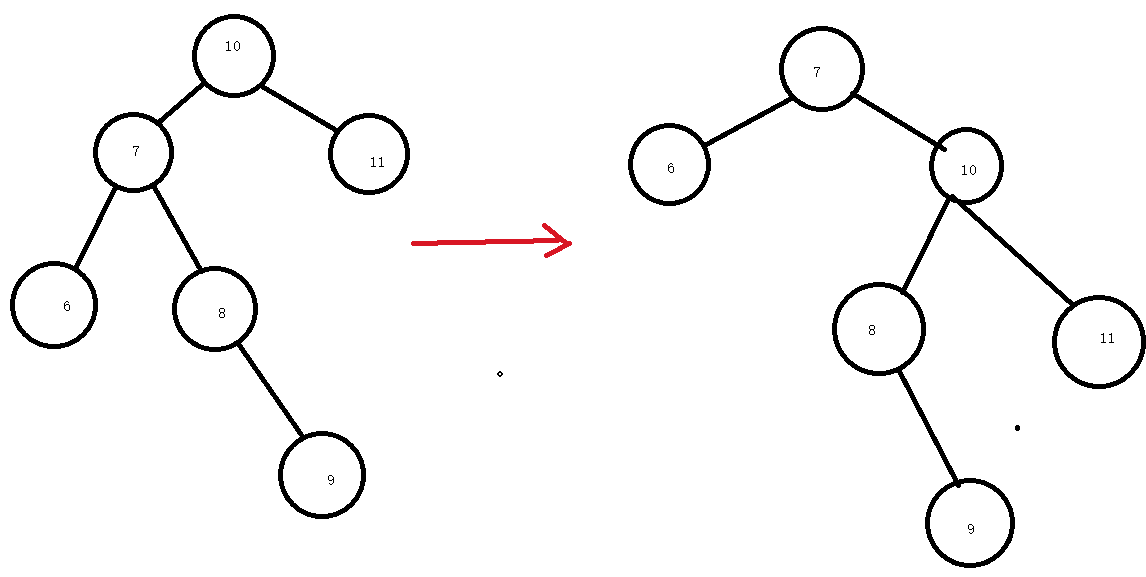
看上面这张图，右旋转后还是不平衡，为什么会这样呢？原因是这样的，我们来看下本质问题，右旋转干了什么？右旋转其实是重新分配元素的过程。

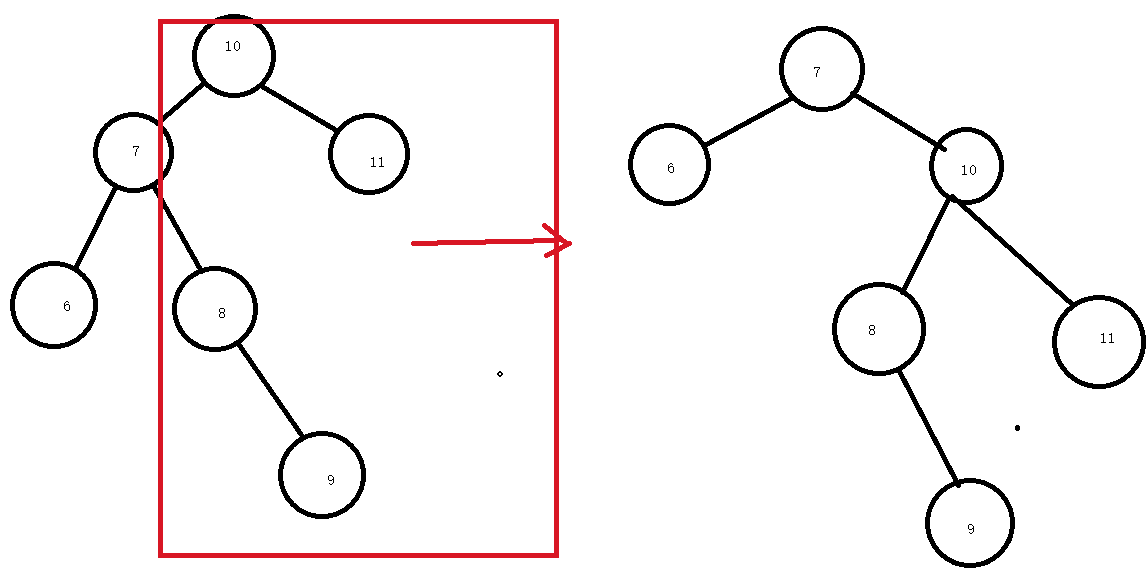
看我这种图红色部分，其实是将红色部门分给了右边，这时候会存在元素个数差异过大的问题。

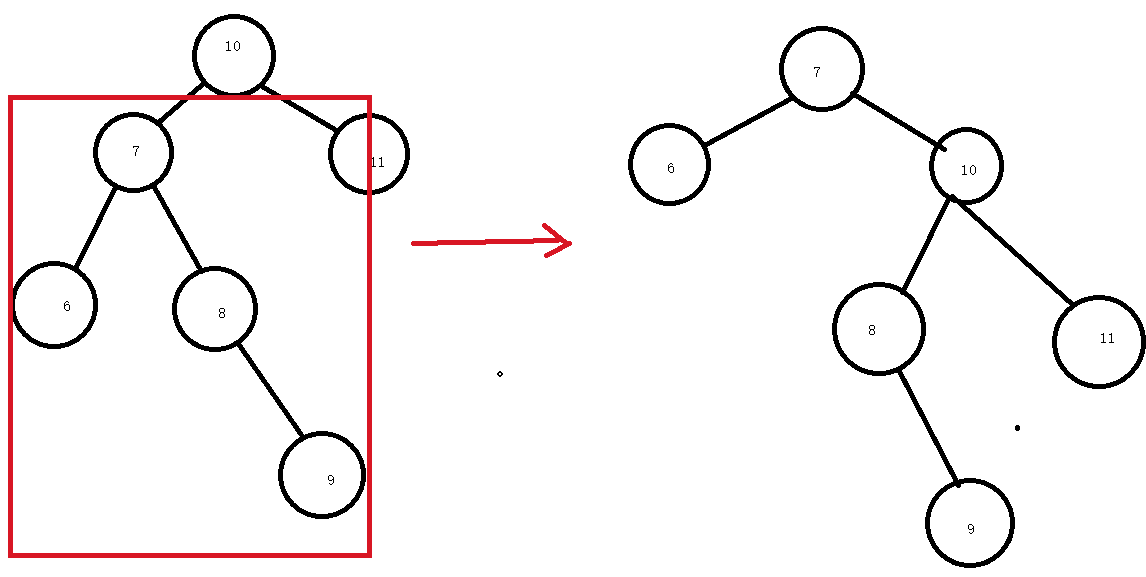
那么这时候该怎么办呢?

要让红框部分进行左旋转才行，那么看代码吧。

正文

节点模型:

public class Node
{
	public Node left;

	public Node right;

	int value;

	public int Value { get => value; set => this.value = value; }

	public Node(int value)
	{
		this.Value = value;
	}
	//中序排序
	public void infixOrder()
	{
		if (this.left != null)
		{
			this.left.infixOrder();
		}
		Console.WriteLine(this);
		if (this.right != null)
		{
			this.right.infixOrder();
		}
	}
	//左子树高度
	public int leftHeight() {
		if (left == null)
		{
			return 0;
		}
		return this.left.height();
	}
	//右子树高度
	public int rightHeight() {
		if (right == null)
		{
			return 0;
		}
		return this.right.height();
	}
	//计算高度
	public int height()
	{
		return Math.Max(left==null?0:this.left.height(),right==null?0:this.right.height())+1;
	}
	//进行左旋转
	private void leftRotate()
	{
		Node newNode = new Node(value);
		newNode.left = left;
		newNode.right = right.left;
		//将右节点变成根节点
		value =right.value;
		//原先右节点被抛弃
		right=right.right;
		//左节点设置为
		left = newNode;
	}
	//进行右旋转
	private void rightRotate()
	{
		Node newNode = new Node(value);
		newNode.left = left.right;
		newNode.right = right;
		value = this.left.value;
		left = left.left;
		right = newNode;
	}
	public override string ToString()
	{
		return Value.ToString();
	}
	//增加元素
	public void addNode(Node node)
	{
		if (node.Value < this.Value)
		{
			if (this.left == null)
			{
				this.left = node;
			}
			else
			{
				this.left.addNode(node);
			}
		}
		else {
			if (this.right == null)
			{
				this.right = node;
			}else {
				this.right.addNode(node);
			}
		}
		if (rightHeight() > leftHeight() + 1)
		{
			if (right.leftHeight() > right.rightHeight())
			{
				right.rightRotate();

			}
			this.leftRotate();
		}
		else if (leftHeight() > rightHeight() + 1)
		{
			if (left.rightHeight() > left.leftHeight())
			{
				left.leftRotate();
			}
			this.rightRotate();
		}
	}
	public Node searchParentNode(int value)
	{
		if ((this.left != null && this.left.value == value || (this.right != null && this.right.value == value)))
		{
			return this;
		}
		else
		{
			if (this.value < value && this.left != null)
			{
				return this.left.searchParentNode(value);
			}
			else if (this.value >= value && this.right != null)
			{
				return this.right.searchParentNode(value);
			}
			else
			{
				return null;
			}
		}
	}
	//查找元素
	public Node searchNode(int value)
	{
		if (this.Value == value)
		{
			return this;
		}
		if (this.Value > value)
		{
			if (this.left != null)
			{
				return this.right.searchNode(value);
			}
			else
			{
				return null;
			}
		}
		else
		{
			if (this.left != null)
			{
				return this.left.searchNode(value);
			}
			else
			{
				return null;
			}
		}
	}
}

树模型:

public class BinarySortTree
{
	//根节点
	Node root;

	internal Node Root { get => root; set => root = value; }

	public BinarySortTree(Node root)
	{
		this.Root = root;
	}

	public BinarySortTree() : this(null)
	{

	}

	public void add(Node node)
	{
		if (Root == null)
		{
			Root = node;
		}
		else
		{
			this.Root.addNode(node);
		}
	}

	public void infixOrder()
	{
		if (Root == null)
		{
			Console.WriteLine("root 为空");
		}
		else
		{
			Root.infixOrder();
		}
	}

	public Node searchNode(int value)
	{
		if (Root==null)
		{
			Console.WriteLine("root 为空");
		}
		return Root.searchNode(value);
	}

	public int delRightTreeMin(Node node)
	{
		Node tagert = node;
		while (tagert.left!=null)
		{
			tagert = tagert.left;
		}
		delNode(tagert.Value);
		return tagert.Value;
	}

	public Node searchParentNode(int value)
	{
		if (Root != null)
		{
			return Root.searchParentNode(value);
		}
		return null;
	}

	public void delNode(int value)
	{
		if (Root == null)
		{
			return;
		}
		Node node=searchNode(value);
		if (node == null)
		{
			return;
		}
		if (node.Value == Root.Value)
		{
			Root = null;
			return;
		}
		Node parent = searchParentNode(value);
		if (node.left == null && node.right == null)
		{
			if (parent.left.Value == value)
			{
				parent.left = null;
			}
			else
			{
				parent.right = null;
			}
		}
		else if (node.left != null && node.right != null)
		{
			 //删除左边最大值或者右边最小值,然后修改值为删除的值
			 parent.right.Value=delRightTreeMin(node.right);
		}
		else
		{
			if (node.left != null)
			{
				if (parent.left.Value == value)
				{
					parent.left = node.left;
				}
				else
				{
					parent.right = node.left;
				}
			}
			else {
				if (parent.left.Value == value)
				{
					parent.left = node.right;
				}
				else
				{
					parent.right = node.right;
				}
			}
		}
	}
}

测试代码:

static void Main(string[] args)
{
	int[] arr = { 10, 11, 7, 6, 8, 9 };
	BinarySortTree binarySortTree = new BinarySortTree();
	//循环的添加结点到二叉排序树
	for (int i = 0; i < arr.Length; i++)
	{
		binarySortTree.add(new Node(arr[i]));
	}
	//中序遍历后的数据
	Console.WriteLine("树的高度=" + binarySortTree.Root.height()); //3
	Console.WriteLine("树的左子树高度=" + binarySortTree.Root.leftHeight()); // 2
	Console.WriteLine("树的右子树高度=" + binarySortTree.Root.rightHeight()); // 2
	Console.WriteLine("当前的根结点=" + binarySortTree.Root);//8
	Console.Read();
}

结果: