9. Complex Vectors and Matrices

9.1 Real versus Complex

R= line of all real numbers ($-\infty < x < \infty$) $\longleftrightarrow$ C=plane of all complex numbers $z=x+iy$
|x| = absolute value of x $\longleftrightarrow$ $|z| = \sqrt{x^2+y^2} = r$ = absolute value (or modulus) of z
1 and -1 solve $x^2=1$ $\longleftrightarrow$ $z=1,w,...,w^{n-1}$ solve $z^n=1$ where $w = e^{2\pi i/n}$
$R^n$ : vectors with n real components $\longleftrightarrow$ $C^n$: vectors with n complex components
length : $||x||^2 = x_1^2 + \cdots + x_n^2$ $\longleftrightarrow$ $||z||^2 = |z_1|^2 + \cdots + |z_n|^2$
transpose : $A_{ij}^T = A_{ji}$ $\longleftrightarrow$ conjugate transpose $A_{ij}^H = \overline{A_{ji}}$
dot/inner product : $x^Ty = x_1y_1 + \cdots + x_ny_n$ $\longleftrightarrow$ dot/inner product : $u^Hv = \overline{u_1}v_1 + \cdots + \overline{u_n}v_n$
reason for $A^T$ : $(Ax)^Ty = x^T(A^Ty)$ $\longleftrightarrow$ reason for $A^H$: $(Au)^Hv = u^H(A^Hv)$
orthgonality : $x^Ty = 0$ $\longleftrightarrow$ orthgonality : $u^Hv = 0$
symmetric matrices: $S=S^T$ $\longleftrightarrow$ Hermitian matrices: $S=S^H$
skew-symmetric matrices : $K^T = K^{-1}$ $\longleftrightarrow$ skew-Hermitian matrices : $K^H = -K$
orthgonal matrices : $Q^T = Q^{-1}$ $\longleftrightarrow$ unitary matrices : $U^H = U^{-1}$
orthonormal matrices : $Q^TQ = I$ $\longleftrightarrow$ orthonormal matrices : $U^HU = I$
$S = Q\Lambda Q^{-1} = Q\Lambda Q^T$ $\longleftrightarrow$ $S = U\Lambda U^{-1} = U\Lambda U^H$
$(Qx)^T(Qy)= x^Ty$ and $||Qx|| = ||x||$ $\longleftrightarrow$ $(Ux)^H(Uy)= x^Hy$ and $||Uz|| = ||z||$

9.2 Complex Numbers

Complex numbers correspond to points in a plane. Real numbers go along the x axis.Pure imaginary numbers are on the y axis. The complex number $a+bi$ is at the point with coordinates (a, b).

Keys:

Add : $(a + bi) + (c + di) = (a+c)+(b+d)i$
Multiply : $(a+bi)(a-bi)=a^2+b^2$
Eigenvalues $\lambda$ 和 $\overline{\lambda}$ : If $Ax=\lambda x$ and A is real then $A\overline{x}=\overline{\lambda}\overline{x}$
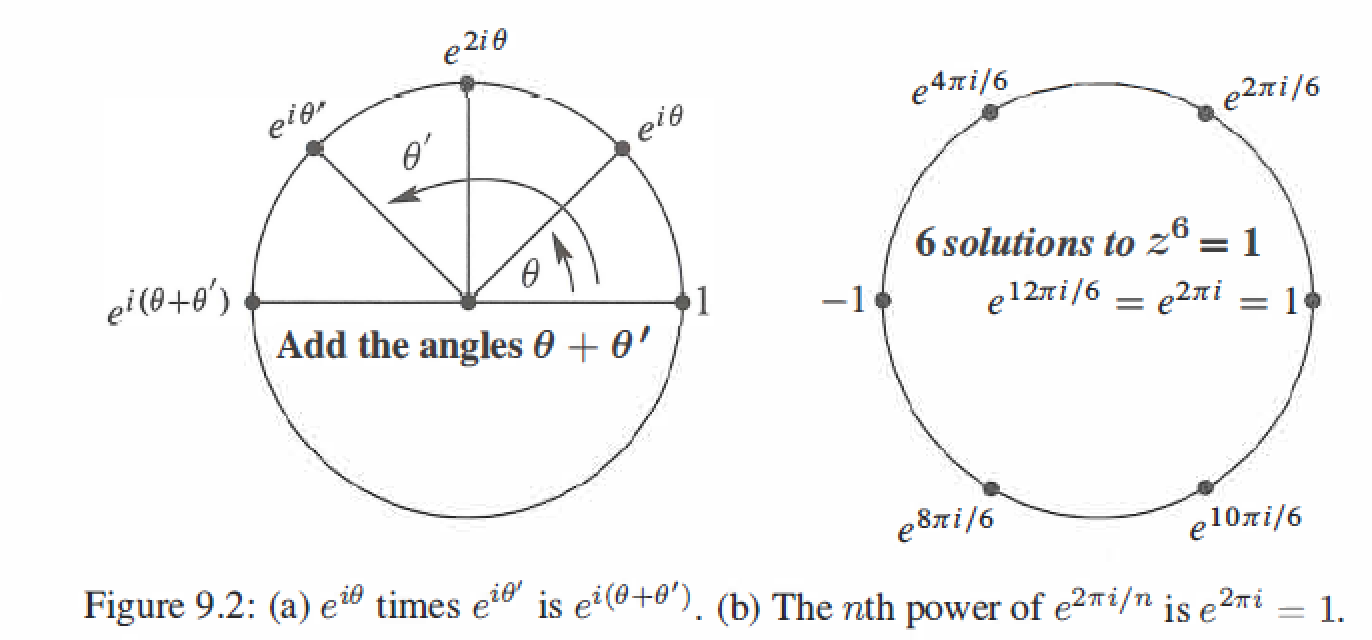
Euler's Formula : $e^{i\theta}= cos\theta + isin\theta$
Polar Form : The number $z=a+ib$ is also $z=rcos\theta + irsin\theta = re^{i\theta} \ \ with \ \ r = |z| = \sqrt{a^2 + b^2}$
Powers: The nth power of $z=r(cos\theta+isin\theta)$ is $z^n=r^n(cos(n\theta)+isin(n\theta))$
The nth roots of 1 : Set $w=e^{2\pi i/n}$, the nth powers of $1,w,w^2,...,w^{n-1}$ all equal 1, they solve the equation $z^n=1$

9.3 Hermitian and Unitary Matrices

When we transpose a complex vector z or matrix A , also take the complex conjugate too.

With $z_j = a_j + i b_j$:

conjugate transpose : $\overline{z}^T=[\overline{z_1} \cdots \overline{z_n}] = [a_1 - ib_1 \cdots a_n - ib_n]$

length squared : $[\overline{z_1} \cdots \overline{z_n}] \left[ \begin{matrix} z_1 \\ \vdots \\ z_n\end{matrix}\right]= |z_1|^2 + \cdots + |z_n|^2 \longleftrightarrow \overline{z}^Tz=z^Hz = ||z||^2$ ($z^H$ is z Hermitian)

Inner product : $u^{H}v = [\overline{u_1} \cdots \overline{u_n}] \left[ \begin{matrix} v_1 \\ \vdots \\ v_n\end{matrix}\right]= \overline{u_1}v_1 + \cdots + \overline{u_n}v_n$

Hermitian Matrix

Among complex matrices, with Hermitian matrices : $S=S^H， s_{ij} = \overline{s_{ji}}$

\[S = \left[ \begin{matrix} 2&3-3i \\ 3+3i&5 \end{matrix} \right] \\
S^H = \left[ \begin{matrix} 2&3+3(-i) \\ 3-3(-i)&5 \end{matrix} \right] = \left[ \begin{matrix} 2&3-3i \\ 3+3i&5 \end{matrix} \right] = S \\
\]

Eigenvalues of a Hermitian matrix is real, and eigenvectors of a Hermitian are orthogonal.

Unitary Matrices

A unitary matrix Q is a complex square matrix that has orthonormal columns.

Unitary matrix that diagonalizes S : $Q=\frac{1}{\sqrt{3}}\left[ \begin{matrix} 1&1-i \\ 1+i&-1 \end{matrix}\right]$

Orthonormal columns : $Q^HQ=I$

Square + Orthonormal columns = Unitary matrix : $Q^{H} = Q^{-1}$

If Q is unitary the $||Qz||=||z||$. Therefore $Qz=\lambda z$ leads to $|\lambda| = 1$

9.4 The Fast Fourier Transform

Fourier Matrix

\[F_n = \left [ \begin{matrix} 1&1&\cdots&1 \\ 1&w^1&\cdots&w^{n-1} \\ 1&w^2&\cdots&w^{2(n-1)}\\ \vdots&\vdots&\vdots&\vdots \\ 1&w^{n-1}&\cdots&w^{(n-1)^2}\end{matrix} \right] \\
(F_n)_{ij} = w^{ij}, (i,j=0,1,2,...,n-1) \\
w_n = e^{2\pi / n * i} \\
w_n = e^{\pi / 2 * i} = i, w_n = e^{\pi * i} = -1 \\
w_n = e^{3\pi / 2 * i} = -i, w_n = e^{2\pi * i} = 1
\]

example:

$F_4$ is orthogonal and symmetric.

\[F_4 = \left [ \begin{matrix} 1&1&1&1 \\ 1&w_4^1&w_4^{2}&w_4^{3} \\ 1&w_4^2&w_4^{4}&w_4^{6}\\ 1&w_4^{3}&w_4^{6}&w_4^{9}\end{matrix} \right] =
\left [ \begin{matrix} 1&1&1&1 \\ 1&i&-1&-i \\ 1&-1&1&-1\\ 1&-i&-1&i\end{matrix} \right]
\\

\left [ \begin{matrix} &&& \\ &F_2&& \\ &&& \\ &&&F_2\end{matrix} \right] =
\left [ \begin{matrix} 1&1&& \\ 1&i^2&& \\ &&1&1\\ &&1&i^2\end{matrix} \right]
\\
\Downarrow \\

F_4 =
\left [ \begin{matrix} 1&1&1&1 \\ 1&w_4^1&w_4^{2}&w_4^{3} \\ 1&w_4^2&w_4^{4}&w_4^{6}\\ 1&w_4^{3}&w_4^{6}&w_4^{9}\end{matrix} \right] =
\left [ \begin{matrix} 1&&1& \\ &1&&i \\ 1&&-1&\\ &1&&-i\end{matrix} \right]

\left [ \begin{matrix} 1&1&& \\ 1&i^2&& \\ &&1&1\\ &&1&i^2\end{matrix} \right]

\left [ \begin{matrix} 1&&& \\ &&1& \\ &1&& \\ &&&1 \end{matrix} \right] \\
\]

$w_4 = e^{\pi / 2 * i} \\
F_4^{H}F_4 = I, \ \ F^{-1}_4 = \frac{1}{4}\overline{F}_4$

The key idea is to connect $F_n$ with the half-size Fourier matrix $F_{n/2}$, and keep going to $F_{n/4}$，which can be factored in a way that procdeces many zeros, and improve multiply quickly.

Save more than half of time : $n^2 \Rightarrow 1/2 n log_2^n$

\[F_{64} = \left[ \begin{matrix} I_{32}&D_{32} \\ I_{32}&-D_{32} \end{matrix}\right]
\left[ \begin{matrix} F_{32}&0 \\ 0&F_{32} \end{matrix}\right]
\left[ \begin{matrix} P_{64} \end{matrix}\right] \\

=\left[ \begin{matrix} \left[ \begin{matrix} I_{16}&D_{16} \\ I_{16}&-D_{16} \end{matrix}\right]&0 \\ 0& \left[ \begin{matrix} I_{16}&D_{16} \\ I_{16}&-D_{16}\end{matrix}\right] \end{matrix}\right]

\left[ \begin{matrix} \left[ \begin{matrix} F_{16}&0 \\ 0&F_{16} \end{matrix}\right]&0 \\ 0& \left[ \begin{matrix} F_{16}&0 \\ 0&F_{16} \end{matrix}\right] \end{matrix}\right]

\left[ \begin{matrix} P_{32}& \\ &P_{32} \end{matrix}\right] \\
D = \left[ \begin{matrix} 1&&& \\ &w^1&& \\ &&\ddots& \\ &&&w^n \end{matrix}\right] \\
P = \left [ \begin{matrix} even-odd \\ permutation \end{matrix}\right]
\]