Fisher线性判别分析(二分类)
LDA(Linear Discriminant Analysis)是一种经典的线性判别方法,又称Fisher判别 分析。该方法思想比较简单:给定训练集样例,设法将样例投影到一维的直线 上,使得同类样例的投影点尽可能接近和密集,异类投影点尽可能远离。
核心问题:找到线性系数向量
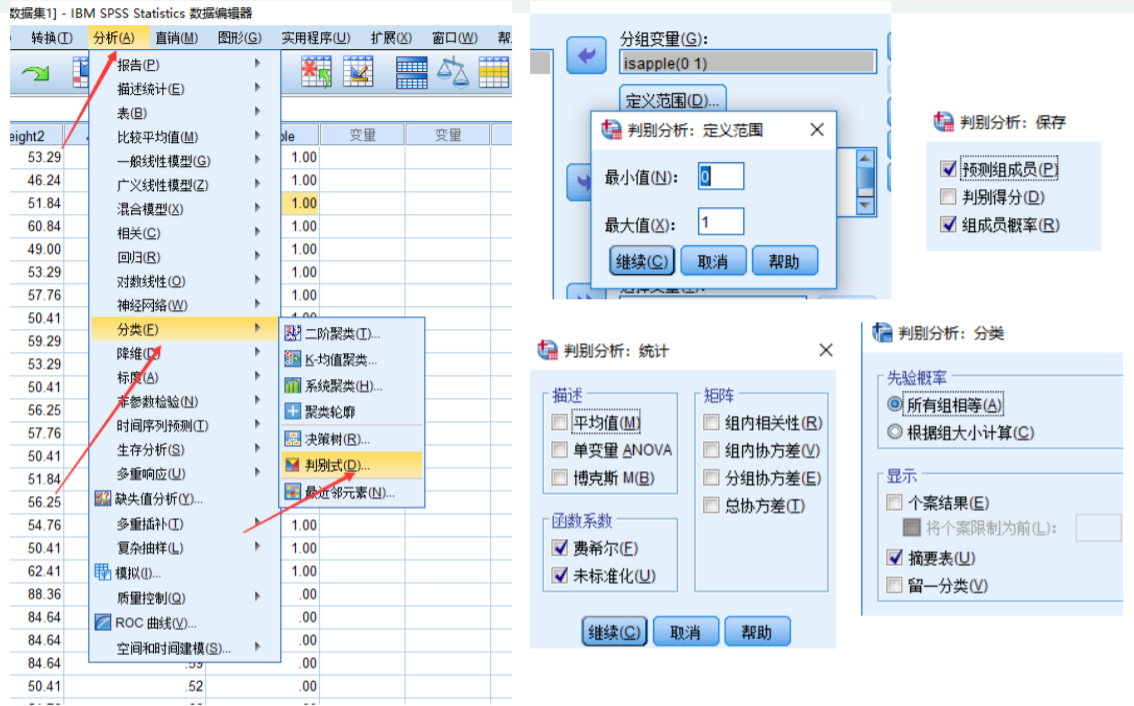
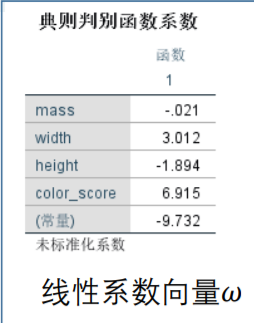
结果分析

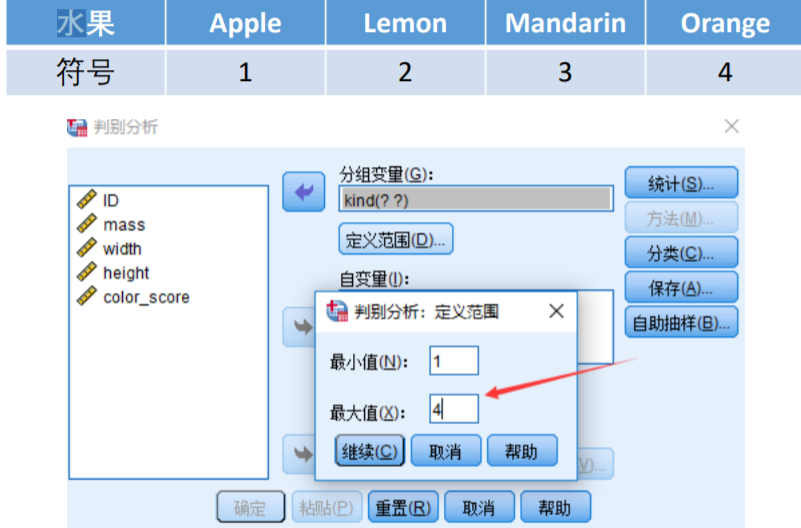
Fisher判别分析可用于多分类
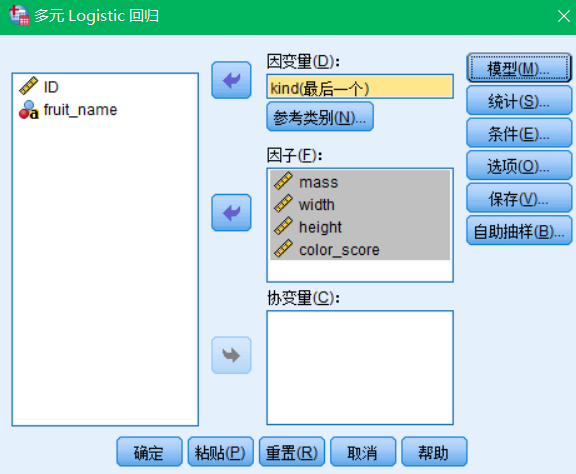
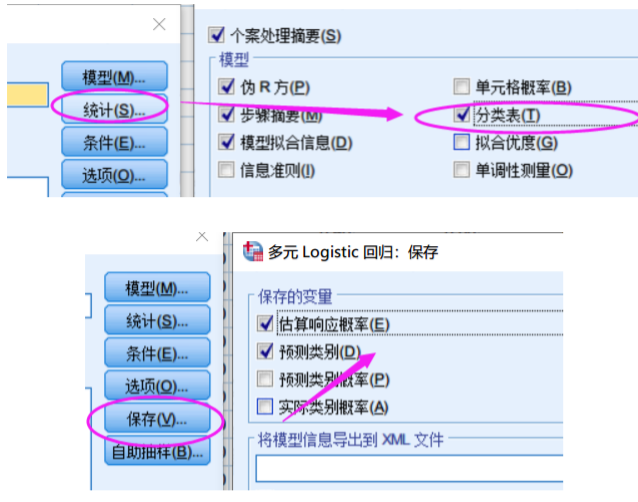
Logistic回归也可用于多分类

Fisher线性判别分析(二分类)的更多相关文章
- Fisher线性判别分析
Fisher线性判别分析 1.概述 在使用统计方法处理模式识别问题时,往往是在低维空间展开研究,然而实际中数据往往是高维的,基于统计的方法往往很难求解,因此降维成了解决问题的突破口. 假设数据存在于d ...
- 主成分分析(PCA)与线性判别分析(LDA)
主成分分析 线性.非监督.全局的降维算法 PCA最大方差理论 出发点:在信号处理领域,信号具有较大方差,噪声具有较小方差 目标:最大化投影方差,让数据在主投影方向上方差最大 PCA的求解方法: 对样本 ...
- 线性判别分析(LDA)准则:FIsher准则、感知机准则、最小二乘(最小均方误差)准则
准则 采用一种分类形式后,就要采用准则来衡量分类的效果,最好的结果一般出现在准则函数的极值点上,因此将分类器的设计问题转化为求准则函数极值问题,即求准则函数的参数,如线性分类器中的权值向量. 分类器设 ...
- 线性判别分析(Linear Discriminant Analysis)转载
1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...
- 线性判别分析算法(LDA)
1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...
- (数据科学学习手札17)线性判别分析的原理简介&Python与R实现
之前数篇博客我们比较了几种具有代表性的聚类算法,但现实工作中,最多的问题是分类与定性预测,即通过基于已标注类型的数据的各显著特征值,通过大量样本训练出的模型,来对新出现的样本进行分类,这也是机器学习中 ...
- 机器学习理论基础学习3.2--- Linear classification 线性分类之线性判别分析(LDA)
在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题 ...
- matlab 实现感知机线性二分类算法(Perceptron)
感知机是简单的线性分类模型 ,是二分类模型.其间用到随机梯度下降方法进行权值更新.参考他人代码,用matlab实现总结下. 权值求解过程通过Perceptron.m函数完成 function W = ...
- 线性判别分析(LDA), 主成分分析(PCA)及其推导【转】
前言: 如果学习分类算法,最好从线性的入手,线性分类器最简单的就是LDA,它可以看做是简化版的SVM,如果想理解SVM这种分类器,那理解LDA就是很有必要的了. 谈到LDA,就不得不谈谈PCA,PCA ...
- 机器学习中的数学-线性判别分析(LDA), 主成分分析(PCA)
转:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html 版权声明: 本文由L ...
随机推荐
- CKS 考试题整理 (06)-默认网络策略
Context 一个默认拒绝(default-deny)的NetworkPolicy可避免在未定义任何其他NetworkPolicy的namespace中意外公开Pod. Task 为所有类型为Ing ...
- DevOps|中式土味OKR与绩效考核落地与实践
昨天一个小伙伴和我讨论了一下OKR和绩效管理,所以这次想简单明了地说下在中国怎么做比较合适,很多高大上的理论无法落地也是空中楼阁. 首先说一些,我个人的理解 道德品质和能力素质决定了一个人的职位行为 ...
- Kubernetes(k8s)访问控制:身份认证
目录 一.系统环境 二.前言 三.Kubernetes访问控制 四.身份认证简介 五.身份认证 5.1 配置客户端机器 5.2 使用base auth的方式进行认证 5.3 使用token的方式进行认 ...
- Auto.js食用指南
Auto.js食用指南 控件点击是autojs特有的一项功能,基于安卓的无障碍功能的,在软件上有很好的支持,常用于办公软件等...... 前言: 软件选择: auto.js 8.0pro版本(对比4. ...
- YOLOX目标检测实战:LabVIEW+YOLOX ONNX模型实现推理检测(含源码)
目录 前言 一.什么是YOLOX 二.环境搭建 1.部署本项目时所用环境: 2.LabVIEW工具包下载及安装: 三.模型的获取与转化[推荐方式一] 1.方式一:直接在官网下载yolox的onnx模型 ...
- js将数字金额转换成中文金额格式
在开发中我们经常会遇到处理数字的问题,下面介绍一种处理数字金额转换为中文金额的方式: 我们通常使用三种书面数字系统:全球使用的阿拉伯数字系统和两种本地数字系统(繁体.简体).常规时我们使用阿拉伯数字( ...
- C# 处理 csv 文件中的双引号
C# CSV 双引号处理 直接上代码,自己写的,有问题可以随时联系 // 没有保证所有的都能对上,目前只处理了自己所遇见的格式 public static string[] SplitStr(stri ...
- Nginx报错:nginx: [error] OpenEvent("Global\ngx_reload_14944") failed (2: The system cannot find the file specified)
nginx.exe -s reload 执行报错 错误原因: Nginx 尚未启动导致,执行 start nginx 命令开启Nginx nginx.exe -s reload 至此问题解决
- CGLIB动态代理对象GC问题排查
一.问题是怎么发现的 最近有个新系统开发完成后要上线,由于系统调用量很大,所以先对核心接口进行了一次压力测试,由于核心接口中基本上只有纯内存运算,所以预估核心接口的压测QPS能够达到上千. 压测容器配 ...
- 零基础入门——从零开始学习PHP反序列化笔记(一)
靶场环境搭建 方法一:PHPstudy搭建 GitHub地址 https://github.com/mcc0624/php_ser_Class 方法二:Docker部署 pull镜像文件 docker ...
