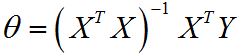cs 保研经验贴 | 数学试题 · 自动化所特供版
据(2022 年我所看的)往年经验,自动化所比较重视数学。
感觉,按照自动化所的数学题库复习,就足以应付大多数夏令营的笔试面试了。
同站相关博客:
- cs 保研经验帖 | 综合面试题库
- cs 保研经验帖 | 英语口试
- 线性代数 | 等价 · 相似 · 合同
- 线性代数 | 最小二乘法的直观理解
- 高等数学 | 数列 函数 级数 函数项级数之收敛性(上)
- 高等数学 | 数列 函数 级数 函数项级数之收敛性(下)
高等数学
初等函数的定义:
- 幂函数、指数函数、对数函数、三角函数、反三角函数,与常数经过有限次的有理运算(加、减、乘、除、有理数次乘方、有理数次开方),及有限次函数复合的函数。并且能用一个解析式表示。
反函数存在条件:
- 定义域 值域 一一映射。
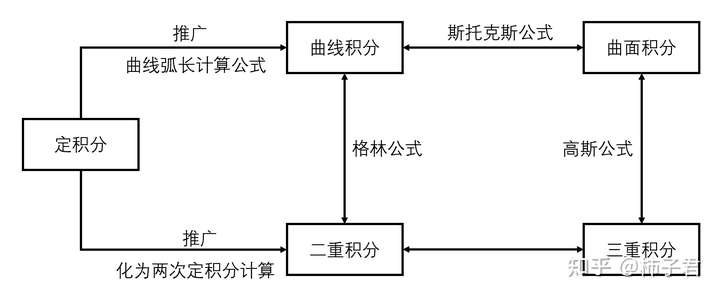
二次积分和二重积分的区别和联系:
- 没有本质区别。将二重积分化为二次积分(不一定能),是为了好算。
- 二重积分:二元函数在空间上的积分,求曲顶柱体体积。
- 二次积分:两次单变量积分,就是平常计算时,一个变量一个变量积分、
green 公式,gauss 公式,stokes 公式,条件 关联
- 条件:闭区域面 / 体 / 光滑曲面带边界,连续 且 一阶连续偏导数。
- green: Qx - Py,
- gauss: Px + Qy + Rz,
- stokes:
- 关系:
数列和函数极限的定义:
- 数列极限:若存在 A,使得任意 ε 存在 N,n>N → |a_n-A|<ε,则 lim a_n=A
- 函数极限:若存在 A,使得任意 ε 存在 δ,|x1-a|<δ → |f(x1)-A|<ε,则 lim f(a)=A
什么是连续、可导 / 可微。
- 连续:某点连续:极限值=函数值(不会跳变),函数连续:每个点都连续。
- 一致连续:对区间 I 上任意两点 x1 x2,任意 ε 存在 δ,|x1-x2|<δ → |f(x1)-f(x2)|<ε。不能陡到难以接受。闭区间上 连续 等价于 一致连续。
- 可微:若自变量在点x的改变量 Δx(可能是向量),与函数相应的改变量Δy,有关系Δy=A·Δx+ο(Δx),其中A与Δx无关。那么 A 是微分。
- 可导:lim Δy/Δx =A 存在,那么 A 是导数。两侧可导 → 连续,单侧可导 另一侧可跳变。
- 方向导数:lim f(x+Δx, y+Δy) / sqrt(Δx²+Δy²) =A 存在,那么 A 是导数。
可微 可导 连续 关系
- 一元:可微 = 可导 > 连续 > 可积。
- 多元:
- 偏导数 在邻域 存在且连续 → 可微;
- 可微 > 偏导数存在,两边偏导数 → 连续,一边偏导数 不一定 连续。
Riemann 积分的概念:
- 黎曼可积:如果函数 f 在闭区间 [a,b] 上,无论怎样进行分割,只要 子区间长度最大值 足够小,黎曼和都趋向于一个确定值,那么在闭区间 [a,b] 上的黎曼积分存在 = 黎曼和的极限。
- 任意 ε 存在 δ,子区间长度最大值 λ<δ 时,\(|\sum_{i=1}^{n-1}f(t_i)(x_{i+1}-x_i)|-S<\epsilon\) 。
- 可验证的定义,达布积分:任意 ε 存在 分割,使得任何更精细的分割都 |Σ|-S<ε。
Lebesgue 积分的概念(没学过,不太会)。
如何求带条件的极值,lagrange 乘数法:
- z=f(x,y) 当 φ(x,y)=0 时的极值,构造 lagrange 函数 L(x,y,λ) = f(x,y) + λφ(x,y)。
- 求 L 的驻点,即 x y λ 偏导数 = 0,即得。
介值定理,零点存在定理,最值定理:
- 介值定理:设函数
是
上的连续函数,且存在不等式
,则必然至少一个数
,能够使得
。
- 零点存在定理:设函数是
上的连续函数,且存在不等式
,则在
上,至少存在一个数
,能够使得
成立。
- 最大值最小值定理:设函数
为
上的连续函数,则
必然在
上存在最大值
和最小值
。
- 介值定理:设函数
积分中值定理:
- 条件:闭区间 / 有界闭区域 连续。
- 第一:存在 ε∈[a,b] 使得
- 第二:f 在 [a,b] 可积(不一定连续),g 在 [a,b] 上单减 且 ≥ 0,存在 ξ∈[a,b]
,还有一个单增形式。
微分中值定理:lagrange,cauchy,Rolle,区别 联系 条件
- 条件:闭区间连续,开区间可导。
- Rolle: f(a)=f(b) 则 f'(ξ)=0。
- lagrange: f'(ξ) = (f(b)-f(a)) / (b-a)
- cauchy: f'(ξ)/g'(ξ) = (f(b)-f(a)) / (g(b)-g(a))
- 联系:是 推广 & 特殊情况 的关系。
洛必达法则 L' Hospital:
0/0 ∞/∞ 上下求导。
条件:
- x → a 时 f 和 F 都 → 0,在 a 的去心邻域里 f' F' 都存在 且 F' ≠ 0,lim f' / F' 存在(或为无穷大)。
- x → ∞ 时 f 和 F 都 → 0,当 |x|>N 时 f' F' 都存在 且 F' ≠ 0,lim f' / F' 存在(或为无穷大)。
解析式:\(lim_{x\rarr a} f(x)/F(x)=lim_{x\rarr a} f'(x)/F'(x)\) 。
理解:局部切线代替函数曲线。
泰勒公式:
 ,方法是 拿待定系数多项式近似,求导 LHS=RHS 求待定系数。
,方法是 拿待定系数多项式近似,求导 LHS=RHS 求待定系数。- piano 余项:o[(x-x0)^n] 是 (x-x0)^n 的高阶无穷小,lagrange 余项
。
- 泰勒级数收敛:充要:泰勒展开幂级数收敛(看收敛域),且 某一数的邻域里,展开阶数 → 无穷,lagrange 余项 → 0。
代数基本定理:
- n次复系数多项式方程,在复数域内有且只有n个根(重根按重数计算)。
牛顿迭代法:
- 求解函数零点:借助泰勒级数,从初始值开始,快速向零点逼近。
- 找一点 x,做斜率为导数的切线,更新 x = 切线与 x 轴交点。

- 收敛条件:f(x) 充分光滑(各阶导数存在且连续),f'(a) ≠ 0(单重零点)则初始值在 a 的某个邻域里 收敛速度二阶,f'(a) = 0(多重零点)收敛速度一阶。
- x 阶收敛:第 k 次迭代绝对误差为 ek,
,若 p=2 则二阶收敛。
- 缺点:函数光滑严苛,初始值必须尽量靠近最终解。
线性代数
向量空间 / 线性空间:
- 某集合里定义了 向量加法 数乘 运算,集合对 加法 数乘 封闭。
- 加法满足:交换律 α+β=β+α,结合律 α+(β+γ)=(α+β)+γ,零元 α+0=α 逆元 α+β=0 β=-α。
- 乘法满足:单位元 1α=α,结合律 (kl)α=k(lα),和向量加法的两个分配律 (k+l)α=kα+lα k(α+β)=kα+kβ。
线性相关 & 线性无关:
- 对线性空间 V 里的向量 v1, v2, ..., vn,存在不全为零的 c1, c2, ..., cn,使得 c1v1+ c2v2+ ... + cnvn = 0,那么 v1, v2, ..., vn 线性相关。如果不存在 不全为零的 c 则线性无关。
- 线性相关:列向量组成矩阵 行秩不满,可以用一堆东西的线性组合表示另一个。
- 线性无关:广义 组成的四边形 六面体 超几何体 体积不为零。
- 极大线性无关组:在某线性空间中,拥有向量个数最多的 线性无关向量组。
矩阵的秩 Matrix Rank,物理意义,相关的性质:
线性无关向量的个数,最大 行列式 ≠ 0 子式的维度。
定义的相互转化(等价性):
- r 阶 行列式 ≠ 0 子式,这 r 个向量线性无关。
- 若取 r+1 阶子式,这些行 / 列向量必然线性相关,则行列式 = 0。
性质:
- 基础:初等变换不改变秩,乘可逆矩阵不改变秩,矩阵可逆 <=> 矩阵满秩
- 高级:
- r(A) + r(B) - n ≤ r(AB) ≤ min{r(A), r(B)},(分块矩阵)
- max{r(A), r(B)} ≤ r(A, B) ≤ r(A) + r(B),(感性理解)
- A B 相似则 r(A)=r(B)。
物理意义:把矩阵看作变换,变换后,虽然没法完全不丢信息(不满秩),但至少还能保住几个面(秩)。
矩阵的迹 trace,相关的性质:
- 所有对角元的和,也是所有特征值的和。
- tr(AB) = tr(BA),tr(mA+nB) = m tr(A) + n tr(B),线性 可乘。
- d tr(A) = tr(dA)
线性方程组 Ax = b 有解 / 无解 / 有唯一解 的条件:
- 有解:b 存在于 A 的列向量的线性空间,b 能被 A 的列向量线性表示,A 的秩 = 分块矩阵 (A,b) 的秩
- 多解 / 唯一解:A 的列向量线性无关(列满秩),唯一解;Ax=0 列满秩,则只有零解。非列满秩,则多解。
- (系数矩阵 / 增广矩阵)
矩阵的特征值是什么,有什么物理意义,应用
- Ax=λx。算子的本征值(投影不变,有点像傅里叶变换 卷积指数信号还是指数信号)。
- —个变换矩阵的所有特征向量,都是正交的,组成了这个变换矩阵的一组基。
- 矩阵的特征值分解:\(A=Q\Sigma Q^{-1}\),Σ是对角阵,Q是特征列向量组成的矩阵。
- 怎么求:
- 写出方程丨λE-A丨=0,其中I为与A同阶的单位阵,λ为代求特征值
- 将n阶行列式变形化简,得到关于λ的n次方程
- 解此n次方程,即可求得A的特征值
- 应用:PCA 主成分分析。
初等变换:
- 用一非零的数乘以某一 行 / 列,把一 行 / 列 的倍数加到另一 行 / 列,互换两 行 / 列 的位置。
- 初等矩阵:单位矩阵 E 经过一次初等变换。
- 矩阵 上三角 下三角:
- 行列式为对角线元素相乘。直接初等变换即可得到。
矩阵的恒等变换:
- 就是单位矩阵。
奇异矩阵:
- 行列式 = 0 的方阵,非满秩 的方阵。
伴随矩阵:
矩阵对角化:
特征值特征向量 判断能否对角化:
- 所有特征值都不相等:ok。
- 重数为 k 的特征值 也有 k 个特征向量:ok。小于 k 则不行。
对角化的方法:
- 特征值求出来,然后特征向量组成的矩阵 单位正交化,最后 Σ = T'AT。
正交矩阵:
- \(AA^T=A^TA=E\)。
- \(A^T=A^{-1}\) 也是正交矩阵,行向量 列向量 是 单位向量 且两两正交,|A|=1 或 -1(显然)。行向量 / 列向量 是 规范正交基。
- 左乘正交矩阵造成的空间变换,是用一个新空间代替原有空间,即用另一组正交基描述被变换的向量,不改变原向量的长度和空间位置。
矩阵的 等价,相似,合同:
- 相似:P^{-1}AP=B,则 A B 相似。
- 条件:
- 充要:两矩阵有相同的 行列式,不变因子,初等因子组。
- 充要:相同的 Jordan 标准型(除 Jordan 块排列次序)。
- 必要(相似能推出以下):行列式,秩,迹,特征多项式 一样。。
- 相似对角化:与对角阵相似,当且仅当 A 有 n 个线性无关的特征向量。
- 施密特正交化:得到标准正交向量组,即 大家既正交 又单位向量。
- 条件:
- 合同:P^{T}AP=B,则 A B 合同。
- 等价:r(A) = r(B),秩相等。如果 B 可由 A 经过一系列初等变换得到,则等价。
- 相似:P^{-1}AP=B,则 A B 相似。
二次型,正定矩阵,半正定矩阵。
- 二次型:
,
。
- 正定二次型:对任意一组不全为零的实数 x1..n,都有 f(x1..n) = X^{T}AX > 0。A 也称为正定矩阵。
- 正定矩阵的判定:(应该是充要了)特征值均为正(为零也不行)。
- 半正定:f ≥ 0,特征值均非负。负定 半负定 定义相似。
- 二次型:
Jordan 标准型:
- Jordan 块:

- Jordan 标准型:由 Jordan 块组成的 块对角矩阵。
- 化为 Jordan 标准型:任意方阵都可化为,初等因子法:
- 首先用初等变换,化特征矩阵 λE-A 化为对角形式,然后将主对角上的元素分解成 互不相同的一次因式方幂的乘积,则所有这些一次因式的方幂(相同的按出现的次数计算)就是 A 的全部初等因子。
- 然后就不会了。
- Jordan 块:
矩阵的微分,Hessian 矩阵,Jacobian 矩阵:
- 梯度,相当于多元标量函数 对向量求导。
- Hessian 矩阵,多元标量函数的二阶微分:
- Jacobian 矩阵,向量函数 对 向量微分,:
- 如果矩阵元素都是某个标量的函数,那么直接微分 大小和原矩阵一样。
- 矩阵乘法的微分:
什么是向量范数,矩阵范数?
- 范数定义:正定(零矩阵范数=0),齐次(|λA|=λ|A|),三角不等式(两边范数之和 ≥ 第三边范数)。
- 向量的 L1 norm,L2 norm,矩阵我没学过。
矩阵的幂运算:
- A^n = A^{n-1} · A = A · A^{n-1}。
- 相似对角化:如果 A = Q^{-1} · Λ · Q,那么直接对角阵元素 n 次方。
- 幂等矩阵:A^n = A,特征值只可能是 0 1,迹 = 秩 tr(A)=rank(A),A(E-A)=(E-A)A。
什么是 Pseudo Inverse 伪逆矩阵?
- (奇异矩阵 非方阵 不存在逆矩阵)逆矩阵的广义形式。
- 与 A 的转置矩阵 A' 同型的矩阵 X,并且满足:AXA=A, XAX=X
MATLAB解线性方程组的原理。
概率论
概率论和数理统计的区别与联系
- 概率论:更数学,从已知形式或某些参数的 分布 / 随机变量入手,推断出另一者的性质,比如 已知分布形式 求期望方差,已知随机变量参数 估计分布期望方差(大数定律 中心极限定理 这是数理统计的基础),已知事件间关系建模 求概率(全概率公式 贝叶斯公式)。
- 数理统计:更偏应用,基础是概率论,是概率论的应用,从实际出发,从采样出发,主要内容有参数估计、假设检验等。
- 知和用的关系。一个是发现规律,构造模型,证明定理。一个是选择模型,调整模型,应用模型。
什么是概率密度函数,性质:
- 连续型随机变量,f(x) 落在一段区间的概率 / 区间长度,取极限 区间长度 → 0。
- 总是 ≥ 0,∫f(x)dx = 1,P{X>x} = ∫_{-∞}^x f(x)dx
联合概率分布、条件概率分布、边缘概率分布:
- 条件概率:B 发生的情况下 A 发生的概率。
- 联合概率:包含多个条件的条件概率。
- 边缘概率:仅与单个随机变量有关的概率,剩下维度按分布求期望。
- 能否直接由边缘分布函数求得联合分布函数:两随机变量不相互独立 则不行。
大数定律(切比雪夫,伯努利,辛钦):
当样本数据无限大时,(形式 lim n→∞ P = 1)
- 样本均值 → 总体均值(切比雪夫,条件为方差有限大)
- 事件 A 发生的频率 → 概率(伯努利)
- 样本均值→ 数学期望(辛钦,条件为期望存在)
应用:多次采样平均减小误差。
中心极限定理:
- 当样本量 n 逐渐趋于无穷大时,n 个抽样样本的均值的频数,逐渐趋于正态分布 N(μ, σ²/n)。原总体的分布不做任何要求。
- 应用:1. 样本平均值 → 总体均值 / 期望,2. 样本方差 → 估计总体方差。
最大似然估计:
- 概率:结果没有产生之前,根据环境参数,预测某件事情发生的可能性;
- 似然:在确定的结果下,去推测产生这个结果的可能环境参数。
- L(θ|x) = P(x|θ)。既然已经观测到了这个现象,就取 让它出现概率最大 的环境参数值吧。
贝叶斯公式,应用:
- 已知 B 求 A 的概率,等于 AB 都发生概率 / B 发生的概率。
- 应用:通过发生的事情,反推环境是 xx 因素的概率。
全概率公式:
- 事件 A1,A2,…构成一个完备事件组(互斥且 Σ概率=1),那么 P(B) = Σ P(B|Ai) P(Ai)。
协方差 & 相关系数:
- 协方差:两随机变量 线性相关性的强度,\(Cov(X,Y)=E{[X−E(X)][Y−E(Y)]}\);
- 相关系数:归一化(不受变量尺度影响),Corr = 0 则不相关。 \(Corr(X,Y)=Cov(X,Y)/\sqrt{D(X)}\sqrt{D(Y)}\)。
- 协方差 / 相关系数 = 0 但仍然不独立:Y = X²。
正态分布 / 高斯分布:
- 若随机变量 X 服从一个数学期望为 μ、方差为 σ² 的正态分布,记为 N(μ, σ²)。
- 概率密度函数:
- 期望值 μ 决定了其位置,标准差 σ 决定分布的跨度。μ = 0, σ = 1:标准正态分布。
- 正态分布能积分出来吗:不太能,最多只有这个
- 应用场景:近似某些分布(中心极限定理),把成绩转换为正态分布(高考赋分)。
- 对正态分布,独立和不相关等价。
- (相互独立的)正态分布相加:μ1 + μ2,σ1² + σ2²。
- (相互独立的)正态分布相乘:(μ1σ2² + μ2σ1²) / (σ1² + σ2²),σ1²σ2² / (σ1² + σ2²)。
- (相互独立的)正态分布平方和:卡方分布。
- (相互独立的)正态分布联合: 多维正态分布,不相互独立 不一定。
指数分布 均匀分布 泊松分布 二项分布:公式
- 指数分布:
- \(f(x) = λe^{−λx}, x>0\)。X ~ Exp(λ)。
- 均匀分布:
- X ~ U(a, b): f(x) = 1/(b-a), a<x<b; 0, others。
- 泊松分布:
- 离散型随机变量,
,参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。
- 举例:医院平均每小时出生6个新生儿,想知道在起飞前一小时 是否有机会见到10个或更多的婴儿。预测这段时间来的客户数量。
- 离散型随机变量,
- 二项分布:离散型随机变量,n次独立重复的伯努利试验中,设每次试验中事件A发生的概率为p。n 次试验中事件 A 恰好发生 k 次,这个离散概率分布。 \(P\{X=k\}=C_n^kp^k(1-p)^{n-k}, C_n^k=\frac{n!}{k!(n-k)!}\)
- 指数分布:
参数估计:无偏性、有效性、相合性:
- 无偏性:参数估计的数学期望 \(E(\hat\theta)=\theta\) 。
- 有效性:(已经无偏)若对于任意 θ∈Θ,有 \(D(\hat\theta_1)\le D(\hat\theta_2)\)
- 相合性 / 一致性:在大样本条件下,估计值→真实值,n → ∞ 时 \(\hat\theta\) 依概率收敛于 θ,\(lim_{n\rarr\infin}P\{|\hat\theta-\theta|\le\epsilon\}=1\) 。
参数估计:点估计 & 区间估计:
- 区间估计:在推断总体参数时,还要估计出总体参数的一个区间,并同时给出总体参数落在这一区间的概率的保证。
- 点估计:常用方法有矩估计法、最大似然估计法。提供一个具体的数值估计,不能提供估计参数的估计误差大小。
参数估计:矩估计,最大似然估计,最小二乘法,贝叶斯估计。
矩估计:
- 矩:μl = E(X^l) = ∫ x^l * f(x|θ)。
- 令 想估计的矩 = 样本矩的平均值。
- 一阶样本原点矩 期望,二阶样本中心矩 方差。
最大似然估计:
- 将样本的联合概率密度函数看成
的函数,用 L(
,
) 表示,简记为 L(θ)。
- L(
) = L(
,
) = p(
;
) p(
;
)...p(
;
),取令 L(θ) 最大的 θ 值,可能会 乘法 → 加法 logL。
- 将样本的联合概率密度函数看成
贝叶斯学派:最大后验估计(结果里会多一堆超参数,这是先验在起作用)。
假设检验:
- 一般会提出一对 对立的假设,原假设 H0,备择假设 H1。
- 第一类错误 α:拒绝 H0 且 H0 为真,太激进;第二类错误 β:接收 H0 且 H0 为假,太保守。
- 保护原假设的原则:先限制犯第Ⅰ类错误的概率不超过 显著性水平 α,在此条件下,考虑如何使犯第 Ⅱ 类错误的概率 β 尽可能小。
- 正态分布的应用:假设分布为正态分布,方便做假设检验。
- 双边检验(温度不能过高也不能过低) & 单边检验(只要不往牛奶里掺水就 ok,牛奶当然越浓越好)。
- p 值检验:计算检验统计量,根据最小显著性水平 p,决定接收 / 拒绝 H0。
机器学习
梯度 & 梯度下降,为什么梯度下降?
- 梯度:多元标量函数想象成山峦,最陡的方向。
- 梯度下降:通用的找局部最优的方法,很多问题性质不够好,没法数学公式一步求得可接受的解,因此为到达最低点,沿最陡下降方向 一步一步走。
距离度量方式:【】
- 马氏距离:
- 曼哈顿距离:
- 欧式距离:
- 余弦距离:
- 相关系数:
MSE 为什么是 Σ(yi-y)² 而不是立方?
- 欧几里得距离具有旋转不变性,即不管坐标轴怎么转,某点到原点的距离都不变。L3 norm 没有。
最小二乘法。
最小二乘法是解决曲线拟合问题最常用的方法。其基本思路是:令
其中,
是事先选定的一组线性无关的函数,
是待定系数
,拟合准则是使
与
的距离
的平方和最小,称为最小二乘准则。
什么是 SVD 分解。
- 主对角线上每个元素都称为奇异值 singular value。U V 都是酉矩阵(转置矩阵 = 逆矩阵)。

- 应用:
- PCA:对数据的协方差矩阵进行 SVD 分解
,根据特征值大小,取前 r 列特征向量 和 特征值,用列特征向量进行降维
。
- 推荐系统:
- 对比用户的相似性,将用户A喜欢的手机品牌 推送给 与A相似 但是手机品牌喜好未知的 用户B。
- 用户-商品打分矩阵M(即行代表不同的商品,列代表不同的用户,
代表第 i 个用户对第 j 个商品的喜欢程度)分解成
。其中 U 代表了用户的特征矩阵,V 代表了商品的特征矩阵,为了降低噪声影响会只取前 r 列。
- 当一个新用户数据进来
(对某些商品的喜好程度未知,未知的列设为0)后,会与 对角矩阵 商品特征矩阵 相乘,得到它的用户特征:
, 然后将这个新的用户特征 u 与老用户特征矩阵 U 每一行比对(比如用欧式距离),距离最近的那一行 即是最相似的老用户。
- PCA:对数据的协方差矩阵进行 SVD 分解
- 主对角线上每个元素都称为奇异值 singular value。U V 都是酉矩阵(转置矩阵 = 逆矩阵)。
什么是 LDA,和 SVM 的联系与区别?
线性判别分析 LDA:
- 监督学习的降维技术,数据集的每个样本带有类别信息,这点和 PCA 不同,PCA 是不考虑样本类别输出的无监督降维技术。
- 思想:投影后类内方差最小,类间方差最大。我们要把数据往低维度上投影,希望每一种类别数据 的 投影点 尽可能接近,而不同类别数据 的 类别中心之间,距离尽可能大。一般使用 SVD 分解。
- LDA 不适合对非高斯分布样本进行降维,PCA 也有这个问题。
支持向量机 SVM:
- 二分类技术,分类超平面跟两类数据的间隔要尽可能大(即远离两边数据)
- 先将数据变成线性可分的,再构造出最优分类超平面;通过选择一个核函数 K ,将低维非线性数据映射到高维空间中。
或许可以让 LDA 当作 SVM 的核函数?不过听说 SVM 也不怕高维度呀,难道是怕过拟合吗?
什么是 Normal Equation 正规方程 标准方程?
- https://blog.csdn.net/jingyi130705008/article/details/78866757
- 线性回归中,为了求得 cost function 最小的参数值θ,我们一般采用梯度下降法,但是当训练样本较小时(不超过千数量级),采用 Normal Equation 进行求解更好。(不能用于不可逆矩阵)
GMM 高斯混合模型:
- 聚类算法,用于表示可聚类为多个高斯分布的任何数据集。
- GMM 由两部分组成:均值向量 (μ) 和协方差矩阵 (Σ)。
卷积网络:
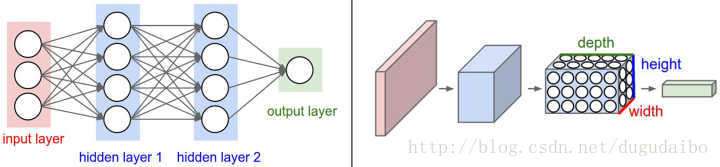
- 输入层、卷积层,ReLU层、池化(Pooling)层、全连接层。
循环神经网络 RNN,LSTM,TCN:
- RNN:
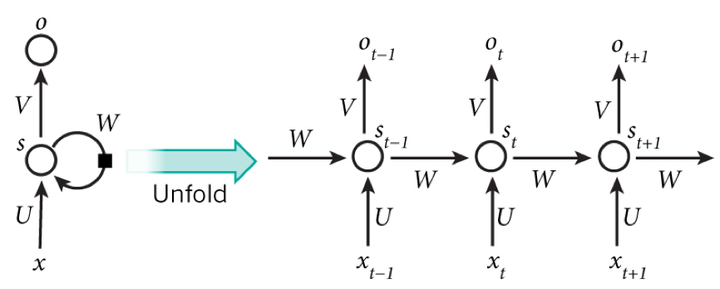
- LSTM:RNN 的问题:不适用于长期记忆。基本思想:
- 引入“门运算”,遗忘门 输入门,选择性记忆。
- 引入“门运算”,将梯度中的累乘变为累加,解决梯度消失问题
- TCN:RNN 的问题:只能串行计算,要保存所有中间变量,因此非常计算密集。因果卷积 && 空洞 dilated 卷积 + 残差模块。
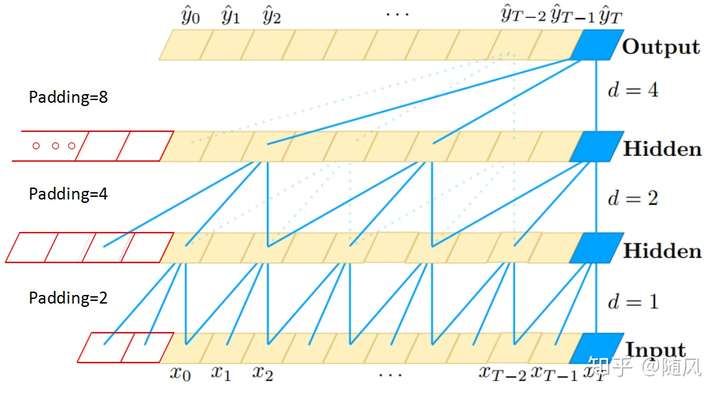
- RNN:
复变函数
复变函数求导:
- 极限 lim {Δz→0} [f(z0+Δz) - f(z0)] / Δz 存在,则可导,lim = 导数。
- Δz 的方向是任意的,任意方向都要存在。
解析,解析函数,奇点:
- 函数在某点解析:如果在 z0 及 z0 的邻域里处处可导,则在 z0 解析。
- 解析函数:如果在区域 D 上处处解析,则是解析函数。
- 某点解析 => 某点可导,区域解析 <=> 区域可导。
- 奇点:f 在 z0 不解析。广义上奇点指未定义的点(如除零)
- 孤立奇点:但 z0 的任意邻域里总有 f 的解析点。
- 性质:单连通域内 环路积分 = 0,复连通域内 广义环路积分(即包括内外边界,内边界取顺时针为正)= 0,导函数仍然是解析函数。
Cauchy-Riemann 条件:
- 某点可导充要条件:f = u + iv,该点 u v 可微,且偏导数满足 C-R 方程(ux = vy, uy = -vx)。导数 f' = ux + ivx = vy - iuy
- 区域解析充要条件:区域内 u v 可微,且偏导数满足 C-R 方程(ux = vy, uy = -vx)。
复变函数积分:
- 柯西积分定理 / 积分基本定理:解析函数积分与路径无关,环路积分 = 0。
- 柯西积分公式:
- 高阶导数公式(柯西积分公式 两边对 z0 求导):
Abel 定理:
- 绝对收敛:
收敛,可由 实部虚部级数 |a| |b| 绝对收敛推出。
- (收敛但不绝对收敛:Σ 1/n)
- 幂级数在 x0 处收敛,则半径<x0 都绝对收敛;在 x1 出发散,则半径>x1 都发散。
- 绝对收敛:
洛朗级数 Laurent:
- 对于一片收敛的区域,可以直接 taylor 级数:
,
。
- 洛朗级数:解析环域:k 也可以 -1 ~ -n。
- 解析部分:n ≥ 0;主要部分:n<0。无穷远处逆号。
- 对于一片收敛的区域,可以直接 taylor 级数:
留数:
- 留数定理:环路积分 = 环路围的那几个奇点 绕一周积分 = 2Πi Σ 奇点留数。
- 留数:孤立奇点 z0 处 laurent 展开,
- 无穷远点的留数:如果 |z| > R 都解析,则无穷远点是孤立奇点,
- 求无穷远留数 不想积分:
- 扩展留数定理,所有奇点的留数之和为零(包括无穷远)。
奇点分类:
- 可去奇点:比如 sin z / z,只要定义得当就完全解析,Res = 0
- 极点:负幂项有限(不会高过 -m 次),
在某个点
是孤立奇点,但是
在
可能就变成了可去奇点。
。
- 本性奇点:负幂项无穷多。
其他
数学相关课程中,最有难度的一个知识点是什么。
- 积分不费解,因为物理竞赛。矩阵乘法 → 秩 → 特征值特征向量 费解。
高斯白噪声:
- gaussian:幅度 / 瞬时值 分布服从高斯分布。
- white:它的二阶矩不相关,一阶矩为常数,功率谱密度(在较宽的频率范围内)服从均匀分布,是指先后信号在时间上的相关性。
- 分析信道加性噪声的理想模型,热噪声(通信中的主要噪声源)属于高斯白噪声。
Markov 性,Markov 过程:
- 给定现在状态 及所有过去状态,其未来状态的条件概率分布 仅依赖于当前状态,与过去状态(即该过程的历史路径)是条件独立的。
- Markov 过程:具有 Markov 性质的过程。
- 时间 状态 都是离散的马尔可夫过程称为马尔可夫链。
什么是 Convex:
- 凸函数:一元:

- 函数值的平均 ≥ 平均值的函数 下凸。多元函数定义类似。凸优化问题,局部最优解是全局最优解。
- 判定:二阶导数 ≥ 0,多元函数 如果 Hessian 矩阵 半正定矩阵,则凸函数。
- 凸函数:一元:
什么是李雅普诺夫稳定性(自控,不太会)。
什么是丰度(不知道)。
投影算子的概念(实变函数,不太会)。
cs 保研经验贴 | 数学试题 · 自动化所特供版的更多相关文章
- cs 保研经验贴 | 综合面试题库
绝大部分夏令营都需要面试:如果幸运的话,稍微问几个问题就结束了:不幸的话,可能要抓住你做项目.读论文.复现.做 pre 等等. 这篇博客适用于幸运的情况:绝大部分学校的面试题库,都是彼此重合的,并且一 ...
- 保研经验帖----江西师范大学 to 华中科技大学
呼,距离拿到华科cs的offer也有一段时间,有好几次准备动手写这篇经验帖,但就是理不清自己想表达什么,今早起来状态还不错,洗漱的时候思路居然通透了,哈哈哈~ 一.基本情况 先简单介绍笔者的一些基本情 ...
- SAP成都研究院Sunshine: 我的C4C实习感受和保研之路
今天的文章来自SAP成都一位实习生,曾经和Jerry同在C4C成都开发团队一起工作过.在Sunshine最后一个工作日里,Jerry和Sunshine一起吃饭的时候,她曾经聊到接下来的保研打算和将来工 ...
- 计算机保研,maybe this is all you need(普通双非学子上岸浙大工程师数据科学项目)
写在前面 9.28接收了拟录取通知,也终究是尘埃落定了,我人生的又一个阶段也终于结束.面对最终录取结果,或多或少会有所遗憾,但也还是基本达到了预期的目标了. 作为在今年严峻的保研形势下幸存的我,一直想 ...
- 我的美国(北美)计算机CS实习面试经验分享
过去的一年多里,参加了一些面试,虽然面过的公司不多,但都从头一直走到尾.毕竟自己也是花了大量的时间和精力在这一场场的面试里.所以,就絮叨下自己的一些经验,希望能给在美国找实习找工作的同学们提供一点点帮 ...
- 一年java工作经验的面试题总结(持续更新中)
本人是17年6月份毕业的,3月份出来实习,算起来也是工作一年了吧,金三银四,博主也考虑换一份工作,于是最近面试了几家,总结一下面试中的问题,大家一起交流学习. 第一次面试 ①说下java类的加载 ② ...
- 保研机试训练[bailianoj]
site:http://bailian.openjudge.cn/xly2018/ 1.计算任意两天之间的天数 思路:以0为起始点计算天数,然后相减即可.这样的编码复杂度会减少很多. #include ...
- 题目1205:N阶楼梯上楼问题(2008年华中科技大学计算机保研机试真题:递推求解)
题目1205:N阶楼梯上楼问题 时间限制:1 秒 内存限制:128 兆 特殊判题:否 提交:2447 解决:927 题目描写叙述: N阶楼梯上楼问题:一次能够走两阶或一阶,问有多少种上楼方式. (要求 ...
- 我的CS考研路
说在前面 从去年7月15号正式准备考研以来,直到今天,3月19号,一共经历8个多月,考研初步告捷,在此想跟大家分享一下自己的经验,希望能对接下来考研的学弟学妹们有所帮助. 首先介绍下我自己的情况,本科 ...
- 关于如何学好游戏3D引擎编程的一些经验[转]
此篇文章献给那些为了游戏编程不怕困难的热血青年,它的神秘要我永远不间断的去挑战自我,超越自我,这样才能攀登到游戏技术的最高峰 ——阿哲VS自己 QQ79134054多希望大家一起交流与沟通 这篇文章是 ...
随机推荐
- 安卓之各组件的LayoutParams分析
文章摘要 在Android开发中,LayoutParams是一个非常重要的概念,它用于描述View在其父容器中的布局行为.不同的ViewGroup有不同的LayoutParams子类,例如Linear ...
- 介绍一款轻量型 Web SCADA 组态软件
随着互联网.物联网技术的快速发展,图扑物联基于多年研发积累和私有部署实践打磨.以及对业务场景的深入理解,推出了适用于物联网应用场景的轻量型云组态软件. 该产品采用 B/S 架构,提供 Web 管理 ...
- 【UniApp】-uni-app-自定义组件
前言 经过上个章节的介绍,大家可以了解到 uni-app-网络请求的基本使用方法 那本章节来给大家介绍一下 uni-app-自定义组件 的基本使用方法 原本打算是直接写项目的,在写项目之前还有个内容需 ...
- Python——第四章:函数的递归调用
递归: 函数自己调用自己 递归如果没有任何东西拦截的话. 它默认就是一个死循环 def func() func() func() 因此递归调用的时候需要有判断,来退出循环 def func() if ...
- Lean大神编译的OpenWRT问题汇总
1.初始密码为password,登录路由器后第一件事要修改默认密码 2.Lean大神编译的OpenWRT无法SSH.SFTP, 3.为了方便操作,一定要编译的时候安装TTYD,但是TTYD默认无法打开 ...
- MySQL|MySQL执行计划
使用explain关键字可以模拟优化器执行SQL查询语句,从而知道MySQL是如何处理你的SQL语句的,分析你的查询语句或是表结构的性能瓶颈. explain执行计划包含的信息 每列的内容 列 含义 ...
- MySQL|MySQL事物以及隔离级别
MySQL 事务主要用于处理操作量大,复杂度高的数据.比如开单,需要添加给订单表增加记录,还需要增加订单的各种相关明细,操作复杂度高,这些操作语句需要构成一个事务.在 MySQL 命令行的默认设置下, ...
- Spring Boot与Shiro和Mybatis整合
1:shiro是什么? Apache Shiro 是ASF旗下的一款开源软件 shrio是一款强大而灵活的安全框架 可为任何应用提供安全保障- 从命令行应用.移动应用到大型网络及企业应用 2:shir ...
- vue2升级vue3:webpack vue-loader 打包配置
如果没有啥特别的需求还是推荐vue-cli! vite vue3 TSX项目 虽然vite 很香,但是vite rollup 动态加载,多页面 等问题比较难搞 vite的缺点 wepback _ ...
- LAS Spark 在 TPC-DS 的优化揭秘
更多技术交流.求职机会,欢迎关注字节跳动数据平台微信公众号,回复[1]进入官方交流群 文章主要介绍了火山引擎湖仓一体分析服务 LAS Spark(下文以 LAS Spark 指代)在 TPC-DS 上 ...