对比python学julia（第二章）--（第二节）勾股树

2.1.问题描述

　　二话不说，先上图：

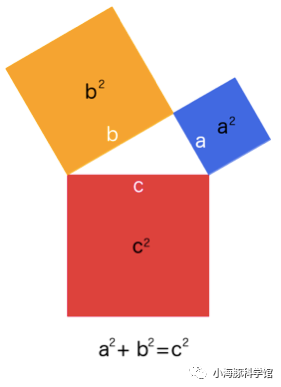
图一、勾股定理图形图二、勾股树

　　怎么样？是不是很漂亮？勾股树是根据勾股定理绘制的可以无限重复的图形，重复多次之后呈现为树状。据说勾股树最早是由古希腊数学家毕达哥拉斯绘制，因此又称之为毕达哥拉斯树。这种图形在数学上称为分形图，它们中的一个部分与其整体或者其他部分都十分相似，分形体内任何一个相对独立的部分，在一定程度上都是整体的再现和缩影。这就是分形图的自相似特性。

　　我国古代把直角三角形称为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以把这个定理称为勾股定理。

　　公元前 6 世纪，古希腊数学家毕达哥拉斯证明了勾股定理，因而西方人都习惯地称这个定理为毕达哥拉斯定理。

　　勾股定理的定义：在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。

　　用数学语言表达为a²+b²=c²，用图形表达如上图一所示。

　　以图一中的勾股定理图为基础，让两个较小的正方形按勾股定理继续“生长”，又能画出新一代的勾股定理图，如此一直画下去，最终得到一棵完全由勾股定理图组成的树状图形(见图二) ，称其为勾股树再恰当不过。

　　下面我们用Python和Julia分别绘制勾股树分形图

2.2.算法分析

　　利用分形图的自相似特性，先构造出分形图的基本图形，再不断地对基本图形进行复制，就能绘制出分形图。针对勾股树分形图，其绘制步如下：

　　(1) 先画出图一所示的勾股定理图形作为基本图形，将这一过程封装为一个绘图函数，以便迸行递归调用。

　　(2) 在绘两个小正方形之前，分别以直角三角形两条直角边作为下一代勾股定理图形中直角三角形的斜边以递归方式调用绘图函数画出下一代的基本图形。

　　(3) 重复执行前两步，最终可绘出一棵勾股树的分形图。由于是递归调用，需要递归的终止条件，这里设置为某一代勾股定理图的直角三角形的斜边小于某个数值时就结束递归调用。

　　如图三所示，这是一棵经典勾股树分形图的绘制过程，可以看到它从一个勾股定理图开始，逐步成长为一棵茂盛的勾股树。

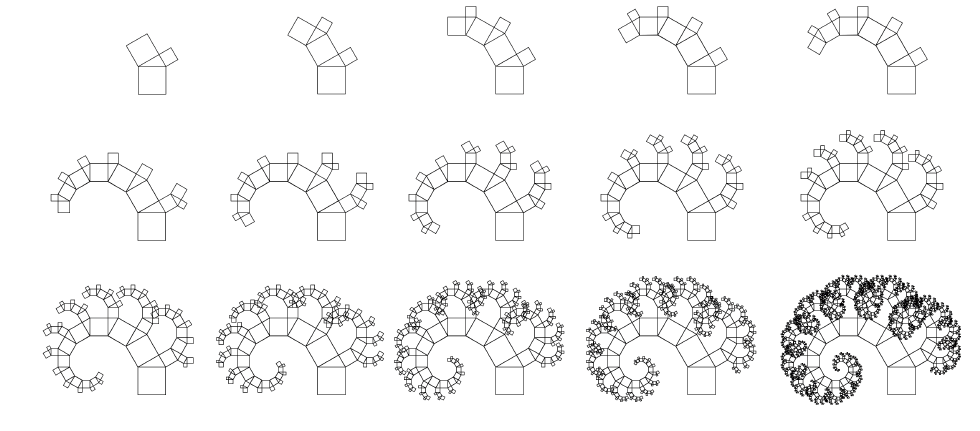
图三经典勾股树绘制过

2.3.编程解题

　　Python语言内置了一个绘图模块”海龟绘图（Turtle Graphics）”,非常适合绘制勾股树。

　　海归绘图模块是早期的 LOGO 编程语言在 Python 语言中的实现。使用这个模块绘图时，可以把屏幕当成一块画布，通过控制一个小三角形(或小海龟)的画笔在画布上移动从而在它前进的路径上绘制出图形。这和 Scratch 中画笔的功能类似。

　　海归绘图（turtle）模块提供一套用于绘图的函数，在使用之前要先导人 turtle 模块。

　　打开 IDLE环境，在 Python Shell 窗口中使用 import 语句导人 turtle 模块：

　　>>> import turtle

　　输人下面一行代码:

　　>>> turtle.fd(100)

　　这时会出现一个标题为 Python Turtle Graphics 的窗口，在窗口中央有一个小三角形图标向右移动并画出一条直线，如图四所示。

　　如果看不到这个窗口，可能是被 Python Shell 窗口遮挡住了。

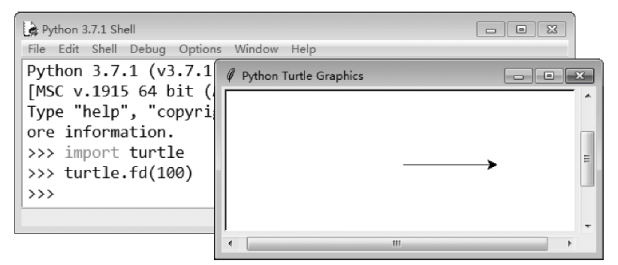
图四

　　如果不想每次都用turtle.fd(100)这种方式，可以用下面的方式，就简洁很多：

　　>>> from turtle import *

　　>>> fd(100)

　　关于海龟绘图模块的画布坐标系统、画笔运动控制、画笔设置等，可以参考原书或网上查询相关资料，这里不再赘述。

让我们来看看最终的Pyton代码：

 1 '''

 2 程序：绘制勾股树

 3 作者：苏秦@小海豚科学馆公众号

 4 来源：图书《Python趣味编程：从入门到人工智能》

 5 '''

 6 from turtle import *

 7 from math import cos, radians

 8

 9 def square(b):

10     '''画正方形'''

11     for i in range(4):

12         fd(b)

13         right(90)

14

15 def draw(b):

16     '''画勾股树'''

17     if b < 50: return

18

19     square(b)

20

21     fd(b)

22     left(30)

23     draw(b * cos(radians(30)))

24     square(b * cos(radians(30)))

25

26     right(90)

27     fd(b * cos(radians(30)))

28     draw(b * cos(radians(60)))

29     square(b * cos(radians(60)))

30

31     right(90)

32     fd(b * cos(radians(60)))

33     right(30)

34     fd(b)

35     right(90)

36     fd(b)

37     right(90)

38

39 if __name__ == '__main__':

40     speed(0)

41     up()

42     goto(50, -250)

43     down()

44     seth(90)

45     draw(100)

　　不幸的是，julia语言没有内置类似海龟绘图的模块，不过好在已经有人提供了第三方库实现类似海龟绘图的功能。这个第三方库就是Luxor，并且是开源的，开源地址在这里：https://github.com/JuliaGraphics/Luxor.jl。

　　Luxor是绘制简单静态矢量图形的Julia包，它提供了用于处理形状、多边形、剪切蒙版、PNG和SVG图像、海龟图形和简单动画的基本绘图功能和实用工具。以上是Julia开发文档中的介绍原话（当然，原话是英文的），笔者觉得已经非常清晰全面，就原文照搬过来了。

　　首先用我们之前介绍的方法安装Luxor包，当然最简单的方法就是在REPL环境下输入：using Luxor,如果没有安装Luxor包，编程环境会提示你没有安装该包，是否要安装，输入y，接下来跟着提示操作，就能顺利安装Luxor包。

　　然后我们来看一个例子：

1 using Luxor

2 Drawing(500, 500, "my-drawing.svg")

3 origin()

4 setcolor("red")

5 circle(Point(0, 0), 100, :fill)

6 finish()

7 preview()

　　这段简短的代码完成以下工作：

绘制一个500单位的正方形（通常我们称之为画布），并以SVG格式保存在“my-drawing.svg”中。
将零点从左上角移动到中心。图形引擎通常从左上角开始测量(偶尔从左下角开始)，但如果从中心开始，则更容易计算出物体的位置。
origin()函数将0/0点(坐标原点)移动到图形的中心。
选择200种左右颜色中的一个(在colors .jl中定义)。
以x = 0, y = 0为圆心绘制一个半径为100个单位的圆，并用当前的颜色填充它。
完成绘制并在屏幕上显示它。（笔者注：Luxor没有图形界面，它通常打开操作系统默认浏览器显示svg文件，默认图像软件显示PNG图片等，并且该功能只在REPL环境下有效）。

　　关于Luxor更多的绘图知识，不在本文的讨论范围内。这里重点介绍在Luxor中包含的海龟绘图模块。

　　Luxor提供了一些基本的“海龟图形”功能。控制海龟:向前、转弯、圆形、方向、朝向、矩形、向下、向上、笔画颜色、笔画宽度和重新定位，等等，并且角度以度而不是弧度为单位（这一点与Python的海龟绘图模块不同）。

　　定义一个海龟对象是这样的：turtle=Turtle().而下面的代码将绘制一条直线：

using Luxor

turtle=Turtle()

Forward(turtle,100)

finish()

　　以下是海龟绘图模块的动作函数：

海龟绘图函数	对应动作
Forward	More forward by d units
Turn	Increase the turtle's rotation by n degrees
Circle	Draw filled circle centered at current pos
HueShift	Shift the Hue of the turtle's pen color by n
Message	Output text
Orientation	Set the turtle's orientation to n degrees
Pen_opacity_random	Set opacity to random value
Pencolor	Set the Red, Green, and Blue values
Pendown	Start drawing
Penup	Stop drawing
Penwidth	Set the width of the line to n
Pop	Move turtle to the value stored on the stack
Push	Save the turtle's position on the stack
Randomize_saturation	Randomize the saturation of the current color
Rectangle	Draw filled rectangle centered at current pos
Reposition	Place turtle at new position
Towards	Rotate turtle to face towards a point

　　具体函数的参数大家可以到这个网址查阅：http://juliagraphics.github.io/Luxor.jl/dev/howto/turtle/

　　据此我们可以用Luxor的海龟绘图模块来绘制勾股树了。打开VSCode，新建ggs.li,输入代码如下：

 1 =#

 2 using Luxor

 3

 4 function square(turtle::Turtle,b)

 5     #画正方形

 6     for i in 1:4

 7         Forward(turtle,b)

 8         Turn(turtle,-90)

 9     end

10 end

11

12 function draw(turtle::Turtle,b)

13     #画勾股树'''

14     if b < 5

15         return

16     end

17     square(turtle,b)

18

19     Forward(turtle,b)

20     Turn(turtle,30)

21     draw(turtle,b * cosd(30))

22     square(turtle,b * cosd(30))

23

24     Turn(turtle,-90)

25     Forward(turtle,b * cosd(30))

26     draw(turtle,b * cosd(60))

27     square(turtle,b * cosd(60))

28

29     Turn(turtle,-90)

30     Forward(turtle,b * cosd(60))

31     Turn(turtle,-30)

32     Forward(turtle,b)

33     Turn(turtle,-90)

34     Forward(turtle,b)

35     Turn(turtle,-90)

36 end

37

38 function main()

39     Drawing(1000, 800, "ggs.svg")

40     origin()

41     turtle=Turtle()

42     #@svg begin

43         draw(turtle,100)

44     #end

45     finish()

46 end

47 main()

　　这段代码会在代码文件同目录下生成ggs.svg文件，并绘制一幅勾股树图形。

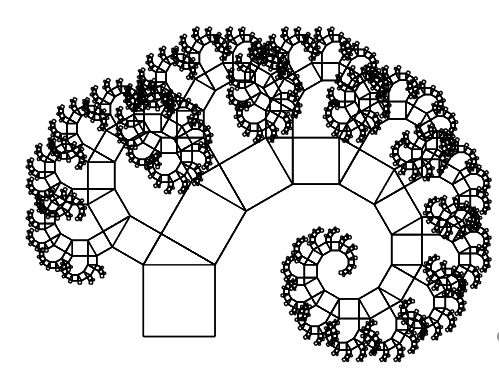
　　对比Python代码，我们可以发现它们之间没有多大差别。有一点要注意，Python的三角函数的参数是弧度，所以要用radians函数将度转换为弧度(如：cos(radians(30)))，而julia分cos（）、cosd()两类函数，前者的参数是单位是弧度，后者的参数单位是度。