深度优先搜索DFS(一)
/**
* Copyright(c)
* All rights reserved.
* Author : Mered1th
* Date : 2019-02-20-13.12.15
* Description : Bag
*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<unordered_set>
#include<map>
#include<vector>
#include<set>
using namespace std; const int maxn=30;
int n,V,maxValue=0;//物品件数,背包容量,最大价值
int w[maxn],c[maxn]; //每件物品的重量,每件物品的价值
void DFS(int index,int sumW,int sumC){
if(index==n){
if(sumW<=V&&sumC>maxValue){
maxValue=sumC;
}
return;
}
DFS(index+1,sumW,sumC); //不选
DFS(index+1,sumW+w[index],sumC+c[index]); //选
} int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif
scanf("%d%d",&n,&V);
for(int i=0;i<n;i++){
scanf("%d",&w[i]);
}
for(int i=0;i<n;i++){
scanf("%d",&c[i]);
}
DFS(0,0,0);
printf("%d\n",maxValue);
return 0;
}
5 8
3 5 1 2 2
4 5 2 1 3
输出:
10
void DFS2(int index,int sumW,int sumC){
if(index==n){
return;
}
DFS2(index+1,sumW,sumC);
if(sumW+w[index]<=V){ //放的进去则选index件物品
if(sumC+c[index]>maxValue){
maxValue=sumC+c[index];
}
DFS2(index+1,sumW+w[index],sumC+c[index]);
}
}
bool in[maxn]={0};
void DFS3(int index,int sumW,int sumC){
if(index==n||sumW>=V){
if(sumC>maxValue){
maxValue=sumC;
}
return;
}
int i=index;
for(;i<n;i++){
if(w[i]+sumW<=V && in[i]==false){ //如果能放进去,且该物品不在背包里面
sumW+=w[i];
sumC+=c[i];
in[i]=true;
DFS3(index+1,sumW,sumC);
sumW-=w[i]; //回溯
sumC-=c[i];
in[i]=false;
}
}
}
vector<int> ans;
map<int,vector<int> > temp;
void DFS4(int index,int sumW,int sumC){
if(index==n||sumW>=V){
if(sumC>maxValue){
maxValue=sumC;
temp[maxValue]=ans;
}
return;
}
int i=index;
for(;i<n;i++){
if(w[i]+sumW<=V&&in[i]==false){
sumW+=w[i];
sumC+=c[i];
in[i]=true;
ans.push_back(i);
DFS4(index+1,sumW,sumC);
ans.pop_back();
sumW-=w[i];
sumC-=c[i];
in[i]=false;
}
}
} int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif
scanf("%d%d",&n,&V);
for(int i=0;i<n;i++){
scanf("%d",&w[i]);
}
for(int i=0;i<n;i++){
scanf("%d",&c[i]);
}
DFS4(0,0,0);
printf("%d\n",maxValue);
for(int i=0;i<temp[maxValue].size();i++){
cout<<temp[maxValue][i]<<" ";
}
return 0;
}
问题:给定一个序列,枚举这个序列的所有子序列(可以不连续),例如对序列{1,2,3}来说,它的所有子序列为{1}、{2}、{3}、{1,2},{1,3}、{2,3}、{1,2,3}。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<unordered_set>
#include<map>
#include<vector>
#include<set>
using namespace std;
vector<int> ans;
void dfs(string str,int index,string res){
if(index==str.length()){
if(res.size()==0) return; //否则会把“”也输出
int temp=stoi(res);
ans.push_back(temp);
return;
}
dfs(str,index+1,res); //选index
dfs(str,index+1,res+str[index]);//不选index
}
int main(){
string a="123";
dfs(a,0,"");
sort(ans.begin(),ans.end()); //排序
for(auto it=ans.begin();it!=ans.end();it++){
cout<<*it<<endl;
}
return 0;
}
变式:给定N个整数(可能有负数),从中选择K个数,使得这K个数之和恰好等于一个给定的整数X;如果有多种方案,选择他们中元素平方和最大的一个。
const int maxn=110;
int n,k,x,maxsumSqu=-1,A[maxn];
vector<int> temp,ans;
void DFS(int index,int nowK,int sum,int sumSqu){
if(nowK==k && sum==x){
if(sumSqu>maxsumSqu){
maxsumSqu=sumSqu;
ans=temp;
}
return;
}
if(index==n || nowK>k || sum>x){
return;
}
temp.push_back(A[index]);
DFS(index+1,nowK+1,sum+A[index],sumSqu+A[index]*A[index]);
temp.pop_back();
DFS(index+1,nowK,sum,sumSqu);
}
实例三 全排列问题:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<unordered_set>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=10;
bool isUsed[maxn]={0};
vector<int> num;
int n;
void dfs(int index){
if(index==n){
for(int i=0;i<num.size();i++){
printf("%d",num[i]);
}
printf("\n");
return;
}
for(int i=1;i<=n;i++){
if(isUsed[i]==true) continue;
num.push_back(i);
isUsed[i]=true;
dfs(index+1);
num.pop_back();
isUsed[i]=false;
}
} int main(){
n=3;
dfs(0);
return 0;
}
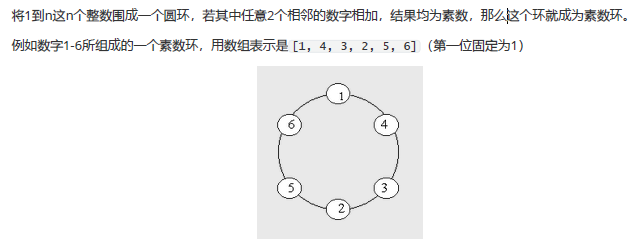
实例四 素数环问题(含剪枝):
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<unordered_set>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=100;
bool isPrime[maxn]; //假设都为质数
vector<int> ans;
bool isUsed[maxn];
int n; void getPrimeTable(){
memset(isPrime,1,sizeof(isPrime));
isPrime[0]=isPrime[1]=false;
for(int i=2;i<maxn;i++){
if(isPrime[i]){
for(int j=i+i;j<maxn;j=j+i){
isPrime[j]=false;
}
}
}
} void dfs(int index){
if(index>=n){
int temp=ans[0]+ans[index-1]; //判断第一个数和最后一个数之和
if(isPrime[temp]==false){
return;
}
for(int x:ans){
printf("%d ",x);
}
printf("\n");
return;
}
for(int i=2;i<=n;i++){
if(isUsed[i]==true) continue;
int temp=ans[index-1]+i;
if(isPrime[temp]==false) continue; //剪枝
ans.push_back(i);
isUsed[i]=true;
dfs(index+1);
ans.pop_back();
isUsed[i]=false;
}
} int main(){
getPrimeTable();
n=4;
ans.push_back(1);
dfs(1);
return 0;
}
6 7
0 1 1 1 0 0 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 1 1 1 0
1 1 1 0 1 0 0
1 1 1 1 0 0 0
4
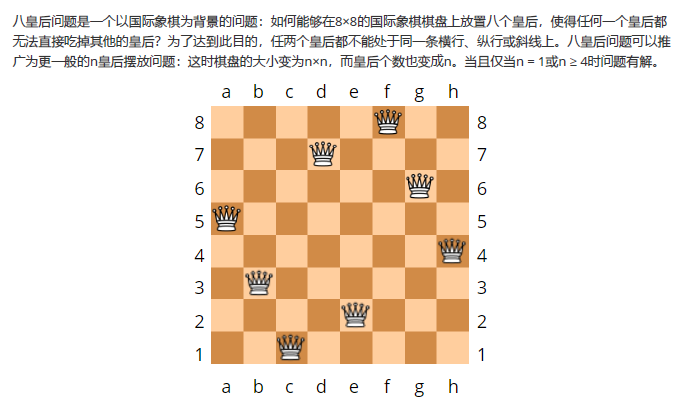
 求如图所示“块”的个数
求如图所示“块”的个数
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<unordered_set>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=100;
int X[4]={0,0,1,-1};
int Y[4]={1,-1,0,0};
struct node{
int x,y;
}Node;
int n,m; //¾ØÕó´óСΪn*m
int matrix[maxn][maxn];
bool inq[maxn][maxn]; bool judge(int x,int y){
if(x>=n||x<0||y>=m||y<0) return false;
if(matrix[x][y]==0||inq[x][y]==true) return false;
return true;
} void DFS(int u,int v){
inq[u][v]=true;
for(int i=0;i<4;i++){
int newX=u+X[i];
int newY=v+Y[i];
if(judge(newX,newY)){
inq[newX][newY]=true;
DFS(newX,newY);
}
}
}
int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif
scanf("%d%d",&n,&m);
for(int x=0;x<n;x++){
for(int y=0;y<m;y++){
scanf("%d",&matrix[x][y]);
}
}
int ans=0;
for(int x=0;x<n;x++){
for(int y=0;y<m;y++){
if(matrix[x][y]==1&&inq[x][y]==false){
ans++;
DFS(x,y);
}
}
}
printf("%d\n",ans);
return 0;
}
这里用到一个技巧就是:
int X[4]={0,0,1,-1};
int Y[4]={1,-1,0,0};
for(int i=0;i<4;i++){
int newX=u+X[i];
int newY=v+Y[i];
}
当矩阵过大时,DFS效率远不如BFS,下面给出BFS解法:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<unordered_set>
#include<map>
#include<vector>
#include<set>
#include<queue>
using namespace std;
const int maxn=100;
int X[4]={0,0,1,-1};
int Y[4]={1,-1,0,0};
struct node{
int x,y;
}Node;
int n,m;
int matrix[maxn][maxn];
bool inq[maxn][maxn]; bool judge(int x,int y){
if(x>=n||x<0||y>=m||y<0) return false;
if(matrix[x][y]==0||inq[x][y]==true) return false;
return true;
} void BFS(int x,int y){
queue<node> Q;
Node.x=x;
Node.y=y;
Q.push(Node);
inq[x][y]=true;
while(!Q.empty()){
node top=Q.front();
Q.pop();
for(int i=0;i<4;i++){
int newX=top.x+X[i];
int newY=top.y+Y[i];
if(judge(newX,newY)){
Node.x=newX,Node.y=newY;
Q.push(Node);
inq[newX][newY]=true;
}
}
}
} int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif
scanf("%d%d",&n,&m);
for(int x=0;x<n;x++){
for(int y=0;y<m;y++){
scanf("%d",&matrix[x][y]);
}
}
int ans=0;
for(int x=0;x<n;x++){
for(int y=0;y<m;y++){
if(matrix[x][y]==1&&inq[x][y]==false){
ans++;
BFS(x,y);
}
}
}
printf("%d\n",ans);
return 0;
}

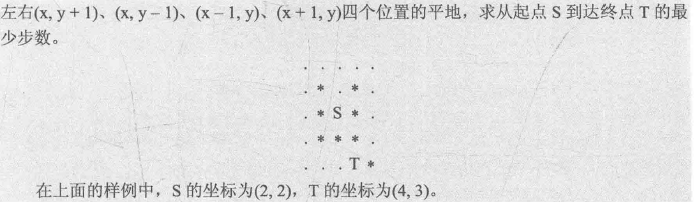
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<unordered_set>
#include<map>
#include<vector>
#include<set>
#include<queue>
using namespace std;
const int maxn=100;
struct node{
int x,y;
int step;
}S,T,Node;
int n,m;
char matrix[maxn][maxn];
bool inq[maxn][maxn]={false};
int X[4]={0,0,1,-1};
int Y[4]={0,0,1,-1}; bool judge(int x,int y){
if(x>=n||x<0||y>=m||y<0) return false;
if(matrix[x][y]=='*') return false;
if(inq[x][y]==false) return false;
return true;
} int BFS(){
queue<node> q;
q.push(S);
while(!q.empty()){
node top=q.front();
q.pop();
if(top.x==T.x&&top.y==T.y) return top.step; //到达终点,直接返回当前步数
for(int i=0;i<4;i++){
int newX=top.x+X[i];
int newY=top.y+Y[i];
if(judge(newX,newY)){
Node.x=newX,Node.y=newY;
Node.step=top.step+1;
q.push(Node);
inq[newX][newY]=true;
}
}
}
return -1;
} int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++){
getchar();
for(int j=0;j<m;j++){
matrix[i][j]=getchar();
}
matrix[i][m+1]='\0';
}
scanf("%d%d%d%d",&S.x,&S.y,&T.x,&T.y);
S.step=0;
printf("%d\n",BFS());
return 0;
}
深度优先搜索DFS(一)的更多相关文章
- 深度优先搜索DFS和广度优先搜索BFS简单解析(新手向)
深度优先搜索DFS和广度优先搜索BFS简单解析 与树的遍历类似,图的遍历要求从某一点出发,每个点仅被访问一次,这个过程就是图的遍历.图的遍历常用的有深度优先搜索和广度优先搜索,这两者对于有向图和无向图 ...
- 利用广度优先搜索(BFS)与深度优先搜索(DFS)实现岛屿个数的问题(java)
需要说明一点,要成功运行本贴代码,需要重新复制我第一篇随笔<简单的循环队列>代码(版本有更新). 进入今天的主题. 今天这篇文章主要探讨广度优先搜索(BFS)结合队列和深度优先搜索(DFS ...
- 深度优先搜索DFS和广度优先搜索BFS简单解析
转自:https://www.cnblogs.com/FZfangzheng/p/8529132.html 深度优先搜索DFS和广度优先搜索BFS简单解析 与树的遍历类似,图的遍历要求从某一点出发,每 ...
- 【算法入门】深度优先搜索(DFS)
深度优先搜索(DFS) [算法入门] 1.前言深度优先搜索(缩写DFS)有点类似广度优先搜索,也是对一个连通图进行遍历的算法.它的思想是从一个顶点V0开始,沿着一条路一直走到底,如果发现不能到达目标解 ...
- 深度优先搜索 DFS 学习笔记
深度优先搜索 学习笔记 引入 深度优先搜索 DFS 是图论中最基础,最重要的算法之一.DFS 是一种盲目搜寻法,也就是在每个点 \(u\) 上,任选一条边 DFS,直到回溯到 \(u\) 时才选择别的 ...
- 深度优先搜索(DFS)
[算法入门] 郭志伟@SYSU:raphealguo(at)qq.com 2012/05/12 1.前言 深度优先搜索(缩写DFS)有点类似广度优先搜索,也是对一个连通图进行遍历的算法.它的思想是从一 ...
- 算法总结—深度优先搜索DFS
深度优先搜索(DFS) 往往利用递归函数实现(隐式地使用栈). 深度优先从最开始的状态出发,遍历所有可以到达的状态.由此可以对所有的状态进行操作,或列举出所有的状态. 1.poj2386 Lake C ...
- HDU(搜索专题) 1000 N皇后问题(深度优先搜索DFS)解题报告
前几天一直在忙一些事情,所以一直没来得及开始这个搜索专题的训练,今天做了下这个专题的第一题,皇后问题在我没有开始接受Axie的算法低强度训练前,就早有耳闻了,但一直不知道是什么类型的题目,今天一看,原 ...
- [LeetCode OJ] Word Search 深度优先搜索DFS
Given a 2D board and a word, find if the word exists in the grid. The word can be constructed from l ...
- 广度优先(bfs)和深度优先搜索(dfs)的应用实例
广度优先搜索应用举例:计算网络跳数 图结构在解决许多网络相关的问题时直到了重要的作用. 比如,用来确定在互联网中从一个结点到另一个结点(一个网络到其他网络的网关)的最佳路径.一种建模方法是采用无向图, ...
随机推荐
- Springboot中的事件Event
事件Event作为一种常用的线程通讯工具,在Springboot中可以方便地提供开发者进行线程交互. 1.事件定义 1 import org.springframework.context.Appli ...
- [C# 基础知识系列]专题七: 泛型深入理解(一) (转载)
引言: 在上一个专题中介绍了C#2.0 中引入泛型的原因以及有了泛型后所带来的好处,然而上一专题相当于是介绍了泛型的一些基本知识的,对于泛型的性能为什么会比非泛型的性能高却没有给出理由,所以在这个专题 ...
- git教程:工作区和暂存区
Git和其他版本控制系统如SVN的一个不同之处就是有暂存区的概念. 先来看名词解释. 工作区(Working Directory) 就是你在电脑里能看到的目录,比如我的learngit文件夹就是一个工 ...
- linux 路由表 的一些相关资料
linux 路由表维护 查看 Linux 内核路由表 使用下面的 route 命令可以查看 Linux 内核路由表. # route Destination Gateway Genmask Flags ...
- ckeditor_学习(2) 功能概览
这篇文章用来说明 ckeditor 的所有可配置的功能,分为终端用户配置和开发者配置 1.终端用户配置 用户接口 – 设置编辑器的UI和语言 Editor 尺寸设置 – 设置编辑器的尺寸 插入内容 – ...
- webpack根据开发与生产环境配置不同变量--webpack.DefinePlugin
webpack有一个DefinePlugin接口,可以实现根据开发与生产环境配置不同变量.范例如下: 需求:开发环境请求baseUrl = '':生产环境请求 baseUrl = 'http://lo ...
- 20155219付颖卓《网络对抗》Exp6 信息搜集与漏洞扫描
基础问题回答 1.哪些组织负责DNS,IP的管理? 全球根服务器均由美国政府授权的ICANN统一管理,负责全球的域名根服务器.DNS和IP地址管理. 全球根域名服务器:绝大多数在欧洲和北美(全球13台 ...
- liunx学习笔记
告知-----------------------------------grub启动时滚动的代码屏默认我们执行命令使用的为bash,unix使用的为csh能够通过service 程序名进行start ...
- 上手d3js
0---什么是d3js: d3js是一个开源的,基于对svg操作的数据可视化框架,简单的说他提供了数据提供了一系列的数据可视化工具,可以用他很方便的创造出关于svg的动画:svg动画具有可伸缩,不失真 ...
- node中的事件发射器
在事件环中node通过on和emit进行事件的接收和发射,笔者以简单的窗口聊天小demo来演示一下如何通过事件环来发射和监听事件并执行回掉: var events=require('events') ...
