LP-KPN 网络结构

　　

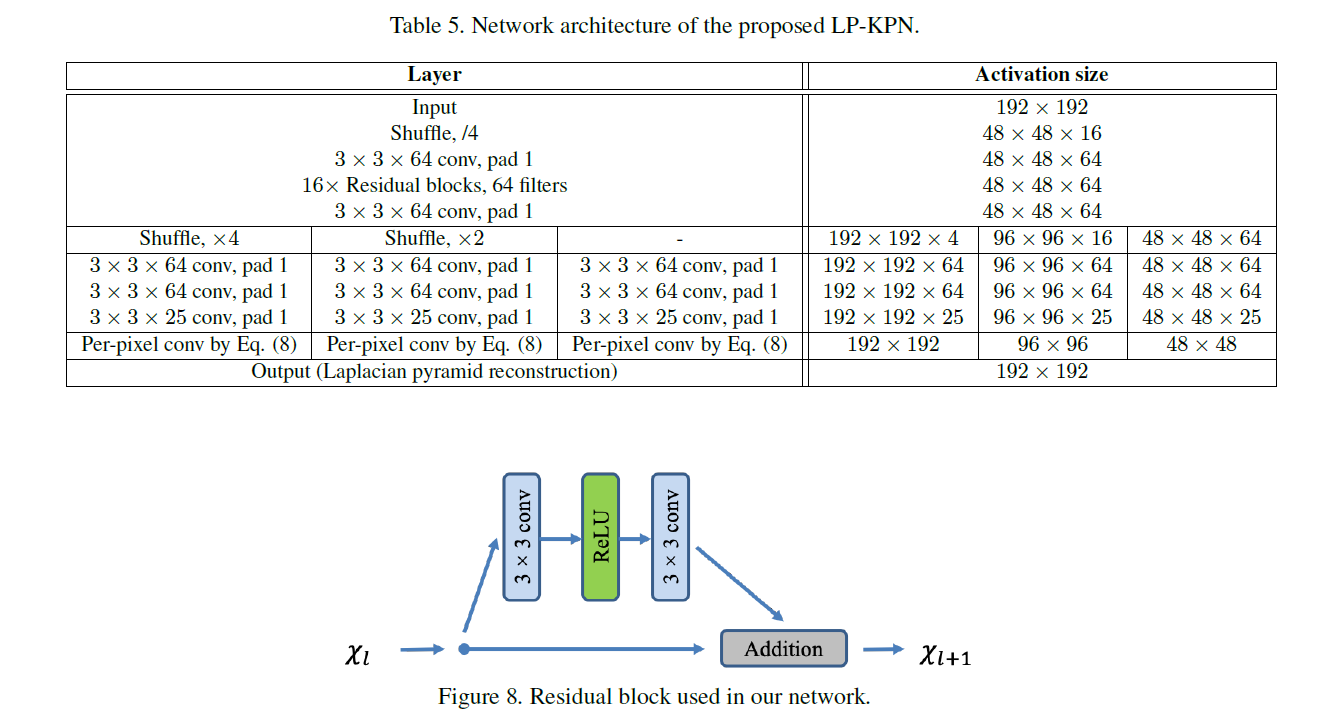
网络解析

1. 网络结构中绿色星星标志 公式。其实就是用预测出来的核在原图片经过Laplacian pyramid decomposes 后的图片上进行卷积运算。所以应该使用padding

2.文章中，该模型是在YCbCr空间上的Y通道实验的

3.最后的Laplacian pyramid restore 过程，应该是使用 Laplacian pyramid unsample （作者没明写，但不是sub-pixel shuffle 网络结构中并未体现）

4.作者提到由于LP的网络结构，使得学习的k*k核等效于4k*4k的核，这减少了参数量

实验参数

1.使用adam训练

2.lr  = 1e-4，训练1000K次迭代

3.对于核k的大小，作者在实验中讨论，不一定大的核获取更棒的性能。

实验

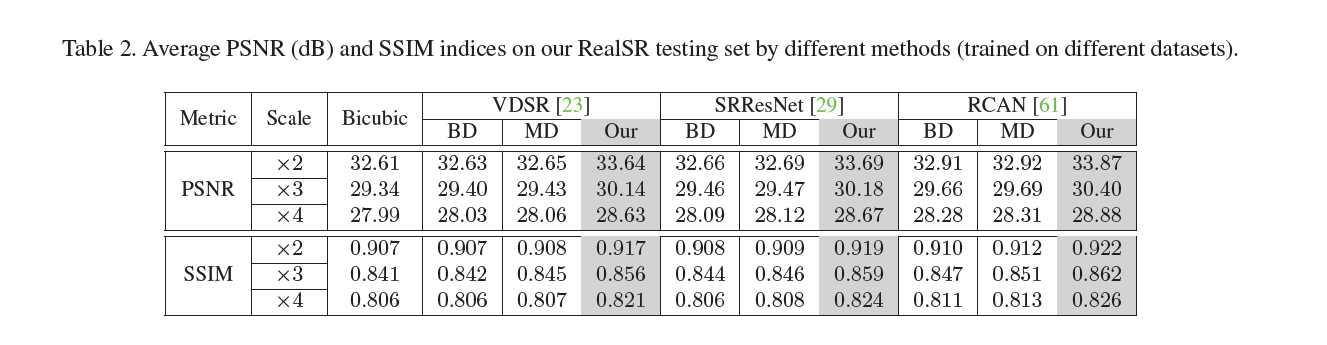
实验1：训练数据集的对比，为了展现Real-SR数据集能提高超分辨率的性能，作者使用DIV2K用过BD（bicubic degradation）和MD（multiple degradation）去生成LR，然后用比较流行的模型去训练

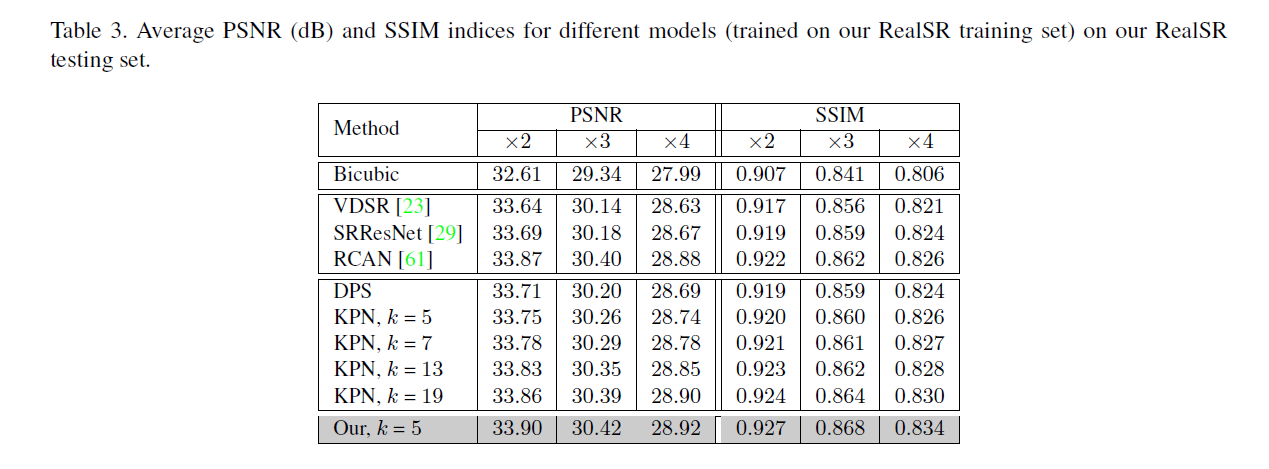
实验2：证明LP-KPN模型性能：通过对比过去的模型，LP-KPN不仅参数量少而且性能也最好，这里也提出核大小为5比KPN核为19更棒，这是由于LP-KPN的结构

LP-KPN的更多相关文章

  1. 对偶理论、拉格朗日对偶问题、LP线性规划对偶性质

    Lagrange 对偶问题 定义其的对偶问题: Lagrange函数 考虑线性规划问题 若取集合约束D={x|x≥0},则该线性规划问题的Lagrange函数为 线性规划的对偶问题为: 对偶定理原问题 ...

  2. [原创] 使用LP Wizard 10.5 制作 Allegro PCB封装

    本文只讲述使用 Calculator 和 Wizard 功能制作封装,通常学会使用这种方法,通用的标准封装就都可以生成了.下面以一个简单的SOIC-8封装的芯片来说明软件使用方法. 第一步,查找相关d ...

  3. 压缩感知中的lp球：p范数最优化为什么总会导致一个稀疏的解的原因

    转自:彬彬有礼. 压缩感知中的lp球:p范数最优化为什么总会导致一个稀疏的解的原因 http://blog.csdn.net/jbb0523/article/details/40268943 题目: ...

  4. 关于LP Wizard生成Allegro封装无焊盘的解决方案

    最近在学Allegro,安装了软件后看网上说LP Wizard可以一键生成Allegro封装,就想去尝尝鲜.毕竟一直都是手动做封装,没怎么用过向导.但是按照网上教程用LP生成了一个封装,发现打开时没有 ...

  5. Linux基础命令---lp打印文件

    lp lp指令用来打印文件,也可以修改存在的打印任务.使用该指令可以指定打印的页码.副本等. 此命令的适用范围:RedHat.RHEL.Ubuntu.CentOS.Fedora.openSUSE.SU ...

  6. Lp空间

    在数学中,Lp空间是由p次可积函数组成的空间:对应的ℓp空间是由p次可和序列组成的空间.它们有时叫做勒贝格空间,以昂利·勒贝格命名(Dunford & Schwartz 1958,III.3) ...

  7. 什么是VC、PE、LP、GP？

    天使基金主要关注原创项目构思和小型初创项目,投资规模大多在300万元以下:风险投资关注初创时期企业长期投资,规模在1000万元以下:私募股权投资主要关注3年内可以上市的成熟型企业. VC即ventur ...

  8. LP线性规划求解 之 单纯形 算法

    LP线性规划求解 之 单纯形 算法 认识-单纯形 核心: 顶点旋转 随机找到一个初始的基本可行解 不断沿着可行域旋转(pivot) 重复2,直到结果不能改进为止 案例-过程 以上篇的case2的松弛型 ...

  9. LP线性规划初识

    认识LP 线性规划(Linear Programming) 特指目标函数和约束条件皆为线性的最优化问题. 目标函数: 多个变量形成的函数 约束条件: 由多个等式/不等式形成的约束条件 线性规划: 在线 ...

  10. 线对 Line pairs、LP（分辨率cy/mm）

    线对 (Line pairs) 是胶片.镜头等电影摄影领域的专用名词. 每毫米线对一般指分辨率的单位,指仪器在一毫米内能分辨出多少对线. 在一定尺度内的可分辨线对数常被用来衡量仪器的空间分辨能力,能分 ...

随机推荐

  1. 全是Bug

    一.开始实现程序之前 1. 在文章开头给出结对使用的Github项目地址和结对伙伴的作业地址.(两个人使用同一个) 我的结对伙伴是 : 201731044205. 伙伴的作业地址: https://w ...

  2. 使用Object.prototype.toString.call()方法精确判断对象的类型

    在JavaScript里使用typeof判断数据类型,只能区分基本类型,即:number.string.undefined.boolean.object. 对于null.array.function. ...

  3. HTML5_canvas_像素操作_图片马赛克_图片反相

    canvas 像素操作 像素,即像素点,一个像素只有一个颜色 100*100 的 px 的屏幕区域有 100*100*4 个像素点,即 width*height*4 rgba(0, 0, 0, 1); ...

  4. [LeetCode] Champagne Tower 香槟塔

    We stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so ...

  5. centos7 部署vnc

    不做过多介绍了,下面直接记录下centos7系统下安装配置vncserver的操作记录 0)更改为启动桌面或命令行模式 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 ...

  6. windows 启动停止 java进程

    本案例以 xxx.jar    为列子 我们一般启动的jar 在任务管理器中查看进程都是javaw.exe ,无法用命令来 kill,所以我们得给自己的java 进程设置个新 title 1:  首先 ...

  7. Linux 部署 xxl-job 注意问题

    问题:Failed to create parent directories for [/data/applogs/xxl-job/xxl-job-admin.log][原因:权限不足] 启动终端: ...

  8. html/jsp导出pdf格式的几种方法（jsPDF，iText，wkhtmltopdf）

    在许多生成报表的时候需要我们后台作出动态的数据,并渲染到前端生成pdf格式,Excel格式的各种报表,但是浏览器自带的生成pdf功能,windows系统的ctrl+p键就能完全搞定这一需求,但对客户来 ...

  9. Fiddler忽略捕捉大文件流

    Fiddler是款非常不错的抓包软件,可以方便的捕捉各种软件发起的HTTP请求,甚至可以在发送给服务器前或响应给应用前修改数据.但是在使用时发现,在开启Fiddler时,在浏览器中下载文件时不会马上弹 ...

  10. iTerm2 与 Oh My Zsh的配套使用

    详见: https://www.jianshu.com/p/7de00c73a2bb https://github.com/sirius1024/iterm2-with-oh-my-zsh https ...