Pytoch机器学习乱玩(一):数学建模作业,体重与心率

动物心率与体重的模型

动物消耗的能量p主要用于维持体温，而体内热量通过其表面积S散失，记动物体重为w，则\(P \propto S \propto w^{\alpha}\)。又\(P\)正比于血流量\(Q\)，而\(Q=wr\),其中\(q\)是动物每次心跳泵出的血流量，\(r\)为心率。假设\(q\)与\(r\)成正比，于是\(P \propto wr\)。于是有\(r \propto w^{\alpha-1}=w^a\),有\(r=kw^a+b\)。

import numpy as np
import matplotlib.pyplot as plt
import torch
import math
%matplotlib inline
r=np.array([[670],[420],[205],[120],[85],[70],[72],[38]])
w=np.array([[25],[200],[2000],[5000],[30000],[50000],[70000],[450000]])
plt.plot(w,r,'bo')
x_sample = np.arange(85, 450000, 0.1)
bottom_range = [1,2,3,4,5]
color = ['red','green','pink','black','blue']
for i in range(5):
    y_sample = 5000*x_sample**(-1/bottom_range[i])
    plt.plot(x_sample, y_sample, color[i],label='real curve')

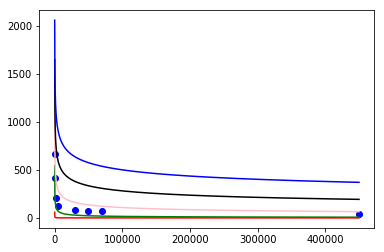
由上图的预模拟，考虑\(r\)的指数为\(-1\),\(-\frac{1}{2}\),\(-\frac{1}{3}\),\(-\frac{1}{4}\),\(-\frac{1}{5}\),从中选取误差最小的

from torch.autograd import Variable
from torch import nn
from torch import optim
import math

#生成目标函数 构建数据集
x_train = w
x_train = torch.from_numpy(x_train).float()
x_train = Variable(x_train)

y_train = torch.from_numpy(r).float()
y_train = Variable(y_train)

#构建模型
class poly_model(nn.Module):
    def __init__(self,bottom):
        super(poly_model,self).__init__()
        self.k = nn.Parameter(torch.randn(1))
        self.b = nn.Parameter(torch.zeros(1))
        self.bottom = bottom

    def forward(self,x):
        out = (x)**(-1/self.bottom)*self.k+self.b
        return out

for i in range(5):
    print("exponential is -1/%d"%(bottom_range[i]))
    model = poly_model(bottom_range[i])
    criterion = nn.MSELoss()
    optimizer = optim.SGD(model.parameters(),lr=1e-3)

    # 更新参数
    for j in range(150000):
        output = model(x_train)
        loss = criterion(output,y_train)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if(j%50000 == 0):
            print(loss.item())
        if(loss.item() < 1e-3): break

    print(model.parameters())
    y_pred = model(x_train)

    plt.plot(x_train.data.numpy()[:, 0], y_pred.data.numpy(), label='fitting curve', color=color[i])
    plt.plot(w, r, label='real curve', color='orange')

经过150000轮预训练，我们得到如下图，表中为曲线颜色对应的指数

指数	颜色	误差
-1/1	红	41184
-1/2	绿	10599
-1/3	粉	1195
-1/4	黑	360
-1/5	蓝	468

其中误差最小的项为\(-\frac{1}{4}\)

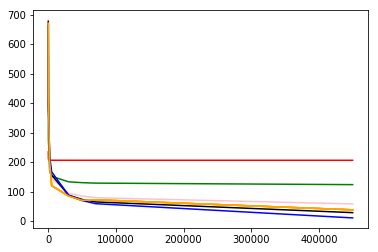
这里可以做一些交叉熵验证找一个最佳的learning rate代码就不贴了 随机生成学习率即可，经过100次验证 我得到的最佳学习率是0.20485，收敛的很快

model = poly_model(4)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(),lr=0.20485)
for j in range(50001):
    output = model(x_train)
    loss = criterion(output,y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if(j%50000 == 0):
        print(loss.item())
y_pred = model(x_train)
plt.plot(x_train.data.numpy()[:, 0], y_pred.data.numpy(), label='fitting curve', color=color[i])
plt.plot(w, r, label='real curve', color='orange')

打印模型参数

param = list(model.parameters())
print(param)

[Parameter containing:
tensor([1591.8446], requires_grad=True), Parameter containing:
tensor([-33.6434], requires_grad=True)]

通过交叉验证，使用0.20485的学习率学习50000轮后，最终模型为\(r=1591.84w^{-\frac{1}{4}}-33.64​\)，均方误差为304.288

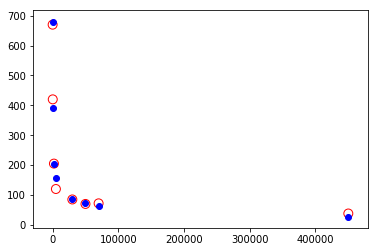
动物	实际心率	预测心率	偏差
田鼠	670	680	+10
家鼠	420	390	-30
兔	205	204	-1
小狗	120	155	+35
大狗	85	87	+2
羊	70	72	+2
人	72	63	-9
马	38	27	-11