[LeetCode] Split BST 分割二叉搜索树

Given a Binary Search Tree (BST) with root node root, and a target value V, split the tree into two subtrees where one subtree has nodes that are all smaller or equal to the target value, while the other subtree has all nodes that are greater than the target value.  It's not necessarily the case that the tree contains a node with value V.

Additionally, most of the structure of the original tree should remain.  Formally, for any child C with parent P in the original tree, if they are both in the same subtree after the split, then node C should still have the parent P.

You should output the root TreeNode of both subtrees after splitting, in any order.

Example 1:

Input: root = [4,2,6,1,3,5,7], V = 2
Output: [[2,1],[4,3,6,null,null,5,7]]
Explanation:
Note that root, output[0], and output[1] are TreeNode objects, not arrays.

The given tree [4,2,6,1,3,5,7] is represented by the following diagram:

          4
        /   \
      2      6
     / \    / \
    1   3  5   7

while the diagrams for the outputs are:

          4
        /   \
      3      6      and    2
            / \           /
           5   7         1

Note:

1. The size of the BST will not exceed 50.
2. The BST is always valid and each node's value is different.

这道题给了我们一棵二叉搜索树Binary Search Tree，又给了我们一个目标值V，让我们将这个BST分割成两个子树，其中一个子树所有结点的值均小于等于目标值V，另一个子树所有结点的值均大于目标值V。这道题最大的难点在于不是简单的将某条边断开就可以的，不如题目中给的那个例子，目标值为2，我们知道要断开结点2和结点4的那条边，但是以结点2为root的子树中是有大于目标值2的结点的，而这个结点3必须也从该子树中移出，并加到较大的那个子树中去的。为了具体的讲解这个过程，这里借用官方解答贴中的例子来说明问题吧。

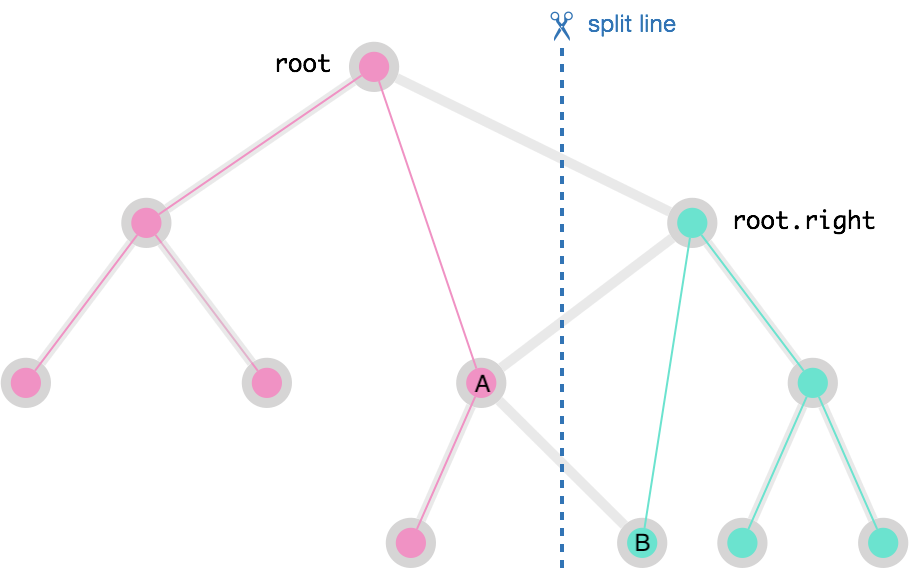
比如对于上图，假如root结点小于V，而root.right大于V的话，那么这条边是要断开的，但是如果root.right的左子结点（结点A）是小于V的，那么其边也应该断开，如果如果root.right的左子结点的右子结点（结点B）大于V，则这条边也应该断开，所以总共有三条边需要断开，如图中蓝色虚线所示，三条粗灰边需要断开，粉细边和绿细边是需要重新连上的边。那么我们应该如何知道连上哪条边呢？不要急，听博主慢慢道来。

博主告诉你们个秘密（一般人我不告诉他），对于树的题目，二话别说，直接上递归啊，除非是有啥特别要求，否则递归都可以解。而递归的精髓就是不断的DFS进入递归函数，直到递归到叶结点，然后回溯，我们递归函数的返回值是两个子树的根结点，比如对结点A调用递归，返回的第一个是A的左子结点，第二个是结点B，这个不需要重新连接，那么当回溯到root.right的时候，我们就需要让root.right结点连接上结点B，而这个结点B是对结点A调用递归的返回值中的第二个。如果是在左边，其实是对称的，root.left连接上调用递归返回值中的第一个，这两个想通了后，代码就不难谢啦，参见代码如下：

class Solution {
public:
    vector<TreeNode*> splitBST(TreeNode* root, int V) {
        vector<TreeNode*> res{NULL, NULL};
        if (!root) return res;
        if (root->val <= V) {
            res = splitBST(root->right, V);
            root->right = res[];
            res[] = root;
        } else {
            res = splitBST(root->left, V);
            root->left = res[];
            res[] = root;
        }
        return res;
    }
};

类似题目：

Delete Node in a BST

参考资料：

https://leetcode.com/problems/split-bst/solution/

https://leetcode.com/problems/split-bst/discuss/113798/C++Easy-recursion-in-O(n)

LeetCode All in One 题目讲解汇总(持续更新中...)