codeforce465DIV2——D. Fafa and Ancient Alphabet

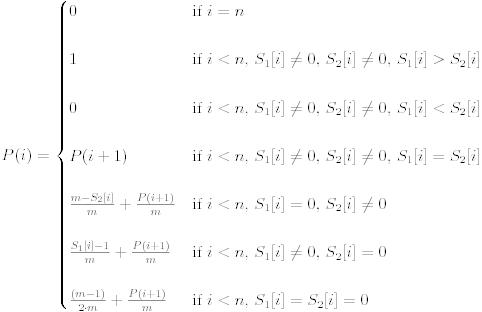
概率的计算答案给出的这张图很清楚了，然后因为要求取模，a/b%M=a*b^-1%M=a*inv(b,M)%M;

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <cstdio>

 using namespace std;
 const int maxn=+;
 const int MOD=;
 typedef long long LL;
 int n,m;
 int s1[maxn],s2[maxn],d[maxn];
 void gcd(LL a,LL b,LL &d,LL &x,LL &y){
     if(!b){
         d=a;x=;y=;
     }else{
         gcd(b,a%b,d,y,x);
         y-=x*(a/b);
     }
 }
 LL inv(LL a,LL n){
     LL d,x,y;
     gcd(a,n,d,x,y);
     return d==?(x+n)%n:-;
 }
 LL dp(int a){
     if(a==n+)return ;
     if(s1[a]==s2[a]&&s1[a]!=&&s2[a]!=)return dp(a+);
     if(s1[a]>s2[a]&&s1[a]!=&&s2[a]!=)return ;
     if(s1[a]<s2[a]&&s1[a]!=&&s2[a]!=)return ;
     if(s1[a]==&&s2[a]!=)
     return (((m-s2[a])%MOD*inv(m,MOD))%MOD+dp(a+)%MOD*inv(m,MOD))%MOD;
     if(s1[a]!=&&s2[a]==)
     return (((s1[a]-)%MOD*inv(m,MOD))%MOD+(dp(a+))%MOD*inv(m,MOD))%MOD;
     if(s1[a]==&&s2[a]==)
     return (((m-)%MOD*inv(*m,MOD))%MOD+(dp(a+)%MOD*inv(m,MOD)))%MOD;
 }

 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)scanf("%d",&s1[i]);
     for(int i=;i<=n;i++)scanf("%d",&s2[i]);
     LL P=dp();
     cout<<P;
 return ;
 }