openGL 变换06
变换
使用(多个)矩阵(Matrix) 对象可以更好的变换(Transform)一个物体。
向量
向量最基本的定义就是一个方向。
或者说 向量有一个方向(Direction)和大小(Magnitude,也叫做强度或长度)。
向量可以在任意纬度(Dimension)上 ,但是我们通常只使用2至4维。
如果一个向量有两个纬度,它表示一个平面的方向(想象一下2D的图像),当它有3个纬度的时候它可以表达一个3D世界的方向。
下面图片会看到3个向量,每个向量在2D图像中都用一个箭头(x,y)表示。我们在2D图片中展示这些向量,因为这样子会更直观一点。
你可以把这些2D向量当做z坐标为0的3D向量。
由于向量表示的是方向,起始于何处并不会改变它的值。
下图我们可以

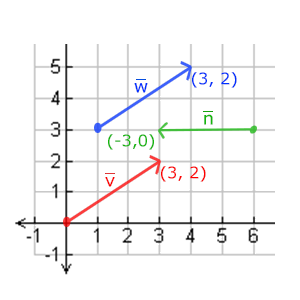

由于向量是一个方向,所以有些时候会很难形象地将它们用位置(Position)表示出来。
为了让其更为直观,我们通常设定这个方向的原点为(0,0,0),然后指向一个方向,对应一个点,使其变为位置向量(Position Vector)
也可以把起点设置为其他的点,然后说:这个向量从这个点起始指向另一点)。比如说位置向量(3,5)在图像中的起点会是(0,0),并会指向(3,5)。
我们可以使用向量在2D或3D空间中表示方向与位置。
向量与标量运算
标量(Scalar)只是一个数字(或者说是仅有一个分量的向量)。
当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。
对于加法来说会像这样:
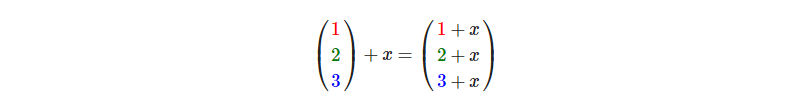
其中的+可以是+、-、.或÷,其中 . 是乘号。注意- 和 ÷ 运算时不能颠倒(标量 -/÷ 向量),因为颠倒的运算是没有定义的。
向量取反
对一个向量取反(Negate)会将其方向逆转。一个指向东北的向量取反后就指向西南方向了。
我们在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量):
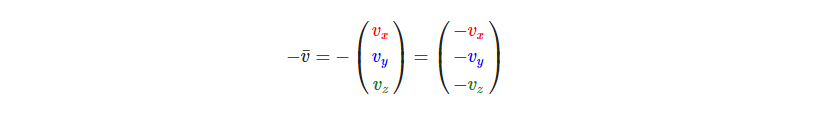
向量与向量加减
向量的加法可以被定义为是分量的(Component-wise)相加,即将一个向量中的每一个分量加上另一个向量的对应分量:
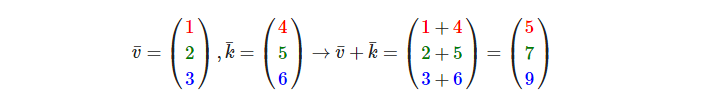
向量v = (4,2)和k =(1,2)可以直观地表示为:
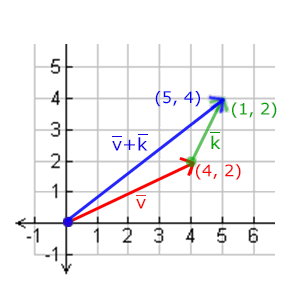
就像普通数字加减一样,向量的减法等于加上第二个向量的相反向量:
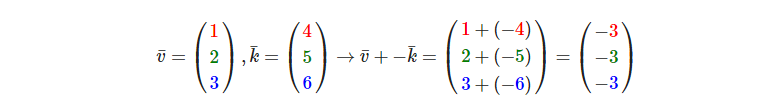
两个向量的相减会得到这两个向量指向位置的差。这在我们想要获取两点的差会非常有用。
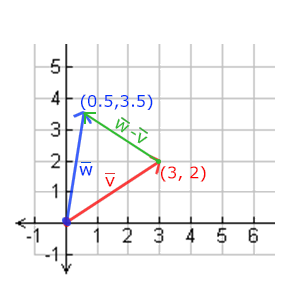
长度
我们使用勾股定理(Pythagoras Theorem) 来获取向量的长度(Length)/大小(Magnitude)。
如果把向量的x与y分量画出来、该向量会和x与y分量为边形成一个三角形:
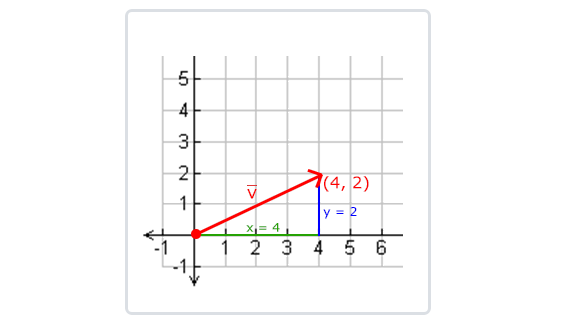
因为两条边(x和y)是已知的,如果希望知道 ,我们可以直接通过勾股定理来计算:
,我们可以直接通过勾股定理来计算:

有一个特殊类型的向量叫做单位向量(Unit Vector)。
单位向量一个特别的性质-------它的长度是1。
我们可以用任意向量的每个分量除以向量的长度得到它的单位向量。
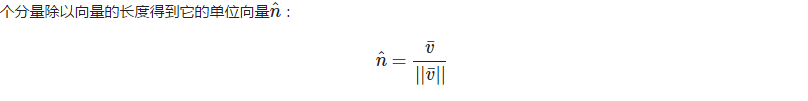
我们把这种方法叫做一个向量的标准化(Normalizing)。单位向量头上有一个^样子的记号。
通常单位向量会变得很有用,特别是我们只关心方向不关心长度的时候(如果改变向量的长度,它的方向并不会改变)。
向量相乘
两个向量相乘是一种很奇怪的情况。
普通的乘法在向量上是没有定义的,因为它在视觉上是没有意义的。
但是在相乘的时候我们有两种特定情况可以选择:

点乘
两个向量的点乘等于它们的数乘结果乘以两个向量之间的余弦值。下面是公式:

现在点积只定义了两个向量的夹角。
90度的余弦值是0,0度的余弦值是1。
使用点乘可以很容易测试两个向量是否正交(Orthogonal)或平行(正交意味着两个向量互为直角)。
如果想要多了解正弦或余弦函数的知识可以看教程:可汗学院的基础三角学视频。
也可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的长度之积,得到的结果就是夹角的余弦值
通过上面点乘定义式可推出:

所以,我们该如何计算点乘呐?点乘是通过将对应分量逐个相乘,然后再把所得积相加来计算的。
两个单位向量的点乘会像是这样:
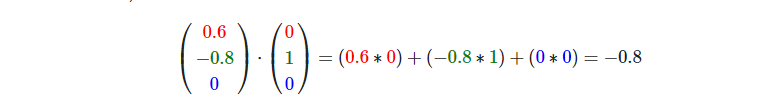
点乘会在计算光照的时候非常有用。
叉乘
叉乘只在3D空间中有定义,它需要两个不平行向量作为输入,生成一个正交于两个输入向量的第三个向量。
如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。
下面图片展示了3D空间中叉乘的样子:
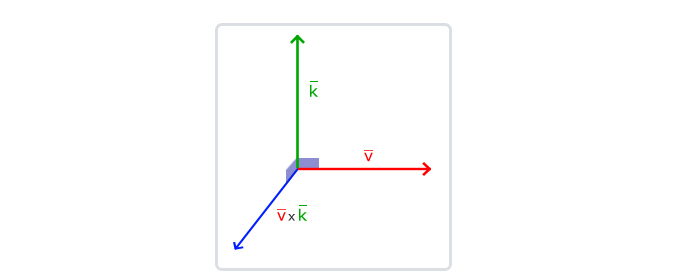
下面你会看到两个正交向量A和B叉积:

只要按照步骤来,就能得到一个正交于两个输入向量的第三个向量。
矩阵
简单来说矩阵就是一个矩形的数字、符号或表达式数组。
矩阵中每一项叫做矩阵的元素(Element)。
下面是一个2x3矩阵的例子:
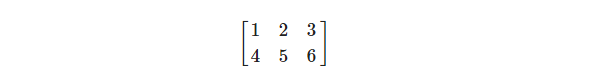
矩阵可以通过(i,j)进行索引,i是行,j是列,这就是上面的矩阵叫做2x3矩阵的原因(3列2行,也叫做矩阵的纬度(Dimension))。
这与你在索引2D图像时的(x,y)相反,获取4的索引是(2,1)(第二行,第一列)(注:如果是图像索引应该是(1,2),先算列、再算行)。
它就是一个矩形的数学表达式阵列。和向量一样,矩阵也有非常漂亮的数学属性。
矩阵有几个运算,分别是:矩阵的加法、减法和乘法。
矩阵的加减
矩阵与标量之间的加减定义如下:
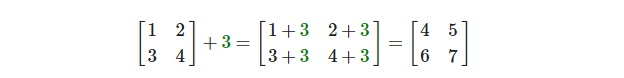
标量值要加到矩阵的每一个元素上。矩阵与标量的减法也相似:

矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算,所以总体的规则和与标量运算是差不多的,
只不过在相同索引下的元素才能进行运算。这也就是说加减法只对同纬度的矩阵才是有定义的。
一个3x2矩阵和一个2x3矩阵(或一个3x3矩阵与4x4矩阵)是不能进行加减的。
两个2x2矩阵是怎么相加的:
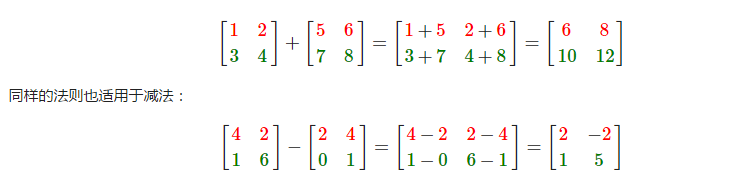
openGL 变换06的更多相关文章
- OpenGL变换【转】
http://www.cnblogs.com/hefee/p/3811099.html OpenGL变换 概述 OpenGL变换矩阵 实例:GL_MODELVIEW矩阵 实例:GL_PROJECTIO ...
- OpenGL变换
概述 OpenGL变换矩阵 实例:GL_MODELVIEW矩阵 实例:GL_PROJECTION矩阵 概述 OpenGL管线中,在光栅化操作之前,包括顶点位置与法线向量的几何数据经顶点操作与图元装配操 ...
- OpenGL学习进程(12)第九课:矩阵乘法实现3D变换
本节是OpenGL学习的第九个课时,下面将详细介绍OpenGL的多种3D变换和如何操作矩阵堆栈. (1)3D变换: OpenGL中绘制3D世界的空间变换包括:模型变换.视图变换.投影变换和视口 ...
- SharpGL学习笔记(七) OpenGL的变换总结
笔者接触OpenGL最大的困难是: 经常调试一份代码时, 屏幕漆黑一片, 也不知道结果对不对,不知道如何是好! 这其实就是关于OpenGL"变换"的基础概念没有掌握好, 以至于对& ...
- OpenGL chapter4 基础变换
math3d库有两个数据类型,能够表示一个三维或四维向量: M3DVector3f M3DVector4f 4.3 理解投影 正投影 : 正交变换 透视投影 : 透视变换 表4.1 OpenGL变换术 ...
- SCARA——OpenGL入门学习五六(三维变换、动画)
OpenGL入门学习(五) 此课为三维变换的内容,比较枯燥.主要是因为很多函数在单独使用时都不好描述其效果, 在前面绘制几何图形的时候,大家是否觉得我们绘图的范围太狭隘了呢?坐标只能从-1到1,还只能 ...
- OpenGL基础图形编程(八)变换
八.OpenGL变换 OpenGL变换是本篇的重点内容,它包含计算机图形学中最主要的三维变换,即几何变换.投影变换.裁剪变换.视口变换,以及针对OpenGL的特殊变换概念理解和使用方法,如相机模拟.矩 ...
- OpenGL入门学习 教程 (五)三维的空间变换
http://oulehui.blog.163.com/blog/static/796146982011924428755/ 在前面绘制几何图形的时候,大家是否觉得我们绘图的范围太狭隘了呢?坐标只能从 ...
- OpenGL ES教程系列(经典合集)
为了搞透播放器的开发,花了些时间收集这些资料,虽然我已经搞定opengles渲染视频的内容,但是想玩玩opengles,往深里玩,图像处理这块是个好的方向,所以opengles是值得好好学的. O ...
随机推荐
- IE中iframe兼容性问题
在使用iframe的时候,有时候想要让调用的iframe框架里面的不显示白背景,让它变得透明,在firefox是透明的,但是在IE浏览器却不透明. 这个其实比较容易解决,只需要增加一个属性即可. 就是 ...
- git pull VS git fetch&merge
使用git fetch和git pull都可以更新远程仓库的代码到本地,但是它们之间还是有区别. git fetch git fetch origin master git log -p maste ...
- 3天学习完AngularJS基础内容小结
简介:AngularJS 是一个 JavaScript 框架.它是一个以 JavaScript 编写的库. 一.AngularJS大致功能模块 二.页面交互变得简单 1.示例:计算价格 <htm ...
- Android spannableStringBuilder用法整理
Android spannableStringBuilder用法整理 分类: Android开发2013-11-29 10:58 5009人阅读 评论(0) 收藏 举报 Androidspannabl ...
- HihoCoder 1097 Prim算法
1097 : 最小生成树一·Prim算法 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 最近,小Hi很喜欢玩的一款游戏模拟城市开放出了新Mod,在这个Mod中,玩家可以 ...
- CMCC有限的访问权限如何解决
最近两天一直出现这个问题,连接CMCC-EDU的时候就是连接不上,提示有限的访问权限,什么诊断和修复IP自动获取都不管用,就是连接不上.怎么说本人也是一个电脑迷,越到这样不靠谱的问题确实不知道如何解决 ...
- webpack新版本4.12应用九(配置文件之入口和上下文(entry and context))
entry 对象是用于 webpack 查找启动并构建 bundle.其上下文是入口文件所处的目录的绝对路径的字符串. context string 基础目录,绝对路径,用于从配置中解析入口起点(en ...
- C#网络编程(接收文件) - Part.5
这篇文章将完成 Part.4 中剩余的部分,它们本来是一篇完整的文章,但是因为上一篇比较长,合并起来页数太多,浏览起来可能会比较不方便,我就将它拆为两篇了,本文便是它的后半部分.我们继续进行上一篇没有 ...
- Android蓝牙UUID简要
UUID是"Universally Unique Identifier"的简称,通用唯一识别码的意思.对于蓝牙设备,每个服务都有通用.独立.唯一的UUID与之对应.也就是说,在同一 ...
- Linux环境下安装jenkins
废话不多说,直接开始 1.从官网下载Jenkins的war包 2.下载好的War放到Tomcat的网站根目录webapps下,然后启动Tomcat. 3.打开浏览器,输入http://IP:8080/ ...
