洛谷 P1182 数列分段`Section II`【二分答案】

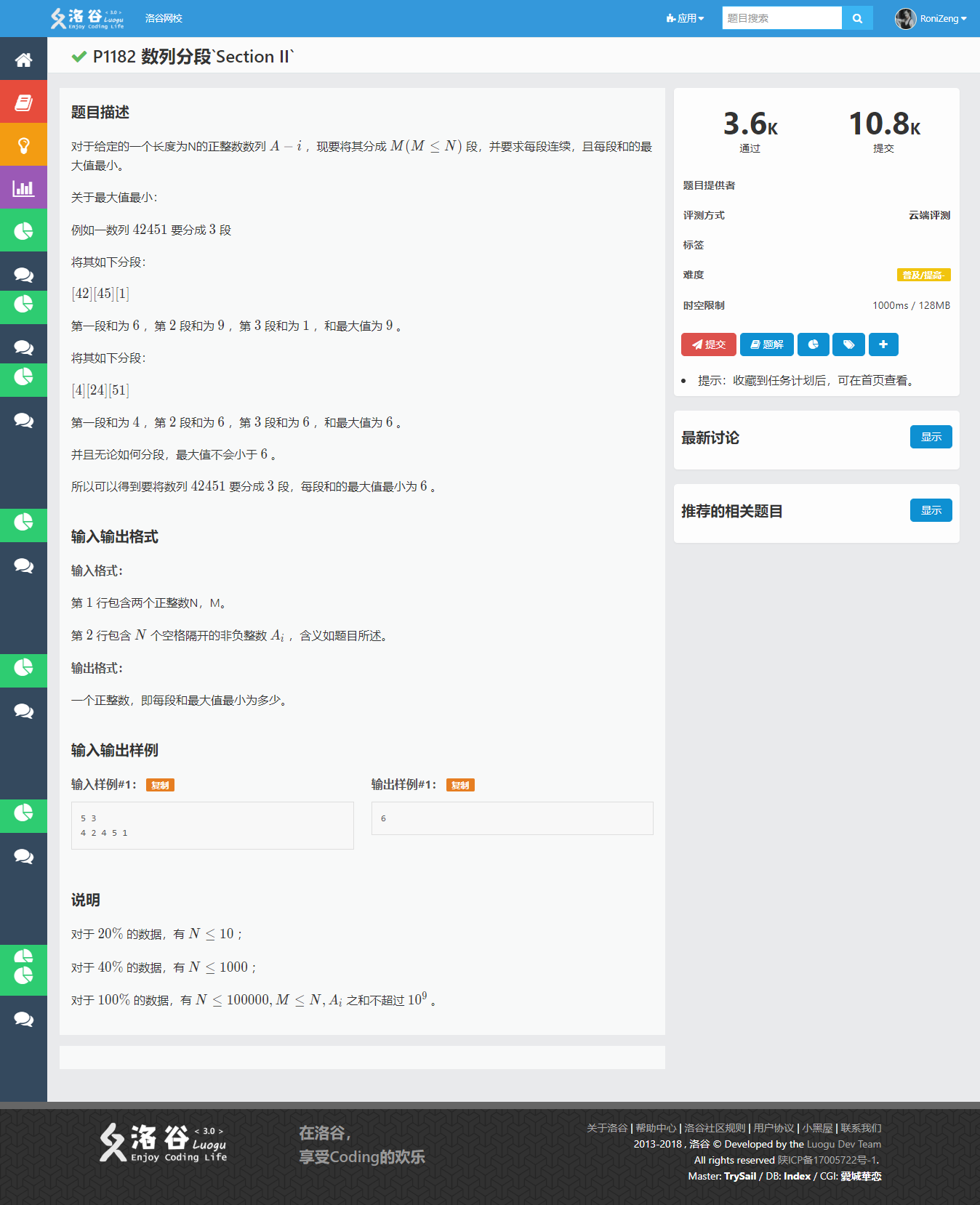
【代码】：

#include<bits/stdc++.h>

const double eps = 1e-8;
const int maxn = 1e6+5;
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;
int n,m;
int a[maxn];

int check(int x)
{
    int sum = 0, cnt = 1;//r是划分的段数，所以要从1开始（相当于植树问题啦）
    for(int i=1; i<=n; i++)
    {
        if(sum+a[i] > x)
        {
            sum = a[i];
            cnt++;
        }
        else sum+=a[i];
    }
    return cnt > m;
}
int slove(int L,int R)
{
    int mid,ans;
    while(L<=R)
    {
        mid = (L+R)/2;
        if(check(mid)) L = mid + 1;
        else R = mid - 1,ans=mid;
    }
    return ans;
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        int L=0,R=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            L = max(L, a[i]);
            R += a[i];
        }
        cout<<slove(L,R)<<endl;
    }
}
/*
5 3
4 2 4 5 1
6
*/