洛谷P4207 [NOI2005]月下柠檬树（计算几何+自适应Simpson法）

题面

传送门

题解

我还好奇自适应辛普森法干嘛用的呢……突然想起来积分的一个用处就是求曲边图形的面积……

我们先来考虑一下这些投影是什么形状

一个圆的投影还是它自己

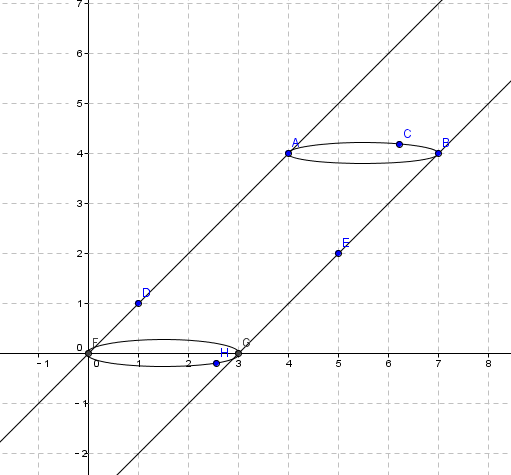
一个圆锥的投影是一个圆加上一个点，以及这个点和圆的两条切线（如果点在圆内部就没有这两条切线）

一个圆台的投影是两个圆加上它们的公切线

最后这个鬼畜的图形大概是长这个样子

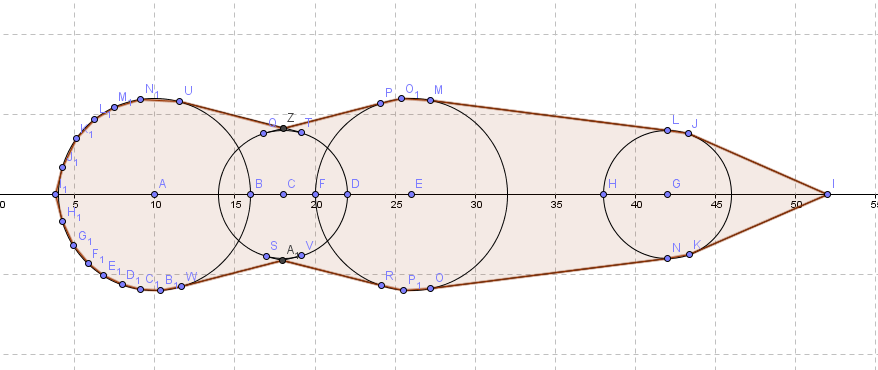
暴力求解即可

我们可以看做这是一个鬼畜的函数，我们要求它在这一段上的积分，那么就是这个封闭图形的面积了，自适应辛普森法即可

//minamoto
#include<bits/stdc++.h>
#define R register
#define sqr(x) ((x)*(x))
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=1005;const double eps=1e-6;
struct node{double x,y;node(){}node(R double xx,R double yy):x(xx),y(yy){}}p;
struct cir{double x,r;cir(){}cir(R double xx,R double rr):x(xx),r(rr){}}C[N];
struct line{
	node s,t;double k,b;
	line(){}
	line(R node ss,R node tt):s(ss),t(tt){k=(t.y-s.y)/(t.x-s.x),b=t.y-t.x*k;}
	inline double f(R double x){return k*x+b;}
}L[N];
int n,tot;double h[N],ll=1e9,rr,ta,alp,x,r,a,b;
void add(const R cir &s,const R cir &t){
	R double si=(s.r-t.r)/(t.x-s.x),co=sqrt(1-sqr(si)),ta=si/co;
	++tot;
	L[tot].s=node(s.x+s.r*si,s.r*co),L[tot].t=node(t.x+t.r*si,t.r*co),
	L[tot].k=-ta,L[tot].b=L[tot].t.y-L[tot].t.x*L[tot].k;
}
double F(R double x){
	R double res=0;
	fp(i,1,tot)(x>=L[i].s.x&&x<=L[i].t.x)?cmax(res,L[i].f(x)):0;
	fp(i,1,n)(x>=C[i].x-C[i].r&&x<=C[i].x+C[i].r)?cmax(res,sqrt(sqr(C[i].r)-sqr(x-C[i].x))):0;
	return res;
}
double simpson(R double l,R double r){return (F(l)+F(r)+4*F((l+r)/2))*(r-l)/6;}
double calc(double l,double r,double eps,double res){
	double mid=(l+r)/2,ql=simpson(l,mid),qr=simpson(mid,r);
	if(fabs(ql+qr-res)<=15*eps)return ql+qr+(ql+qr-res)/15;
	return calc(l,mid,eps/2,ql)+calc(mid,r,eps/2,qr);
}
int main(){
//	freopen("testdata.in","r",stdin);
	scanf("%d%lf",&n,&alp),ta=tan(alp);
	fp(i,1,n+1)scanf("%lf",&h[i]),h[i]+=h[i-1];
	fp(i,1,n)scanf("%lf",&C[i].r),C[i].x=h[i]/ta;
	p=node(h[n+1]/ta,0),x=C[n].x,r=C[n].r;
	cmax(rr,p.x),cmax(rr,x+r),cmin(ll,x-r);
	if(p.x>x+r)a=sqr(r)/(p.x-x),b=sqrt(sqr(r)-sqr(a)),L[++tot]=line(node(x+a,b),p);
	fd(i,n-1,1){
		cmax(rr,C[i].x+C[i].r),cmin(ll,C[i].x-C[i].r);
		if(C[i+1].x-C[i].x>fabs(C[i+1].r-C[i].r))add(C[i],C[i+1]);
	}
	printf("%.2lf\n",2*calc(ll,rr,eps,simpson(ll,rr)));
	return 0;
}