斯坦福机器学习视频笔记 Week7 支持向量机 Support Vector Machines

SVM被许多人认为是最强大的“黑箱”学习算法，并通过提出一个巧妙选择的优化目标，今天最广泛使用的学习算法之一。

Optimization Objective

根据Logistic Regression，有如下表述：

为了达到尽量好的分类效果，我们需要theta‘*x >> 0 or theta‘*x << 0，根据上面的函数图象，这时候的h(x)->1 or h(x)->0,可以看出这时我们的分类效果是最具说服力的。

根据逻辑回归的Cost Function我们可以得到上面灰色的函数图像，

if y=1，随着z的增大，Cost Function的值趋近于0；

if y=0，随着z的减小，Cost Function的值趋近于0；

在SVMs中，为了使分类结果更具说服力（使y等于0，1的概率更大），我们将使用上面的玫瑰色的函数轨迹替代灰色轨迹，把它们分别称为cost1(y=1)和cost0(y=0)，

可以看到，它们二者的很类似，除了当Z>=1时，使Cost Function等于0（y=1时）；当Z<=-1时，使Cost Function等于0（y=0时）。

当然，这里你也可以将等于0的点设置为其他数据，比如z>=2,3等，视你的系统情况而定，z>=1不是硬性规定。

逻辑回归的Cost Function:

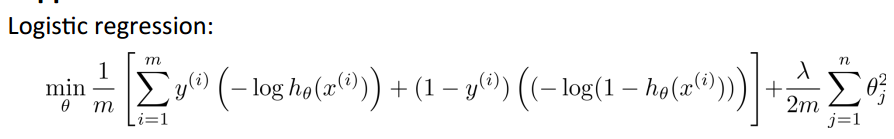
根据逻辑回归的Cost Function，我们得到SVM的Cost Function：

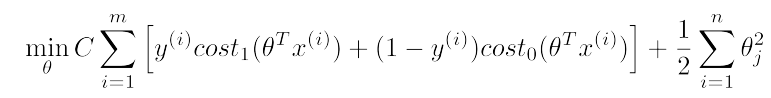
和上面的公式相比，SVM的Cost Function的两项都去掉的1/m，这个不会影响我们求最优值，因为最值和函数系数无关；

多了一个C，少了一个lambda，这个可以理解为C = 1/lambda，关于参数C后面还会讲到。

Large Margin Intuition

上面的图，是我们之前谈论的一个总结。在SVM中，我们使用上面的损失函数，且使theta'*x>=1时取y=1，而不再是像逻辑回归中的仅仅是theta'*x>=0；当y=0时，是一个意思。

为了方便研究我们的最优化目标，将C取一个很大的值，比如C=100，000，为了得到最小的Cost Function值，我们记上面方框中的式子为 W ，则必须使W的式子取值趋于0，

W有两项组成，当y=1时，此时W就只有第一项，根据之前cost1的图像可知，此时只需要取theta‘*x>=1就可使Cost Function等于0；y=0时，同理使theta‘*x<=-1可使Cost Function等于0。

然后我们的最优化目标将可简化为：

Large Margin

我们称SVM为“Large Margin Classifier“，下面将体现最大间隔：

这里给的样本是线性可分的，直观上来看，这里的粉色和绿色的都不是最大间隔，而是黑线，蓝色线是与最近的样本点相近的黑线的平行线。

下面给出一个非线性可分的样本，

当C很大时，SVM是严格的分类器，此时将严格划分样本点，可以看出此时的间隔已经非常不好了，上图红色的。

当C不是很大时，SVM可以允许有一定的噪声点，此时会直接忽略，得到一个看上去不错的分类间隔，上图黑色的。

The'mathematics' behind'large'margin' classification'(optional) 

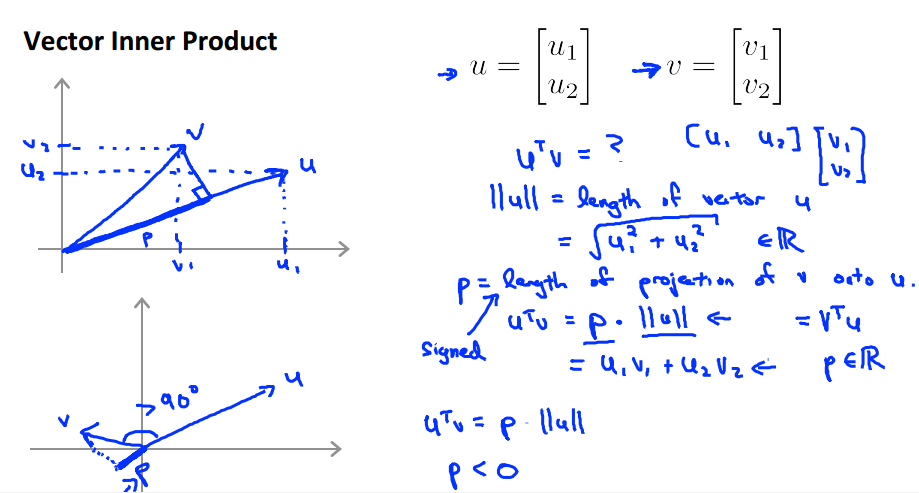
首先，在这里我假设大家都知道向量内积和向量投影。

上面的基本意思就是，向量u和v计算内积，p是向量v在向量u方向上的投影，那么u’*v = p * ||u||=u1*v1+u2*v2.

其中投影p可正可负，是向量具有方向。

同理，将此应用到theta‘*x中去，此时p是x在theta方向上的投影，如下图所示。

上面使用的最优化目标是使C很大时，简化过后的，这样方便讨论。下面的讨论要结合上面和下面的图一起看。

由上面的讨论可知，当y=1时，theta’*x>=1 在这里就等价于 p * ||theta|| >= 1，优化目标变成1/2 * ||theta||^2。

这里我们设theta0=0，这样间隔面会通过原点.下面给一个样本集合，随意画一个间隔平面，将正负类分开。

我们知道间隔面的法向量thea跟它垂直，故x在theta上的投影p就是上图theta方向上的红色有向线段。

可以看出，在上面的情况，绿色的间隔面，此时正样本X的投影p取>0的很小的值，若要满足p * ||theta|| >= 1 的条件，必须使theta变得足够大，这样就跟我们最小化目标1/2*||theta||^2不符合了，所以这个就不是我们所需要的“最大间隔”。在负样本时p取<0的很小值，同样不满足最优化要求。那么最大间隔会是怎样的呢？看下面。

此时的样本的投影P不论在>0or<0时的取值都比较大，所以为了满足p*||theta||>1,此时的theta就可以取较小的值了，就能得到最优化的结果，即为最大间隔。

所以最优的间隔应该是使x的投影p尽可能大。

SVM Kernles

首先我们从下面的非线性决策边界分类说起。

在之前，我们学习过用多项式模型拟合出上面的边界。我们将featuer使用f1，f2，...来表示。

当我们使用多项式模型时，计算成本大大加重，这在图像处理时根本就是无法使用的。

思考一下featuer有没有更好的表示方法呢？下面将介绍基于landmark的方法。

给定的样本x，我们计算其与landmarks（l1，l2，l3）的相近度来确定new feature，上面使用Gaussian Kernels作为相似函数，分别计算f1，f2，f3...

结合上图的分析可知，当样本x与landmark接近时，其f1->1，相反，当x离l很远时，f1->0.计算后的f，将作为new feature。

关于f作以下说明：

f作为图像的z轴的高，最高值为1，该点对应的坐标即为l1，从该点想四周扩散时，f在不断减小直至趋于0.关于参数sigma，是控制f值下降的快慢。

下面来讨论引入new feature的SVM是如何预测分类的。

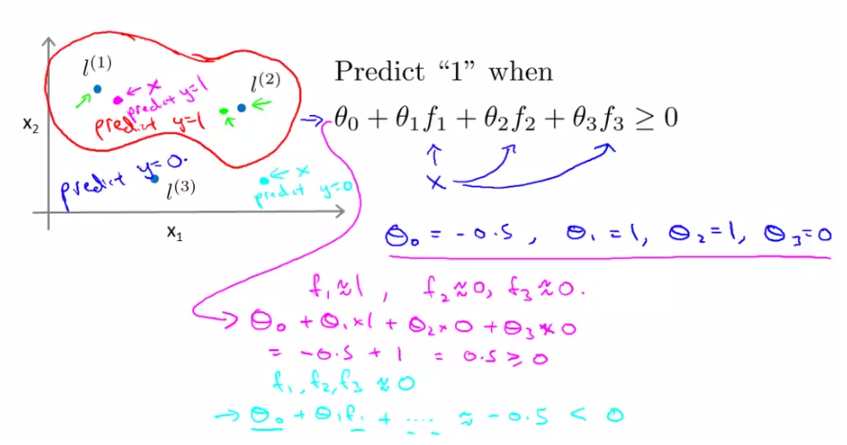
首先根据样本x和landmarks计算f1,f2,f3，假设现在已经训练出了参数theta如上面所示，

则将算的f带入上面的式子，用向量表示为theta‘*f,如果其结果>=0,则预测结果为y=1；结果为<0,则预测结果为y=0。

上面的结果便是，离l1和l2近的点其预测为y=1，即在那个红色的圈内，y=1；在圈外预测y=0.

下面就将说明如何确定landmark和训练theta。

我们把每一个样本都作为landmark，l(1) = x(1),l(2) = x(2),...

然后使用Kernel计算new feature f1，f2,....

其中每个x(i)对应的f(i)，每个f(i)都有一个分量f（i,i）=1,如上图红笔所示，然后设每一个f向量的f(0)=1,这样就得到了new feature的f向量，这里的样本x和f都是(m+1)维的数据。

接下来就是训练theta。

通过最小化上面的Cost Function，便可以得到参数theta，这里使用new feature f 替代x，带入cost1和cost2.

然后就可以使用训练得的theta参数进行分类预测了。if theta’*f >= 0,predict ‘y=1’，otherwise ‘y=0’。

下面是关于SVM参数C和Gaussian Kernels参数sigma的说明。

提示一下，当使用参数C时，请把它看作是逻辑回归中的1/lambda，然后就可以根据lambda来分析bias和variance。

同理，sigma可以看作是高斯分布中的sigma，表示图像的宽度。

Using an SVM

在使用SVM时，请注意图中画框的部分，主要是参数C和Kernel的选择，如果选择Gaussian Kernel就要面临参数sigma的选择。

需要提醒的是，在使用Gaussian Kernel时请务必先进行feature scaling。

另外，除了上面提到的不同的kernel，还有其他的选择，如下。

SVM也可以扩展到多分类，原理和logistics regression相似，都是one-vs-all method，具体可以参考http://www.cnblogs.com/yangmang/p/6352118.html

最后还有一件事，比较一下logistics regression和SVMs。

参考：http://blog.csdn.net/abcjennifer/article/details/7849812