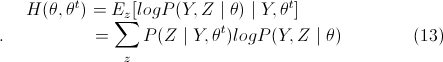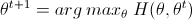EM算法(expectation maximization)
EM算法简述
EM算法是一种迭代算法,主要用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计。EM算法的每次迭代由两步完成:
E步,求期望
M步,求极大。
EM算法的引入
如果概率模型的变量都是观测变量,那么给定数据,可以直接用极大似然估计法或贝叶斯估计法估计模型参数,但是当模型中含有隐变量时,就不能简单地使用这些估计方法。因此提出了EM算法。
EM算法流程
假定集合  由观测数据
由观测数据  和未观测数据
和未观测数据  组成,
组成,  和
和  分别称为不完整数据和完整数据。假设Z的联合概率密度被参数化地定义为
分别称为不完整数据和完整数据。假设Z的联合概率密度被参数化地定义为  ,其中
,其中  表示要被估计的参数。
表示要被估计的参数。  的最大似然估计是求不完整数据的对数似然函数
的最大似然估计是求不完整数据的对数似然函数 的最大值而得到的:
的最大值而得到的: EM算法包括两个步骤:由E步和M步组成,它是通过迭代地最大化完整数据的对数似然函数
EM算法包括两个步骤:由E步和M步组成,它是通过迭代地最大化完整数据的对数似然函数  的期望来最大化不完整数据的对数似然函数,其中:
的期望来最大化不完整数据的对数似然函数,其中: 假设在算法第t次迭代后
假设在算法第t次迭代后  获得的估计记为
获得的估计记为  ,则在(t+1)次迭代时,E-步:计算完整数据的对数似然函数的期望,记为:
,则在(t+1)次迭代时,E-步:计算完整数据的对数似然函数的期望,记为: M-步:通过最大化
M-步:通过最大化  来获得新的
来获得新的  。通过交替使用这两个步骤,EM算法逐步改进模型的参数,使参数和训练样本的似然概率逐渐增大,最后终止于一个极大点。
。通过交替使用这两个步骤,EM算法逐步改进模型的参数,使参数和训练样本的似然概率逐渐增大,最后终止于一个极大点。
直观地理解EM算法,它也可被看作为一个逐次逼近算法:事先并不知道模型的参数,可以随机的选择一套参数或者事先粗略地给定某个初始参数,确定出对应于这组参数的最可能的状态,计算每个训练样本的可能结果的概率,在当前的状态下再由样本对参数修正,重新估计参数λ,并在新的参数下重新确定模型的状态,这样,通过多次的迭代,循环直至某个收敛条件满足为止,就可以使得模型的参数逐渐逼近真实参数。
可见上述算法流程中Q()是EM算法的核心,称为Q函数。
即完整数据的对数似然函数logP(x,y| )关于在给定观测数据x和当前参数
)关于在给定观测数据x和当前参数 下对未观测数据y的条件概率分布P(y|x,
下对未观测数据y的条件概率分布P(y|x, )的期望称为Q函数,
)的期望称为Q函数,
EM算法的导出
我们面对一个含有隐变量的概率模型,目标是极大化观测数据(不完全数据)x关于参数 的对数似然函数,即极大化
的对数似然函数,即极大化
L( )=logP(x|
)=logP(x| )=logΣyP(X,y|
)=logΣyP(X,y| )=log(ΣyP(X|y,
)=log(ΣyP(X|y, )P(y|
)P(y| ))
))
注意到这一极大化主要困难是式中有未观测数据并有包含和(或积分)的对数
示例
给定样本T = {X1, X2, …, Xm},现在想给每个Xi一个Zi,即标出: {(X1,Z1), (X2,Z2),…,(Xm,Zm)}(z是隐形变量,zi=j可以看成是Xi被划分为j类),求对T的最大似然估计:
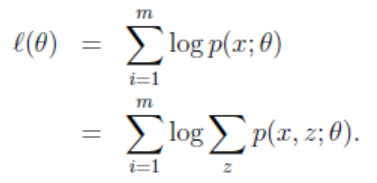
其实Zi也是个向量,因为对于每一个Xi,都有多种分类的情况。设第i个样本Xi在Z上的概率分布为Qi(Zi),即Qi(Zi=j)表示Xi被划分到类j的概率,因此有ΣQi(Zi) = 1。
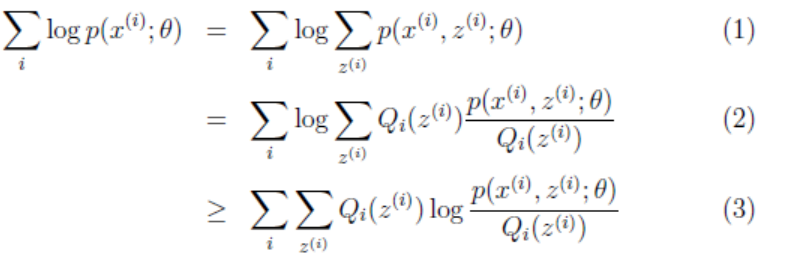
(2)到(3)是利用Jensen不等式,因为log(x)为凹函数,且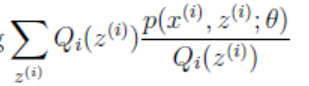 这个就是p(xi, zi; θ)/Qi(zi)的期望。
这个就是p(xi, zi; θ)/Qi(zi)的期望。
现在,根据Jensen不等式取等号的条件:
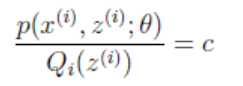
因为这个式子对于Zi等于任何值时都成立,且有ΣQi(Zi) = 1,所以可以认为:Σp(xi, zi;θ) = c。此时可以推出:
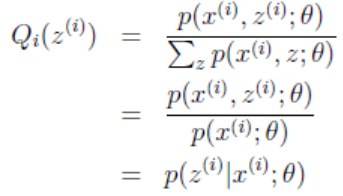
式子中,Zi是自变量,若θ已知,则可计算出Qi(zi)。
至此,终于可以描述算法过程了:
1)给θ一个初始值;
2)固定当前的θ,让不等式(3)取等号,算出Qi(zi);-------> E 步
3)将2)算出的Qi(zi)代入g(Q, θ) = 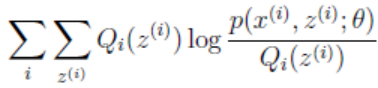 ,并极大化g(Q,θ),得到新的θ。-------------->M步
,并极大化g(Q,θ),得到新的θ。-------------->M步
4)循环迭代2)、3)至收敛。
证明EM算法收敛
当θ取到θt值时,求得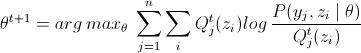
那么可得如下不等式:
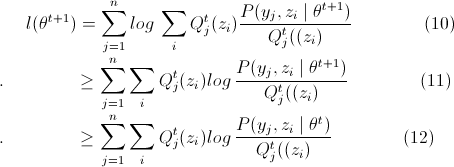
(10)=>(11)是因为Jensen不等式,因为等号成立的条件是θ为θt的时候得到的 ,而现在
,而现在 中的θ值为θt+1,所以等号不一定成立,除非θt+1=θt,
中的θ值为θt+1,所以等号不一定成立,除非θt+1=θt,
(11)=>(12)是因为θt+1已经使得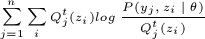 取得最大值,那必然不会小于(12)式。
取得最大值,那必然不会小于(12)式。
所以l(θ)在迭代下是单调递增的,且很容易看出l(θ)是有上界的(单调有界收敛),则EM算法收敛性得证。
EM算法E步说明
上述EM算法描述,主要是参考Andrew NG教授的讲义,如果看过李航老师的《统计方法学》,会发现里面的证明以及描述表明上有些许不同,Andrew NG教授的讲义的说明(如上述)将隐藏变量的作用更好的体现出来,更直观,证明也更简单,而《统计方法学》中则将迭代之间θ的变化罗列的更为明确,也更加准确的描述了EM算法字面上的意思:每次迭代包含两步:E步,求期望;M步,求极大化。下面列出《统计方法学》书中的EM算法,与上述略有不同:
EM算法(2):
选取初始值θ0初始化θ,t=0
Repeat {
E步:
M步:
}直到收敛
(13)式中,Y={y1,y2,...,ym},Z={z1,z2,...,zm},不难看出将(9)式中两个Σ对换,就可以得出(13)式,而(13)式即是关于分布z的一个期望值,而需要求这个期望公式,那么要求出所有的EM算法(1)中E步的值,所以两个表明看起来不同的EM算法描述其实是一样的。
总结:EM算法就是通过迭代地最大化完整数据的对数似然函数的期望,来最大化不完整数据的对数似然函数。
参考文献:
1.《统计学习方法》
2. http://blog.csdn.net/hechenghai/article/details/41896213
3.https://baike.baidu.com/item/em%E7%AE%97%E6%B3%95/1866163?fr=aladdin
EM算法(expectation maximization)的更多相关文章
- EM算法(Expectation Maximization Algorithm)
EM算法(Expectation Maximization Algorithm) 1. 前言 这是本人写的第一篇博客(2013年4月5日发在cnblogs上,现在迁移过来),是学习李航老师的< ...
- EM算法(Expectation Maximization)
1 极大似然估计 假设有如图1的X所示的抽取的n个学生某门课程的成绩,又知学生的成绩符合高斯分布f(x|μ,σ2),求学生的成绩最符合哪种高斯分布,即μ和σ2最优值是什么? 图1 学生成绩的分 ...
- EM算法(Expectation Maximization Algorithm)初探
1. 通过一个简单的例子直观上理解EM的核心思想 0x1: 问题背景 假设现在有两枚硬币Coin_a和Coin_b,随机抛掷后正面朝上/反面朝上的概率分别是 Coin_a:P1:-P1 Coin_b: ...
- 简单理解EM算法Expectation Maximization
1.EM算法概念 EM 算法,全称 Expectation Maximization Algorithm.期望最大算法是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最 ...
- EM 算法 Expectation Maximization
- EM(Expectation Maximization)算法
EM(Expectation Maximization)算法 参考资料: [1]. 从最大似然到EM算法浅解 [2]. 简单的EM算法例子 [3]. EM算法)The EM Algorithm(详尽 ...
- 最大期望算法 Expectation Maximization概念
在统计计算中,最大期望(EM,Expectation–Maximization)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Lat ...
- 机器学习-EM算法
最大期望算法 EM算法的正式提出来自美国数学家Arthur Dempster.Nan Laird和Donald Rubin,其在1977年发表的研究对先前出现的作为特例的EM算法进行了总结并给出了标准 ...
- 数据挖掘十大经典算法(5) 最大期望(EM)算法
在统计计算中,最大期望(EM,Expectation–Maximization)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Lat ...
- EM算法及其推广
概述 EM算法是一种迭代算法,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计. EM算法的每次迭代由两步组成:E步,求期望(expectation): ...
随机推荐
- .htaccess中的apache rewrite规则写法详解(未完)
转:http://www.cnblogs.com/adforce/archive/2012/11/23/2784664.html http://blog.csdn.net/Long_Xiao_Yun/ ...
- GEEK学习笔记— —程序猿面试宝典笔记(三)
所谓笔记,就是比較个人的东西,把个人认为有点意思的东西记录下来~~ 程序猿面试宝典笔记(一)基本概念 程序猿面试宝典笔记(二)预处理.const和sizeof 程序猿面试宝典笔记(三)auto_ptr ...
- MySQL(8)--Cluster 7.4 rpm centos7
还没来得及写.我就知道一个月完毕不了,暂时添加的工作总是拖后腿. .. MySQL集群 docker下安装MySQL Cluster报错了.是我image的包少了perl.老实装吧.image又小不了 ...
- 用brew安装gcc48
由于mac自带的gcc的版本过低,因此想自己装一个新的gcc. 在网上搜索了一圈后发现用brew install安装比较简单,但可能由于本地的brew有冲突,因此网上的攻略都没有效果. 通过在gith ...
- DSP6455的cmd文件
DSP6455的cmd文件 CMD 的专业名称叫链接器配置文件,存放链接器的配置信息,DSP编译器的编译结果是未定位的,DSP也没有操作系统来定位执行代码,DSP系统的配置需求也不尽相同,因此需要定义 ...
- InputArray和OutputArray
源码路径:~/opencv-2.4.9/modules/core/include/opencv2/core/core.hpp where _InputArray is a class that can ...
- html之常用元素
基础: <!DOCTYPE> 定义文档的类型 语法: html5 <!DOCTYPE html> <html> 定义html文档,这个就不多说了! <titl ...
- (初学者)安装hadoop集群注意事项
1.关闭防火墙 2.所有的hadoop操作都是hadoop用户下面的,同时需要用hadoop用户登录之后,对于其他的机器的hadoop用户可以免密登录 3.hadoop用户在root组下面,不是附加组 ...
- ext2文件系统了解
一个磁盘可以划分成多个分区,每个分区必须先用格式化工具(例如mkfs命令)格式化成某种格式的文件系统,然后才能存储文件,格式化的过程会在磁盘上写一些管理存储布局的信息.下以ext2文件系统为例说明文件 ...
- CodeIgniter 框架在Apache服务器下去掉index.php 总结
最近一段时间一直研究CI框架,但是对CI框架的跳转链接一直需要加index.php前缀,经过CI论坛的各种解决方案,最后总结记录一下自己实际操作去掉index.php的过程. 1.要修改Apache ...