Manacher（马拉车）学习笔记

Manacher可以有效的在\(O(n)\)时间内解决一个字符串的回文子串的题目

目录

1. 简介
2. 讲解
3. 推介
4. 简单的练习
5. 恐怖的练习QAQ
6. 小结

简介

开头都说了，Manacher是目前解决回文子串的最有效的方法之一，可以在\(O(n)\)时间内处理出以这个点为中心的最大回文子串长度。

讲解

例题

1. 将偶数的回文子串处理成奇数回文子串

在暴力处理回文子串的过程中，我们会把偶数与奇数的分成两个判断

相信大家一定会有这个疑问，那么，我们在开头、结尾与两两字符中间插入一个没有出现过的字符，如：'#'，举个栗子：aaaa做完处理为：#a#a#a#a#。

那么偶数的回文子串就是以'#'为中心的字符串。

为什么在开头与结尾插入一个'#'，首先，仔细思考：

在#a#a#a#a#不管以哪个字符为中心，枚举到的回文子串的开头与结尾都肯定是'#'号，如：a#a，我们可以在两个a再向外扩展一个'#'。

如果不在开头与结尾加的话，就会出现开头结尾不是'#'的异类回文子串，如a#a。

那么，我们就可以愉快直接算长度为奇数的回文子串了。

2. 统计答案

由于后面的内容会十分的血腥，所以我还是先把简单的搬到前面。

首先，我们定义一个数组ma数组，\(ma_{i}\)代表以\(i\)到以\(i\)为中心的最大回文子串的开头的长度，如：#a#b#b#c#b#，中以\(c\)为中心，组成的最大回文子串为#b#c#b#，c到最右边的#的串长度为4，所以他的\(ma\)就为4！

那么，如何统计答案？

如图：

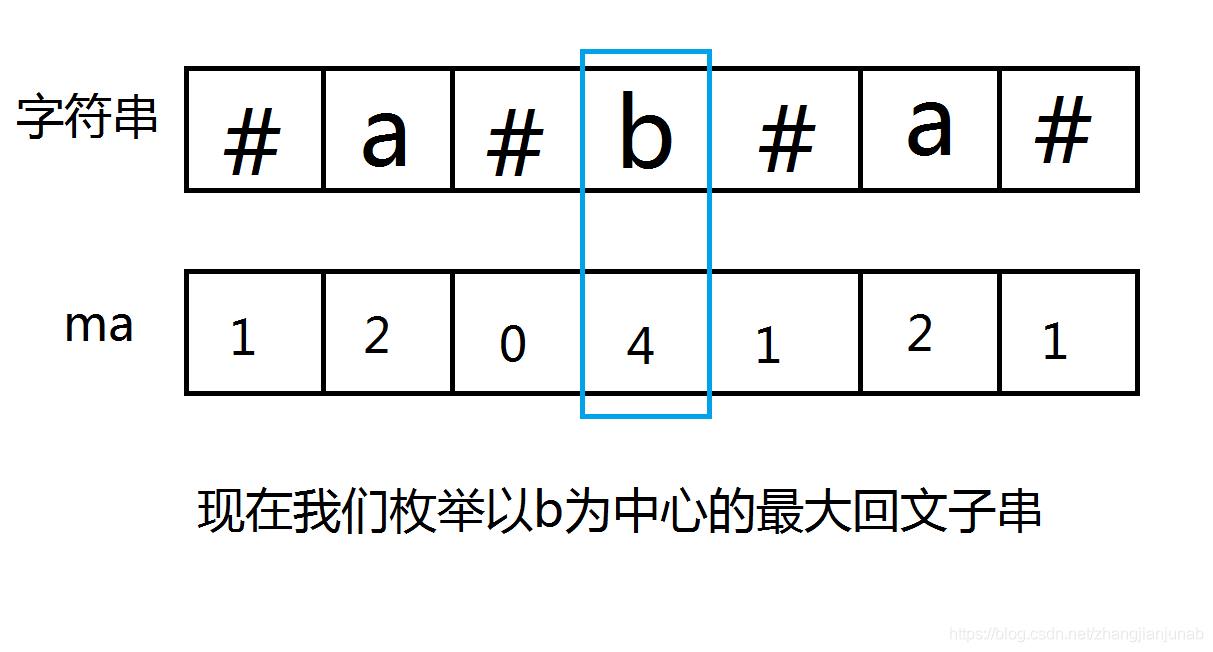
回归正题，我们发现，b的ma值是4，同时真正的回文子串是3（去掉#号），难道就是ma值减1？

没错，就是，为什么？

我们继续思考：把右边的字母与左边的'#'号调转一下

如图：

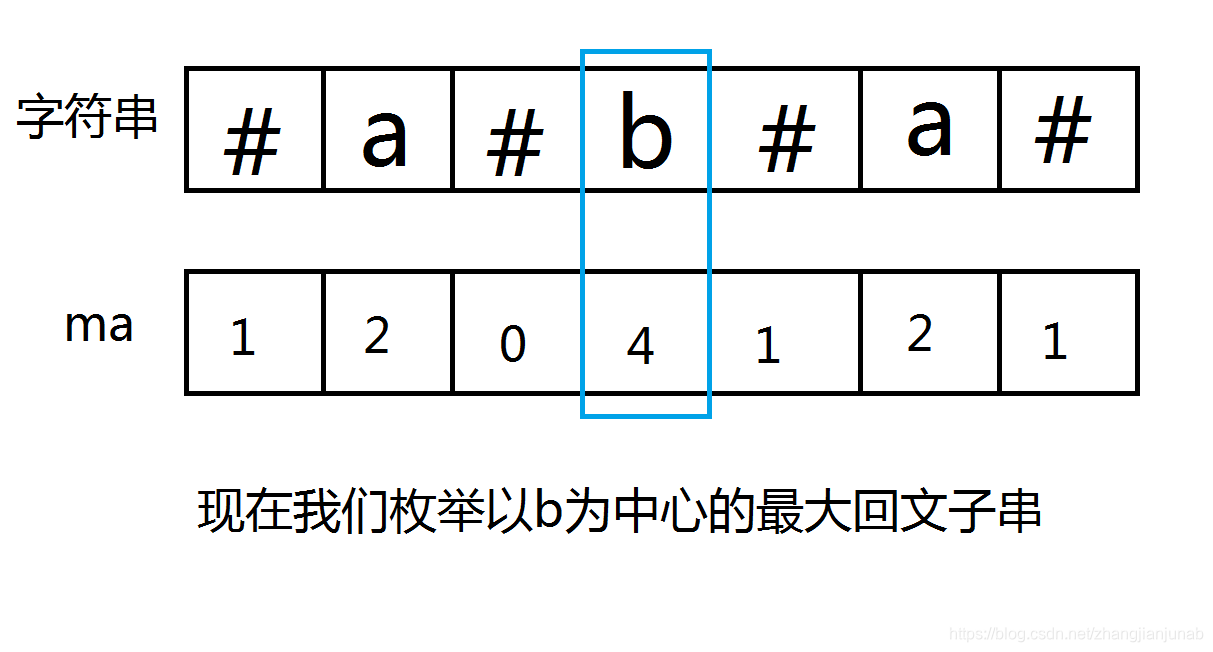
首先，我们知道，目前我们是以字母作为中心而不是'#'， 那么，在回文子串中中心左边的子串就呈现这种情况：#?#?#?#...#（问号是字母），而这个子串的长度是中心的ma值减1，'#'的个数是?的个数加1。

而右边也是#?#?#?#...#（问号是字符），长度也一样，'#'与?的个数也一样，那么把右边的字母与左边的'#'号调转一下，我们会发现右边的子串全是'#'，而左边只剩下一个'#'号。

那么，根据ma数组的定义，以字母为中心的回文子串的长度为ma值减1。

那以'#'为中心的呢？

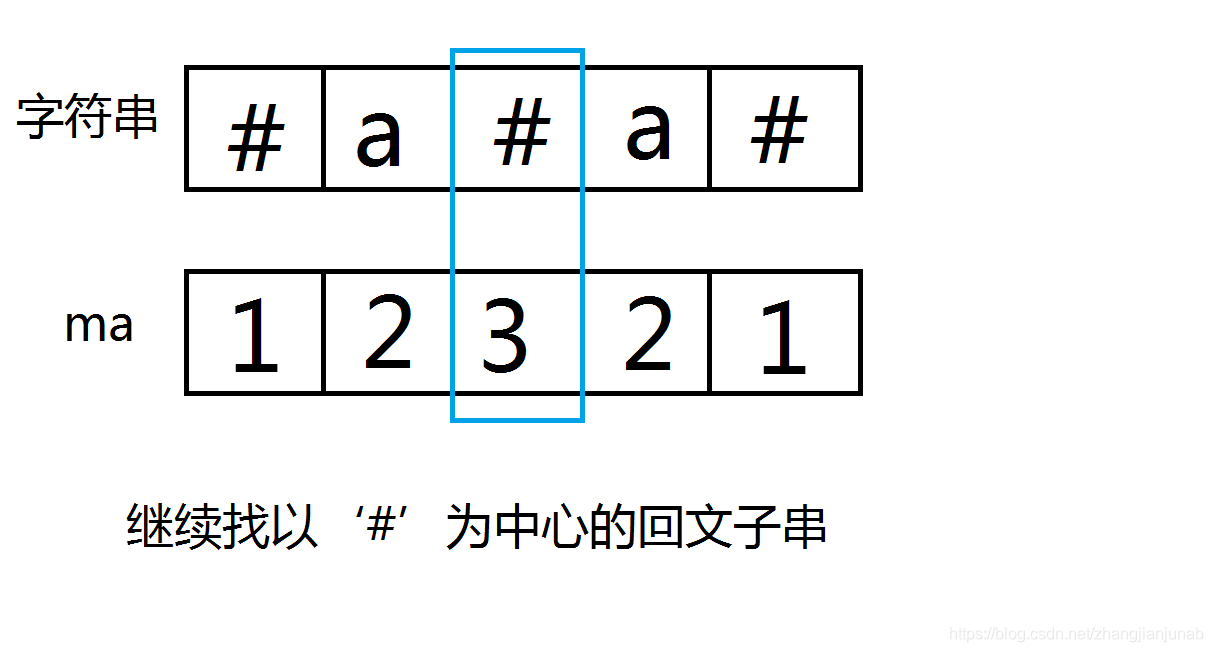
貌似也是ma值减1哟。

继续，如果以#为中心，那么回文子串中心的左边与右边的子串也都是#?#?#?，长度为ma值减1，同时#的个数与?的个数相同，把左边的'#'与右边的'#'交换，那么左边全都是?，而中心是个'#'号，所以也是ma值减1。

处理ma数组

没错，这也是最重要的！

学过EXKMP的话，这个应该是可以自己手推的。

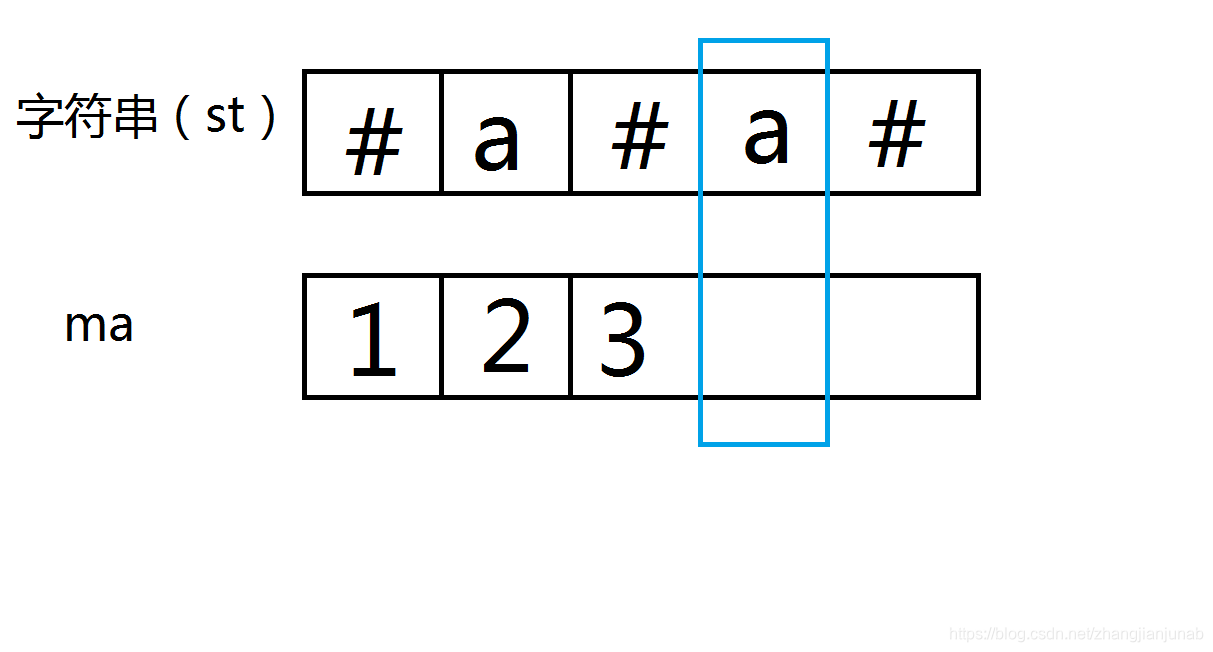
现在处理以a为中心的回文子串，难道还要从1开始？

细心的同学发现了，由于第三个位置（'#'）的ma值为3，我们可以发现，\(st_{2}=st_{4},st_{1}=st_{5}\)，我们可以大胆的猜想一下我们可以将\(ma_{2}\)作为一个参考，\(ma_{2}\)值为2，仔细一看，\(ma_{4}\)的值至少为2！

继续参考EXKMP。

我们得到一下步骤：

1. 统计目前回文子串能到的最远位置(p)与是哪个中心(b)。
2. 设\(L=ma_{b-(i-b)}\)
3. 当\(i+L-1<p\)时，ma的值直接等于L
4. 当\(i+L-1≥p\)时，ma值为\(p-i+1\)，然后开始直接暴力匹配，更新b与p。

其实在\(i+L-1>p 并且 i≤p\)时，ma值其实直接等于\(p-i+1\)就可以了，不需要暴力匹配，跟EXKMP差不多。

至于更改了b与p为什么答案还一样，我就不一一赘述了，都跟EXKMP差不多。

现在都还不懂的话，看代码自行理解吧

#include<cstdio>
#include<cstring>
#define  N  23000000
using  namespace  std;
char  st[N],sst[11000000];
int  ma[N],n,ans;//定义
inline  int  mymax(int  x,int  y){return  x>y?x:y;}
void  Man()
{
    int  b=0,p=0;
    for(int  i=1;i<=n;i++)
    {
        int  L=ma[b-(i-b)];
        if(i+L-1<p)ma[i]=L;//情况1
        else
        {
            int  pp=p-i+1<1?1:p-i+1;//至少为1
            while(i-pp>=1  &&  i+pp<=n  &&  st[i-pp]==st[i+pp])pp++;//(i-pp+1)-1>=1,i+pp-1+1<=n
            ma[i]=pp;b=i;p=ma[b]+b-1;ans=mymax(ans,ma[i]-1);//更新
        }
    }
}
int  main()
{
    scanf("%s",sst+1);n=strlen(sst+1);
    for(int  i=1;i<=n;i++)st[i*2]=sst[i];
    st[n*2+1]='#';for(int  i=1;i<=n;i++)st[i*2-1]='#';//填'#'号
    n=n*2+1;Man();//匹配
    printf("%d\n",ans);
    return  0;
}

推介

在这个OJ上找视频，还可以，以前就是在这学的

例题很多

其实Manacher在学完EXKMP后，在学一点Manacher的概念，就可以手推了，毕竟我也是在历史课上手推的。（应该也归功于以前学过一次）。

总之也挺好理解的，就不一一赘述了。

简单的练习

基本上都是自己会做的。。。

Manacher一大部分的统计题都是\(O(n)\)可以统计，一般到了\(O(n^{2})\)，就不大正常了，简单的例题都是\(O(n)\)可以统计的。

练习1

在Manacher匹配中，统计每个位置为开头或结尾的回文子串最长是多少。

然后在后面在更新全局：\(ll_{i}=mymax(ll_{i},ll_{i-2}-2)\)（跳过'#'），\(rr_{i}=mymax(rr_{i},rr_{i+2}-2)\)（跳过'#'）。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#define  N  210000
using  namespace  std;
char  st[N],stt[N];
int  ma[N],f[N],n,ll[N]/*为开头*/,rr[N]/*为结尾*/,ans;
inline  int  mymax(int  x,int  y){return  x>y?x:y;}
void  Man()
{
    int  b=0,p=0;
    for(int  i=1;i<=n;i++)
    {
        int  L=ma[b-(i-b)];
        if(i+L-1<p)ma[i]=L;
        else
        {
            int  pp=p-i+1<1?1:p-i+1;
            while(i-pp>=1  &&  i+pp<=n  &&  st[i-pp]==st[i+pp])pp++;
            ma[i]=pp;b=i;p=ma[b]+b-1;
        }
        ll[i-ma[i]+2]=ma[i]-1;
        !rr[i+ma[i]-2]?rr[i+ma[i]-2]=ma[i]-1:0;//用贪心来省时间
    }
}
int  main()
{
    scanf("%s",stt+1);n=strlen(stt+1);
    st[n*2+1]='#';for(int  i=1;i<=n;i++)st[i*2]=stt[i],st[i*2-1]='#';
    n=n*2+1;Man();
    for(int  i=2;i<n;i+=2)ll[i]=mymax(ll[i],ll[i-2]-2);
    for(int  i=n-1;i>=2;i-=2)rr[i]=mymax(rr[i],rr[i+2]-2);//后面递推更新
    for(int  i=4;i<=n;i+=2)
    {
        if(rr[i-2]  &&  ll[i])ans=mymax(ans,rr[i-2]+ll[i]);//统计答案
    }
    printf("%d\n",ans);//输出
    return  0;
}

---

练习2

用类似差分统计，然后用快速幂加速一下。

#include<cstdio>
#include<cstring>
#define  N  1100000
#define  mod  19930726
using  namespace  std;
typedef  long  long  ll;
char  st[N];
int  ma[N],n;
ll  sum[N],ans,f[N],k;
void  Man()
{
    f[1]=n;
    int  b=0,p=0;
    for(int  i=1;i<=n;i++)
    {
        int  L=ma[b-(i-b)];
        if(i+L-1<p)ma[i]=L;
        else
        {
            int  pp=p-i+1<1?1:p-i+1;
            while(i-pp>=1  &&  i+pp<=n  &&  st[i-pp]==st[i+pp])pp++;
            ma[i]=pp;b=i;p=ma[b]+b-1;
        }
        f[ma[i]*2+1]--;
    }
}
ll  kpow(ll  x,ll  p)//快速幂
{
    ll  qwq=1;
    while(p)
    {
        if(p%2==1)qwq*=x,qwq%=mod;
        x*=x;p>>=1;x%=mod;
    }
    return  qwq;
}
int  main()
{
    scanf("%d%lld",&n,&k);
    scanf("%s",st+1);
    Man();
    for(int  i=1;i<=n;i+=2)f[i]+=f[i-2];//差分的前缀和。
    ans=1;
    for(int  i=n;i>=1;i--)
    {
    	if((i&1)==0)continue;//不是'#'
        sum[i]=f[i]+sum[i+2];
        if(sum[i]>=k)//达到限制
        {
            ans*=kpow(i,k-sum[i+2]);ans%=mod;
            break;//退出
        }
        if(i==1)//没有
        {
            printf("-1\n");
            return  0;
        }
        ans*=kpow(i,f[i]);ans%=mod;
    }
    printf("%lld\n",ans);//输出
    return  0;
}

---

练习三

同样记录是否是开头或结尾，然后用乘法统计，一个数字乘以一个前缀和而已。

当然还是用了差分。。。

就不多讲了，luogu有题解

//用了与第一题不同的统计方法
#include<cstdio>
#include<cstring>
#define  N  4100
using  namespace  std;
char  st[N],stt[N];
int  ma[N],n,ll[N],rr[N];
long  long  ans;
void  Man()
{
    int  b=0,p=0;
    for(int  i=1;i<=n;i++)
    {
        int  L=ma[b-(i-b)];
        if(i+L-1<p)ma[i]=L;
        else
        {
            int  pp=p-i+1<1?1:p-i+1;
            while(i-pp>=1  &&  i+pp<=n  &&  st[i-pp]==st[i+pp])pp++;
            ma[i]=pp;b=i;p=b+ma[b]-1;
        }
        ll[i-ma[i]+1]++;ll[i]--;rr[i+ma[i]-1]++;rr[i]--;//差分
    }
}
int  main()
{
    scanf("%s",stt+1);n=strlen(stt+1);
    st[1]='#';for(int  i=1;i<=n;i++)st[i*2+1]='#',st[i*2]=stt[i];
    n=n*2+1;Man();//匹配
    for(int  i=1;i<=n;i++)ll[i]+=ll[i-1];
    for(int  i=n;i>=1;i--)rr[i]+=rr[i+1];//先处理每个数的和
    for(int  i=3;i<=n;i+=2)rr[i]+=rr[i-2];//再处理一个的前缀和
    for(int  i=1;i<=n;i+=2)ans+=ll[i]*rr[i];//统计
    printf("%lld\n",ans);
    return  0;
}

---

练习四

这里稍微有些不同，我们不是找两边相等的回文子串，而是找两边相反的回文子串，如：1100。

而且必须是以'#'为中心，首先，按题意理解，回文子串必须是偶数长度的，其二，由于换了回文子串的定义，所以在Manacher的匹配中，以一个数字为中心也会出错，这个很容易想为什么，所以Manacher只找以'#'为中心的情况就是了。

#include<cstdio>
#include<cstring>
#define  N  1100000
using  namespace  std;
char  st[N],stt[N];
int  ma[N],n;
long  long  ans;
void  Man()
{
    int  b=0,p=0;
    for(int  i=1;i<=n;i+=2/*只找'#'号*/)
    {
        int  L=ma[b-(i-b)];
        if(i+L-1<p)ma[i]=L;
        else
        {
            int  pp=p-i+1<1?1:p-i+1;
            while(i-pp>=1  &&  i+pp<=n  &&  (st[i-pp]=='#'?1:st[i-pp]==(st[i+pp]^1)/*不同的计算方法*/))pp++;
            ma[i]=pp;b=i;p=ma[b]+b-1;
        }
        ans+=(ma[i]-1)/2;//统计
    }
}
int  main()
{
    scanf("%d",&n);
    scanf("%s",stt+1);
    st[1]='#';for(int  i=1;i<=n;i++)st[i*2+1]='#',st[i*2]=stt[i];
    n=n*2+1;
    Man();
    printf("%lld\n",ans);
	return  0;
}

---

练习五

用一个数组记录以这个位置为开头的最长不下降子序列的长度。

然后匹配的时候统计答案。

#include<cstdio>
#include<cstring>
#define  N  210000
using  namespace  std;
int  n,st[N],ma[N],f[N],ans;
inline  int  mymin(int  x,int  y){return  x<y?x:y;}//最小值
inline  int  mymax(int  x,int  y){return  x>y?x:y;}//最大值
void  Man()
{
    int  b=0,p=0;
    for(int  i=1;i<=n;i++)
    {
        int  L=ma[b-(i-b)];
        if(i+L-1<p)ma[i]=L;
        else
        {
            int  pp=p-i+1<1?1:p-i+1;
            while(i-pp>=1  &&  i+pp<=n  &&  st[i-pp]==st[i+pp])pp++;
            ma[i]=pp;b=i;p=ma[b]+b-1;
        }
        ans=mymax(mymin(ma[i]-1,f[i]-1),ans);//统计
    }
}
int  main()
{
    int  T;scanf("%d",&T);
    while(T--)
    {
        ans=0;
        scanf("%d",&n);
        st[1]=-1;
        for(int  i=1;i<=n;i++)
        {
            scanf("%d",&st[i*2]);
            st[i*2+1]=-1;
        }
        n=n*2+1;
        //输入
        f[1]=1;
        int  mind=251,minid=0;
        for(int  i=2;i<=n;i+=2)
        {
            if(mind<=st[i])mind=st[i],f[i]=i-minid+2;//包括一个-1
            else  mind=st[i],minid=i,f[i]=2;
            f[i+1]=f[i]+1;//方便后面记录答案
        }//处理最长不下降子序列
        Man();
        printf("%d\n",ans);
    }
    return  0;
}

恐怖的练习

练习一

听说是Hash+Manacher判重，不过不想做了QAQ。

练习二

这个就真的不会了QAQ，好像是Manacher+朴素统计+优化。

小结

Manacher真的是一个不错的算法QMQ