bzoj 1007 凸壳

首先明确一个概念

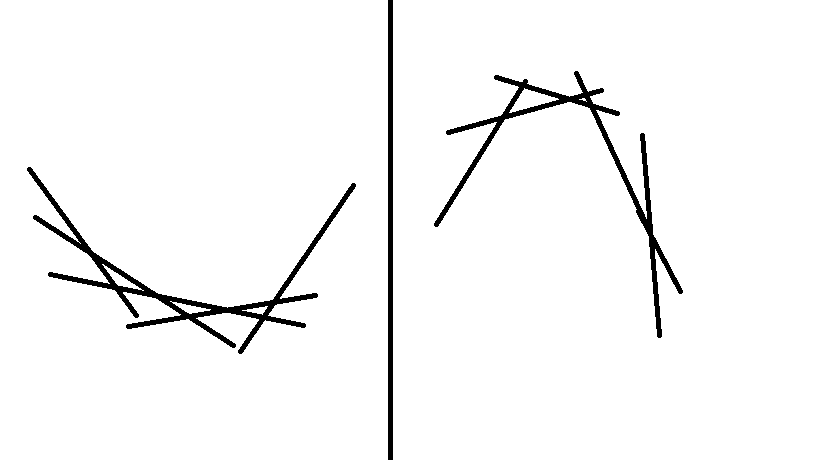
左面内个叫上凸壳，右面那个叫下凸壳

然后我们只需要维护一个上图壳就行了，先按着斜率排序，每次加进来一条边，判断tot边和这个边与tot-1边的交点横坐标，

如果这条边的横坐标小就一直弹栈就好了

/**************************************************************
    Problem:
    User: BLADEVIL
    Language: Pascal
    Result: Accepted
    Time: ms
    Memory: kb
****************************************************************/
 
//By BLADEVIL
var
    n                       :longint;
    a, b, num               :array[..] of longint;
    quea, queb              :array[..] of longint;
    tot                     :longint;
    quex                    :array[..] of double;
    ans                     :array[..] of longint;
    i                       :longint;
     
procedure swap(var a,b:longint);
var
    c                       :longint;
begin
    c:=a; a:=b; b:=c;
end;
     
procedure qs(low,high:longint);
var
    i, j, xx, yy            :longint;
begin
    i:=low; j:=high; xx:=a[(i+j) div ];
    yy:=b[(i+j) div ];
    while i<j do
    begin
        while (a[i]<xx) or (a[i]=xx) and (b[i]>yy) do inc(i);
        while (a[j]>xx) or (a[j]=xx) and (b[j]<yy) do dec(j);
        if i<=j then
        begin
            swap(a[i],a[j]);
            swap(b[i],b[j]);
            swap(num[i],num[j]);
            inc(i); dec(j);
        end;
    end;
    if i<high then qs(i,high);
    if j>low then qs(low,j);
end;
 
procedure qs1(low,high:longint);
var
    i, j, xx                :longint;
begin
    i:=low; j:=high; xx:=ans[(i+j) div ];
    while i<j do
    begin
        while ans[i]<xx do inc(i);
        while ans[j]>xx do dec(j);
        if i<=j then
        begin
            swap(ans[i],ans[j]);
            inc(i); dec(j);
        end;
    end;
    if i<high then qs1(i,high);
    if j>low then qs1(low,j);
end;
     
procedure insert(i:longint);
var
    k                       :longint;
    x                       :double;
begin
    if a[i]=quea[tot] then exit;
    if tot> then
    begin
        x:=(queb[tot-]-b[i])/(a[i]-quea[tot-]);
        while (tot>) and (x<=quex[tot]) do
        begin
            dec(tot);
            x:=(queb[tot-]-b[i])/(a[i]-quea[tot-]);
        end;
    end;
    inc(tot);
    quea[tot]:=a[i];
    queb[tot]:=b[i];
    quex[tot]:=(queb[tot-]-b[i])/(a[i]-quea[tot-]);
    ans[tot]:=num[i];
end;
     
begin
    read(n);
    for i:= to n do read(a[i],b[i]);
    for i:= to n do num[i]:=i;
    qs(,n);
    quea[]:=a[]; queb[]:=b[];
    quex[]:=-maxlongint; ans[]:=num[];
    tot:=;
    for i:= to n do insert(i);
    qs1(,tot);
    for i:= to tot do write(ans[i],' ');
end.