【BZOJ4403】序列统计 Lucas定理

【BZOJ4403】序列统计

Description

给定三个正整数N、L和R，统计长度在1到N之间，元素大小都在L到R之间的单调不降序列的数量。输出答案对10^6+3取模的结果。

Input

输入第一行包含一个整数T，表示数据组数。第2到第T+1行每行包含三个整数N、L和R，N、L和R的意义如题所述。

Output

输出包含T行，每行有一个数字，表示你所求出的答案对106+3取模的结果。

Sample Input

2

1 4 5

2 4 5

Sample Output

25

HINT

提示
【样例说明】满足条件的2个序列为[4]和[5]。
【数据规模和约定】对于100%的数据，1≤N,L,R≤10^9，1≤T≤100，输入数据保证L≤R。

题解：区间[l,r]等价于区间[1,r-l+1]。

设f[i][j]表示i个数，最大的那个数是j的方案数，有

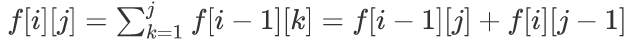
这不就是斜过来的杨辉三角吗？然后我们要求的就是这个东西

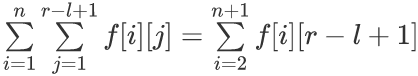
感觉从1开始不太好看，但是反正f[1][...]等于1，于是我们加上一项

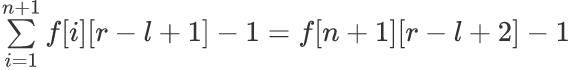
因为这是一个斜过来的杨辉三角，所以f[n+1][r-l+2]对应的就是C[n][n+r-l+1]

然后上lucas定理就行了

注意不能先把1-1000003的逆元都求出来，会TLE！

#include <cstdio>
#include <cstring>
#include <iostream>
#define mod 1000003ll
typedef long long ll;
ll n,m;
ll jc[mod+10],jcc[mod+10];
ll pm(ll x,ll y)
{
	if(jcc[x])	return jcc[x];
	ll z=1;
	while(y)
	{
		if(y&1)	z=z*x%mod;
		x=x*x%mod,y>>=1;
	}
	return jcc[x]=z;
}
ll dfs(ll a,ll b)
{
	if(!b)	return 1;
	if(a<b)	return 0;
	if(a<mod&&b<mod)	return jc[a]*pm(jc[b],mod-2)%mod*pm(jc[a-b],mod-2)%mod;
	return dfs(a%mod,b%mod)*dfs(a/mod,b/mod)%mod;
}
int main()
{
	int T,i;
	ll a,b;
	scanf("%d",&T);
	for(jc[0]=jcc[0]=1,i=1;i<mod;i++)	jc[i]=jc[i-1]*i%mod;
	while(T--)
	{
		scanf("%lld%lld%lld",&n,&a,&b);
		printf("%lld\n",(dfs(n+b-a+1,n)+mod-1)%mod);
	}
	return 0;
}