数据结构和算法(Golang实现)(25)排序算法-快速排序
快速排序
快速排序是一种分治策略的排序算法,是由英国计算机科学家Tony Hoare发明的, 该算法被发布在1961年的Communications of the ACM 国际计算机学会月刊。
注:ACM = Association for Computing Machinery,国际计算机学会,世界性的计算机从业员专业组织,创立于1947年,是世界上第一个科学性及教育性计算机学会。
快速排序是对冒泡排序的一种改进,也属于交换类的排序算法。
一、算法介绍
快速排序通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
步骤如下:
- 先从数列中取出一个数作为基准数。一般取第一个数。
- 分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
- 再对左右区间重复第二步,直到各区间只有一个数。
举一个例子:5 9 1 6 8 14 6 49 25 4 6 3。
一般取第一个数 5 作为基准,从它左边和最后一个数使用[]进行标志,
如果左边的数比基准数大,那么该数要往右边扔,也就是两个[]数交换,这样大于它的数就在右边了,然后右边[]数左移,否则左边[]数右移。
5 [9] 1 6 8 14 6 49 25 4 6 [3] 因为 9 > 5,两个[]交换位置后,右边[]左移
5 [3] 1 6 8 14 6 49 25 4 [6] 9 因为 3 !> 5,两个[]不需要交换,左边[]右移
5 3 [1] 6 8 14 6 49 25 4 [6] 9 因为 1 !> 5,两个[]不需要交换,左边[]右移
5 3 1 [6] 8 14 6 49 25 4 [6] 9 因为 6 > 5,两个[]交换位置后,右边[]左移
5 3 1 [6] 8 14 6 49 25 [4] 6 9 因为 6 > 5,两个[]交换位置后,右边[]左移
5 3 1 [4] 8 14 6 49 [25] 6 6 9 因为 4 !> 5,两个[]不需要交换,左边[]右移
5 3 1 4 [8] 14 6 49 [25] 6 6 9 因为 8 > 5,两个[]交换位置后,右边[]左移
5 3 1 4 [25] 14 6 [49] 8 6 6 9 因为 25 > 5,两个[]交换位置后,右边[]左移
5 3 1 4 [49] 14 [6] 25 8 6 6 9 因为 49 > 5,两个[]交换位置后,右边[]左移
5 3 1 4 [6] [14] 49 25 8 6 6 9 因为 6 > 5,两个[]交换位置后,右边[]左移
5 3 1 4 [14] 6 49 25 8 6 6 9 两个[]已经汇总,因为 14 > 5,所以 5 和[]之前的数 4 交换位置
第一轮切分结果:4 3 1 5 14 6 49 25 8 6 6 9
现在第一轮快速排序已经将数列分成两个部分:
4 3 1 和 14 6 49 25 8 6 6 9
左边的数列都小于 5,右边的数列都大于 5。
使用递归分别对两个数列进行快速排序。
快速排序主要靠基准数进行切分,将数列分成两部分,一部分比基准数都小,一部分比基准数都大。
在最好情况下,每一轮都能平均切分,这样遍历元素只要n/2次就可以把数列分成两部分,每一轮的时间复杂度都是:O(n)。因为问题规模每次被折半,折半的数列继续递归进行切分,也就是总的时间复杂度计算公式为:T(n) = 2*T(n/2) + O(n)。按照主定理公式计算,我们可以知道时间复杂度为:O(nlogn),当然我们可以来具体计算一下:
我们来分析最好情况,每次切分遍历元素的次数为 n/2
T(n) = 2*T(n/2) + n/2
T(n/2) = 2*T(n/4) + n/4
T(n/4) = 2*T(n/8) + n/8
T(n/8) = 2*T(n/16) + n/16
...
T(4) = 2*T(2) + 4
T(2) = 2*T(1) + 2
T(1) = 1
进行合并也就是:
T(n) = 2*T(n/2) + n/2
= 2^2*T(n/4)+ n/2 + n/2
= 2^3*T(n/8) + n/2 + n/2 + n/2
= 2^4*T(n/16) + n/2 + n/2 + n/2 + n/2
= ...
= 2^logn*T(1) + logn * n/2
= 2^logn + 1/2*nlogn
= n + 1/2*nlogn
因为当问题规模 n 趋于无穷大时 nlogn 比 n 大,所以 T(n) = O(nlogn)。
最好时间复杂度为:O(nlogn)。
最差的情况下,每次都不能平均地切分,每次切分都因为基准数是最大的或者最小的,不能分成两个数列,这样时间复杂度变为了T(n) = T(n-1) + O(n),按照主定理计算可以知道时间复杂度为:O(n^2),我们可以来实际计算一下:
我们来分析最差情况,每次切分遍历元素的次数为 n
T(n) = T(n-1) + n
= T(n-2) + n-1 + n
= T(n-3) + n-2 + n-1 + n
= ...
= T(1) + 2 +3 + ... + n-2 + n-1 + n
= O(n^2)
最差时间复杂度为:O(n^2)。
根据熵的概念,数量越大,随机性越高,越自发无序,所以待排序数据规模非常大时,出现最差情况的情形较少。在综合情况下,快速排序的平均时间复杂度为:O(nlogn)。对比之前介绍的排序算法,快速排序比那些动不动就是平方级别的初级排序算法更佳。
切分的结果极大地影响快速排序的性能,为了避免切分不均匀情况的发生,有几种方法改进:
- 每次进行快速排序切分时,先将数列随机打乱,再进行切分,这样随机加了个震荡,减少不均匀的情况。当然,也可以随机选择一个基准数,而不是选第一个数。
- 每次取数列头部,中部,尾部三个数,取三个数的中位数为基准数进行切分。
方法 1 相对好,而方法 2 引入了额外的比较操作,一般情况下我们可以随机选择一个基准数。
快速排序使用原地排序,存储空间复杂度为:O(1)。而因为递归栈的影响,递归的程序栈开辟的层数范围在logn~n,所以递归栈的空间复杂度为:O(logn)~log(n),最坏为:log(n),当元素较多时,程序栈可能溢出。通过改进算法,使用伪尾递归进行优化,递归栈的空间复杂度可以减小到O(logn),可以见下面算法优化。
快速排序是不稳定的,因为切分过程中进行了交换,相同值的元素可能发生位置变化。
二、算法实现
package main
import "fmt"
// 普通快速排序
func QuickSort(array []int, begin, end int) {
if begin < end {
// 进行切分
loc := partition(array, begin, end)
// 对左部分进行快排
QuickSort(array, begin, loc-1)
// 对右部分进行快排
QuickSort(array, loc+1, end)
}
}
// 切分函数,并返回切分元素的下标
func partition(array []int, begin, end int) int {
i := begin + 1 // 将array[begin]作为基准数,因此从array[begin+1]开始与基准数比较!
j := end // array[end]是数组的最后一位
// 没重合之前
for i < j {
if array[i] > array[begin] {
array[i], array[j] = array[j], array[i] // 交换
j--
} else {
i++
}
}
/* 跳出while循环后,i = j。
* 此时数组被分割成两个部分 --> array[begin+1] ~ array[i-1] < array[begin]
* --> array[i+1] ~ array[end] > array[begin]
* 这个时候将数组array分成两个部分,再将array[i]与array[begin]进行比较,决定array[i]的位置。
* 最后将array[i]与array[begin]交换,进行两个分割部分的排序!以此类推,直到最后i = j不满足条件就退出!
*/
if array[i] >= array[begin] { // 这里必须要取等“>=”,否则数组元素由相同的值组成时,会出现错误!
i--
}
array[begin], array[i] = array[i], array[begin]
return i
}
func main() {
list := []int{5}
QuickSort(list, 0, len(list)-1)
fmt.Println(list)
list1 := []int{5, 9}
QuickSort(list1, 0, len(list1)-1)
fmt.Println(list1)
list2 := []int{5, 9, 1}
QuickSort(list2, 0, len(list2)-1)
fmt.Println(list2)
list3 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
QuickSort(list3, 0, len(list3)-1)
fmt.Println(list3)
}
输出:
[5]
[5 9]
[1 5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]
示例图:
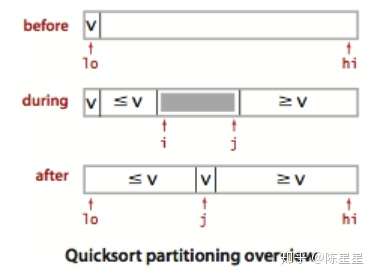
快速排序,每一次切分都维护两个下标,进行推进,最后将数列分成两部分。
三、算法改进
快速排序可以继续进行算法改进。
- 在小规模数组的情况下,直接插入排序的效率最好,当快速排序递归部分进入小数组范围,可以切换成直接插入排序。
- 排序数列可能存在大量重复值,使用三向切分快速排序,将数组分成三部分,大于基准数,等于基准数,小于基准数,这个时候需要维护三个下标。
- 使用伪尾递归减少程序栈空间占用,使得栈空间复杂度从
O(logn)~log(n)变为:O(logn)。
3.1 改进:小规模数组使用直接插入排序
func QuickSort1(array []int, begin, end int) {
if begin < end {
// 当数组小于 4 时使用直接插入排序
if end-begin <= 4 {
InsertSort(array[begin : end+1])
return
}
// 进行切分
loc := partition(array, begin, end)
// 对左部分进行快排
QuickSort1(array, begin, loc-1)
// 对右部分进行快排
QuickSort1(array, loc+1, end)
}
}
直接插入排序在小规模数组下效率极好,我们只需将end-begin <= 4的递归部分换成直接插入排序,这部分表示小数组排序。
3.2 改进:三向切分
package main
import "fmt"
// 三切分的快速排序
func QuickSort2(array []int, begin, end int) {
if begin < end {
// 三向切分函数,返回左边和右边下标
lt, gt := partition3(array, begin, end)
// 从lt到gt的部分是三切分的中间数列
// 左边三向快排
QuickSort2(array, begin, lt-1)
// 右边三向快排
QuickSort2(array, gt+1, end)
}
}
// 切分函数,并返回切分元素的下标
func partition3(array []int, begin, end int) (int, int) {
lt := begin // 左下标从第一位开始
gt := end // 右下标是数组的最后一位
i := begin + 1 // 中间下标,从第二位开始
v := array[begin] // 基准数
// 以中间坐标为准
for i <= gt {
if array[i] > v { // 大于基准数,那么交换,右指针左移
array[i], array[gt] = array[gt], array[i]
gt--
} else if array[i] < v { // 小于基准数,那么交换,左指针右移
array[i], array[lt] = array[lt], array[i]
lt++
i++
} else {
i++
}
}
return lt, gt
}
演示:
数列:4 8 2 4 4 4 7 9,基准数为 4
[4] [8] 2 4 4 4 7 [9] 从中间[]开始:8 > 4,中右[]进行交换,右边[]左移
[4] [9] 2 4 4 4 [7] 8 从中间[]开始:9 > 4,中右[]进行交换,右边[]左移
[4] [7] 2 4 4 [4] 9 8 从中间[]开始:7 > 4,中右[]进行交换,右边[]左移
[4] [4] 2 4 [4] 7 9 8 从中间[]开始:4 == 4,不需要交换,中间[]右移
[4] 4 [2] 4 [4] 7 9 8 从中间[]开始:2 < 4,中左[]需要交换,中间和左边[]右移
2 [4] 4 [4] [4] 7 9 8 从中间[]开始:4 == 4,不需要交换,中间[]右移
2 [4] 4 4 [[4]] 7 9 8 从中间[]开始:4 == 4,不需要交换,中间[]右移,因为已经重叠了
第一轮结果:2 4 4 4 4 7 9 8
分成三个数列:
2
4 4 4 4 (元素相同的会聚集在中间数列)
7 9 8
接着对第一个和最后一个数列进行递归即可。
示例图:
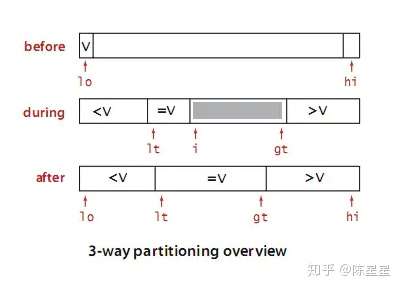
三切分,把小于基准数的扔到左边,大于基准数的扔到右边,相同的元素会进行聚集。
如果存在大量重复元素,排序速度将极大提高,将会是线性时间,因为相同的元素将会聚集在中间,这些元素不再进入下一个递归迭代。
三向切分主要来自荷兰国旗三色问题,该问题由Dijkstra提出。

假设有一条绳子,上面有红、白、蓝三种颜色的旗子,起初绳子上的旗子颜色并没有顺序,您希望将之分类,并排列为蓝、白、红的顺序,要如何移动次数才会最少,注意您只能在绳子上进行这个动作,而且一次只能调换两个旗子。
可以看到,上面的解答相当于使用三向切分一次,只要我们将白色旗子的值设置为100,蓝色的旗子值设置为0,红色旗子值设置为200,以100作为基准数,第一次三向切分后三种颜色的旗就排好了,因为蓝(0)白(100)红(200)。
注:艾兹格·W·迪科斯彻(Edsger Wybe Dijkstra,1930年5月11日~2002年8月6日),荷兰人,计算机科学家,曾获图灵奖。
3.3 改进:伪尾递归优化
// 伪尾递归快速排序
func QuickSort3(array []int, begin, end int) {
for begin < end {
// 进行切分
loc := partition(array, begin, end)
// 那边元素少先排哪边
if loc-begin < end-loc {
// 先排左边
QuickSort3(array, begin, loc-1)
begin = loc + 1
} else {
// 先排右边
QuickSort3(array, loc+1, end)
end = loc - 1
}
}
}
很多人以为这样子是尾递归。其实这样的快排写法是伪装的尾递归,不是真正的尾递归,因为有for循环,不是直接return QuickSort,递归还是不断地压栈,栈的层次仍然不断地增长。
但是,因为先让规模小的部分排序,栈的深度大大减少,程序栈最深不会超过logn层,这样堆栈最坏空间复杂度从O(n)降为O(logn)。
这种优化也是一种很好的优化,因为栈的层数减少了,对于排序十亿个整数,也只要:log(100 0000 0000)=29.897,占用的堆栈层数最多30层,比不进行优化,可能出现的O(n)常数层好很多。
四、补充:非递归写法
非递归写法仅仅是将之前的递归栈转化为自己维持的手工栈。
// 非递归快速排序
func QuickSort5(array []int) {
// 人工栈
helpStack := new(LinkStack)
// 第一次初始化栈,推入下标0,len(array)-1,表示第一次对全数组范围切分
helpStack.Push(len(array) - 1)
helpStack.Push(0)
// 栈非空证明存在未排序的部分
for !helpStack.IsEmpty() {
// 出栈,对begin-end范围进行切分排序
begin := helpStack.Pop() // 范围区间左边
end := helpStack.Pop() // 范围
// 进行切分
loc := partition(array, begin, end)
// 右边范围入栈
if loc+1 < end {
helpStack.Push(end)
helpStack.Push(loc + 1)
}
// 左边返回入栈
if begin < loc-1 {
helpStack.Push(loc - 1)
helpStack.Push(begin)
}
}
}
本来需要进行递归的数组范围begin,end,不使用递归,依次推入自己的人工栈,然后循环对人工栈进行处理。
我们可以看到没有递归,程序栈空间复杂度变为了:O(1),但额外的存储空间产生了。
辅助人工栈结构helpStack占用了额外的空间,存储空间由原地排序的O(1)变成了O(logn)~log(n)。
我们可以参考上面的伪尾递归版本,继续优化非递归版本,先让短一点的范围入栈,这样存储复杂度可以变为:O(logn)。如:
// 非递归快速排序优化
func QuickSort6(array []int) {
// 人工栈
helpStack := new(LinkStack)
// 第一次初始化栈,推入下标0,len(array)-1,表示第一次对全数组范围切分
helpStack.Push(len(array) - 1)
helpStack.Push(0)
// 栈非空证明存在未排序的部分
for !helpStack.IsEmpty() {
// 出栈,对begin-end范围进行切分排序
begin := helpStack.Pop() // 范围区间左边
end := helpStack.Pop() // 范围
// 进行切分
loc := partition(array, begin, end)
// 切分后右边范围大小
rSize := -1
// 切分后左边范围大小
lSize := -1
// 右边范围入栈
if loc+1 < end {
rSize = end - (loc + 1)
}
// 左边返回入栈
if begin < loc-1 {
lSize = loc - 1 - begin
}
// 两个范围,让范围小的先入栈,减少人工栈空间
if rSize != -1 && lSize != -1 {
if lSize > rSize {
helpStack.Push(end)
helpStack.Push(loc + 1)
helpStack.Push(loc - 1)
helpStack.Push(begin)
} else {
helpStack.Push(loc - 1)
helpStack.Push(begin)
helpStack.Push(end)
helpStack.Push(loc + 1)
}
} else {
if rSize != -1 {
helpStack.Push(end)
helpStack.Push(loc + 1)
}
if lSize != -1 {
helpStack.Push(loc - 1)
helpStack.Push(begin)
}
}
}
}
完整的程序如下:
package main
import (
"fmt"
"sync"
)
// 链表栈,后进先出
type LinkStack struct {
root *LinkNode // 链表起点
size int // 栈的元素数量
lock sync.Mutex // 为了并发安全使用的锁
}
// 链表节点
type LinkNode struct {
Next *LinkNode
Value int
}
// 入栈
func (stack *LinkStack) Push(v int) {
stack.lock.Lock()
defer stack.lock.Unlock()
// 如果栈顶为空,那么增加节点
if stack.root == nil {
stack.root = new(LinkNode)
stack.root.Value = v
} else {
// 否则新元素插入链表的头部
// 原来的链表
preNode := stack.root
// 新节点
newNode := new(LinkNode)
newNode.Value = v
// 原来的链表链接到新元素后面
newNode.Next = preNode
// 将新节点放在头部
stack.root = newNode
}
// 栈中元素数量+1
stack.size = stack.size + 1
}
// 出栈
func (stack *LinkStack) Pop() int {
stack.lock.Lock()
defer stack.lock.Unlock()
// 栈中元素已空
if stack.size == 0 {
panic("empty")
}
// 顶部元素要出栈
topNode := stack.root
v := topNode.Value
// 将顶部元素的后继链接链上
stack.root = topNode.Next
// 栈中元素数量-1
stack.size = stack.size - 1
return v
}
// 栈是否为空
func (stack *LinkStack) IsEmpty() bool {
return stack.size == 0
}
// 非递归快速排序
func QuickSort5(array []int) {
// 人工栈
helpStack := new(LinkStack)
// 第一次初始化栈,推入下标0,len(array)-1,表示第一次对全数组范围切分
helpStack.Push(len(array) - 1)
helpStack.Push(0)
// 栈非空证明存在未排序的部分
for !helpStack.IsEmpty() {
// 出栈,对begin-end范围进行切分排序
begin := helpStack.Pop() // 范围区间左边
end := helpStack.Pop() // 范围
// 进行切分
loc := partition(array, begin, end)
// 右边范围入栈
if loc+1 < end {
helpStack.Push(end)
helpStack.Push(loc + 1)
}
// 左边返回入栈
if begin < loc-1 {
helpStack.Push(loc - 1)
helpStack.Push(begin)
}
}
}
// 非递归快速排序优化
func QuickSort6(array []int) {
// 人工栈
helpStack := new(LinkStack)
// 第一次初始化栈,推入下标0,len(array)-1,表示第一次对全数组范围切分
helpStack.Push(len(array) - 1)
helpStack.Push(0)
// 栈非空证明存在未排序的部分
for !helpStack.IsEmpty() {
// 出栈,对begin-end范围进行切分排序
begin := helpStack.Pop() // 范围区间左边
end := helpStack.Pop() // 范围
// 进行切分
loc := partition(array, begin, end)
// 切分后右边范围大小
rSize := -1
// 切分后左边范围大小
lSize := -1
// 右边范围入栈
if loc+1 < end {
rSize = end - (loc + 1)
}
// 左边返回入栈
if begin < loc-1 {
lSize = loc - 1 - begin
}
// 两个范围,让范围小的先入栈,减少人工栈空间
if rSize != -1 && lSize != -1 {
if lSize > rSize {
helpStack.Push(end)
helpStack.Push(loc + 1)
helpStack.Push(loc - 1)
helpStack.Push(begin)
} else {
helpStack.Push(loc - 1)
helpStack.Push(begin)
helpStack.Push(end)
helpStack.Push(loc + 1)
}
} else {
if rSize != -1 {
helpStack.Push(end)
helpStack.Push(loc + 1)
}
if lSize != -1 {
helpStack.Push(loc - 1)
helpStack.Push(begin)
}
}
}
}
// 切分函数,并返回切分元素的下标
func partition(array []int, begin, end int) int {
i := begin + 1 // 将array[begin]作为基准数,因此从array[begin+1]开始与基准数比较!
j := end // array[end]是数组的最后一位
// 没重合之前
for i < j {
if array[i] > array[begin] {
array[i], array[j] = array[j], array[i] // 交换
j--
} else {
i++
}
}
/* 跳出while循环后,i = j。
* 此时数组被分割成两个部分 --> array[begin+1] ~ array[i-1] < array[begin]
* --> array[i+1] ~ array[end] > array[begin]
* 这个时候将数组array分成两个部分,再将array[i]与array[begin]进行比较,决定array[i]的位置。
* 最后将array[i]与array[begin]交换,进行两个分割部分的排序!以此类推,直到最后i = j不满足条件就退出!
*/
if array[i] >= array[begin] { // 这里必须要取等“>=”,否则数组元素由相同的值组成时,会出现错误!
i--
}
array[begin], array[i] = array[i], array[begin]
return i
}
func main() {
list3 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
QuickSort5(list3)
fmt.Println(list3)
list4 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
QuickSort6(list4)
fmt.Println(list4)
}
输出:
[1 3 4 5 6 6 6 8 9 14 25 49]
[1 3 4 5 6 6 6 8 9 14 25 49]
使用人工栈替代递归的程序栈,换汤不换药,速度并没有什么变化,但是代码可读性降低。
五、补充:内置库使用快速排序的原因
首先堆排序,归并排序最好最坏时间复杂度都是:O(nlogn),而快速排序最坏的时间复杂度是:O(n^2),但是很多编程语言内置的排序算法使用的仍然是快速排序,这是为什么?
- 这个问题有偏颇,选择排序算法要看具体的场景,
Linux内核用的排序算法就是堆排序,而Java对于数量比较多的复杂对象排序,内置排序使用的是归并排序,只是一般情况下,快速排序更快。 - 归并排序有两个稳定,第一个稳定是排序前后相同的元素位置不变,第二个稳定是,每次都是很平均地进行排序,读取数据也是顺序读取,能够利用存储器缓存的特征,比如从磁盘读取数据进行排序。因为排序过程需要占用额外的辅助数组空间,所以这部分有代价损耗,但是原地手摇的归并排序克服了这个缺陷。
- 复杂度中,大
O有一个常数项被省略了,堆排序每次取最大的值之后,都需要进行节点翻转,重新恢复堆的特征,做了大量无用功,常数项比快速排序大,大部分情况下比快速排序慢很多。但是堆排序时间较稳定,不会出现快排最坏O(n^2)的情况,且省空间,不需要额外的存储空间和栈空间。 - 当待排序数量大于16000个元素时,使用自底向上的堆排序比快速排序还快,可见此:https://core.ac.uk/download/pdf/82350265.pdf。
- 快速排序最坏情况下复杂度高,主要在于切分不像归并排序一样平均,而是很依赖基准数的现在,我们通过改进,比如随机数,三切分等,这种最坏情况的概率极大的降低。大多数情况下,它并不会那么地坏,大多数快才是真的块。
- 归并排序和快速排序都是分治法,排序的数据都是相邻的,而堆排序比较的数可能跨越很大的范围,导致局部性命中率降低,不能利用现代存储器缓存的特征,加载数据过程会损失性能。
对稳定性有要求的,要求排序前后相同元素位置不变,可以使用归并排序,Java中的复杂对象类型,要求排序前后位置不能发生变化,所以小规模数据下使用了直接插入排序,大规模数据下使用了归并排序。
对栈,存储空间有要求的可以使用堆排序,比如Linux内核栈小,快速排序占用程序栈太大了,使用快速排序可能栈溢出,所以使用了堆排序。
在Golang中,标准库sort中对切片进行稳定排序:
func SliceStable(slice interface{}, less func(i, j int) bool) {
rv := reflectValueOf(slice)
swap := reflectSwapper(slice)
stable_func(lessSwap{less, swap}, rv.Len())
}
func stable_func(data lessSwap, n int) {
blockSize := 20
a, b := 0, blockSize
for b <= n {
insertionSort_func(data, a, b)
a = b
b += blockSize
}
insertionSort_func(data, a, n)
for blockSize < n {
a, b = 0, 2*blockSize
for b <= n {
symMerge_func(data, a, a+blockSize, b)
a = b
b += 2 * blockSize
}
if m := a + blockSize; m < n {
symMerge_func(data, a, m, n)
}
blockSize *= 2
}
}
会先按照20个元素的范围,对整个切片分段进行插入排序,因为小数组插入排序效率高,然后再对这些已排好序的小数组进行归并排序。其中归并排序还使用了原地排序,节约了辅助空间。
而一般的排序:
func Slice(slice interface{}, less func(i, j int) bool) {
rv := reflectValueOf(slice)
swap := reflectSwapper(slice)
length := rv.Len()
quickSort_func(lessSwap{less, swap}, 0, length, maxDepth(length))
}
func quickSort_func(data lessSwap, a, b, maxDepth int) {
for b-a > 12 {
if maxDepth == 0 {
heapSort_func(data, a, b)
return
}
maxDepth--
mlo, mhi := doPivot_func(data, a, b)
if mlo-a < b-mhi {
quickSort_func(data, a, mlo, maxDepth)
a = mhi
} else {
quickSort_func(data, mhi, b, maxDepth)
b = mlo
}
}
if b-a > 1 {
for i := a + 6; i < b; i++ {
if data.Less(i, i-6) {
data.Swap(i, i-6)
}
}
insertionSort_func(data, a, b)
}
}
func doPivot_func(data lessSwap, lo, hi int) (midlo, midhi int) {
m := int(uint(lo+hi) >> 1)
if hi-lo > 40 {
s := (hi - lo) / 8
medianOfThree_func(data, lo, lo+s, lo+2*s)
medianOfThree_func(data, m, m-s, m+s)
medianOfThree_func(data, hi-1, hi-1-s, hi-1-2*s)
}
medianOfThree_func(data, lo, m, hi-1)
pivot := lo
a, c := lo+1, hi-1
for ; a < c && data.Less(a, pivot); a++ {
}
b := a
for {
for ; b < c && !data.Less(pivot, b); b++ {
}
for ; b < c && data.Less(pivot, c-1); c-- {
}
if b >= c {
break
}
data.Swap(b, c-1)
b++
c--
}
protect := hi-c < 5
if !protect && hi-c < (hi-lo)/4 {
dups := 0
if !data.Less(pivot, hi-1) {
data.Swap(c, hi-1)
c++
dups++
}
if !data.Less(b-1, pivot) {
b--
dups++
}
if !data.Less(m, pivot) {
data.Swap(m, b-1)
b--
dups++
}
protect = dups > 1
}
if protect {
for {
for ; a < b && !data.Less(b-1, pivot); b-- {
}
for ; a < b && data.Less(a, pivot); a++ {
}
if a >= b {
break
}
data.Swap(a, b-1)
a++
b--
}
}
data.Swap(pivot, b-1)
return b - 1, c
}
快速排序限制程序栈的层数为:2*ceil(log(n+1)),当递归超过该层时表示程序栈过深,那么转为堆排序。
上述快速排序还使用了三种优化,第一种是递归时小数组转为插入排序,第二种是使用了中位数基准数,第三种使用了三切分。
系列文章入口
我是陈星星,欢迎阅读我亲自写的 数据结构和算法(Golang实现),文章首发于 阅读更友好的GitBook。
- 数据结构和算法(Golang实现)(1)简单入门Golang-前言
- 数据结构和算法(Golang实现)(2)简单入门Golang-包、变量和函数
- 数据结构和算法(Golang实现)(3)简单入门Golang-流程控制语句
- 数据结构和算法(Golang实现)(4)简单入门Golang-结构体和方法
- 数据结构和算法(Golang实现)(5)简单入门Golang-接口
- 数据结构和算法(Golang实现)(6)简单入门Golang-并发、协程和信道
- 数据结构和算法(Golang实现)(7)简单入门Golang-标准库
- 数据结构和算法(Golang实现)(8.1)基础知识-前言
- 数据结构和算法(Golang实现)(8.2)基础知识-分治法和递归
- 数据结构和算法(Golang实现)(9)基础知识-算法复杂度及渐进符号
- 数据结构和算法(Golang实现)(10)基础知识-算法复杂度主方法
- 数据结构和算法(Golang实现)(11)常见数据结构-前言
- 数据结构和算法(Golang实现)(12)常见数据结构-链表
- 数据结构和算法(Golang实现)(13)常见数据结构-可变长数组
- 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
- 数据结构和算法(Golang实现)(15)常见数据结构-列表
- 数据结构和算法(Golang实现)(16)常见数据结构-字典
- 数据结构和算法(Golang实现)(17)常见数据结构-树
- 数据结构和算法(Golang实现)(18)排序算法-前言
- 数据结构和算法(Golang实现)(19)排序算法-冒泡排序
- 数据结构和算法(Golang实现)(20)排序算法-选择排序
- 数据结构和算法(Golang实现)(21)排序算法-插入排序
- 数据结构和算法(Golang实现)(22)排序算法-希尔排序
- 数据结构和算法(Golang实现)(23)排序算法-归并排序
- 数据结构和算法(Golang实现)(24)排序算法-优先队列及堆排序
- 数据结构和算法(Golang实现)(25)排序算法-快速排序
- 数据结构和算法(Golang实现)(26)查找算法-哈希表
- 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
- 数据结构和算法(Golang实现)(28)查找算法-AVL树
- 数据结构和算法(Golang实现)(29)查找算法-2-3树和左倾红黑树
- 数据结构和算法(Golang实现)(30)查找算法-2-3-4树和普通红黑树
数据结构和算法(Golang实现)(25)排序算法-快速排序的更多相关文章
- 数据结构和算法(Golang实现)(18)排序算法-前言
排序算法 人类的发展中,我们学会了计数,比如知道小明今天打猎的兔子的数量是多少.另外一方面,我们也需要判断,今天哪个人打猎打得多,我们需要比较. 所以,排序这个很自然的需求就出来了.比如小明打了5只兔 ...
- 数据结构和算法(Golang实现)(19)排序算法-冒泡排序
冒泡排序 冒泡排序是大多数人学的第一种排序算法,在面试中,也是问的最多的一种,有时候还要求手写排序代码,因为比较简单. 冒泡排序属于交换类的排序算法. 一.算法介绍 现在有一堆乱序的数,比如:5 9 ...
- 数据结构和算法(Golang实现)(20)排序算法-选择排序
选择排序 选择排序,一般我们指的是简单选择排序,也可以叫直接选择排序,它不像冒泡排序一样相邻地交换元素,而是通过选择最小的元素,每轮迭代只需交换一次.虽然交换次数比冒泡少很多,但效率和冒泡排序一样的糟 ...
- 数据结构和算法(Golang实现)(21)排序算法-插入排序
插入排序 插入排序,一般我们指的是简单插入排序,也可以叫直接插入排序.就是说,每次把一个数插到已经排好序的数列里面形成新的排好序的数列,以此反复. 插入排序属于插入类排序算法. 除了我以外,有些人打扑 ...
- 数据结构和算法(Golang实现)(22)排序算法-希尔排序
希尔排序 1959 年一个叫Donald L. Shell (March 1, 1924 – November 2, 2015)的美国人在Communications of the ACM 国际计算机 ...
- 数据结构和算法(Golang实现)(23)排序算法-归并排序
归并排序 归并排序是一种分治策略的排序算法.它是一种比较特殊的排序算法,通过递归地先使每个子序列有序,再将两个有序的序列进行合并成一个有序的序列. 归并排序首先由著名的现代计算机之父John_von_ ...
- 数据结构和算法(Golang实现)(24)排序算法-优先队列及堆排序
优先队列及堆排序 堆排序(Heap Sort)由威尔士-加拿大计算机科学家J. W. J. Williams在1964年发明,它利用了二叉堆(A binary heap)的性质实现了排序,并证明了二叉 ...
- 数据结构和算法(Golang实现)(26)查找算法-哈希表
哈希表:散列查找 一.线性查找 我们要通过一个键key来查找相应的值value.有一种最简单的方式,就是将键值对存放在链表里,然后遍历链表来查找是否存在key,存在则更新键对应的值,不存在则将键值对链 ...
- 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
二叉查找树 二叉查找树,又叫二叉排序树,二叉搜索树,是一种有特定规则的二叉树,定义如下: 它是一颗二叉树,或者是空树. 左子树所有节点的值都小于它的根节点,右子树所有节点的值都大于它的根节点. 左右子 ...
随机推荐
- LeetCode#232-Implement Queue using Stacks-用栈实现队列
一.题目 使用栈实现队列的下列操作: push(x) -- 将一个元素放入队列的尾部. pop() -- 从队列首部移除元素. peek() -- 返回队列首部的元素. empty() -- 返回队列 ...
- STL篇--list容器
list容器: 1.list 容器 的本质就是双向环形链表,最后一个节点刻意做成空节点,符合容器的左闭右开的原则2.list 的迭代器 是一个智能指针,其实就是一个类,通过操作符重载模拟各种操作(++ ...
- JavaScript 模式》读书笔记(4)— 函数2
这篇,我们仍旧继续学习函数. 二.回调模式 函数都是对象,这表示它们可以作为参数传递给其它函数. function writeCode(callback) { // 执行一些事务... callbac ...
- Ansible权威指南-读书笔记
2 Ansible基础元素介绍 2.1 ansible 目录结构介绍 2.2 ansible 配置文件解析 配置文件解析顺序:当前命令执行目录-->用户家目录下的.ansible.cfg--&g ...
- 洛谷1265prim算法求最小生成树
题目链接:https://www.luogu.com.cn/problem/P1265 最小生成树的prim算法跟dijkstra算法非常像,就是将点分成两个集合,一个是已经在生成树中的点的集合,一个 ...
- java实现SSO(SingleSignOn)单点登录服务
单点登录SSO:是指用户通过一次登录,可以访问任意所有相互信任的应用系统.即一处登录,处处登录.比如阿里系下的淘宝.天猫等,虽然是不同的产品,但归于一个体系下,是可以相互信任的应用系统. 为了方便用户 ...
- vue基础指令学习
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- 4D
GIS行业通常将GIS常用的数据产品概括为“4D”,即:DOM(数字正射影像图).DEM(数字高程模型).DLG(数字线划地图).DRG(数字栅格地图).以及复合模式派生数据组成. DOM:数字正射影 ...
- 数塔(杭电oj2084)
Problem Description 在讲述DP算法的时候,一个经典的例子就是数塔问题,它是这样描述的: 有如下所示的数塔,要求从顶层走到底层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大 ...
- spring中BeanPostProcessor之一:InstantiationAwareBeanPostProcessor(01)
在spring中beanPostProcessor绝对是开天辟地的产物,给了程序员很多自主权,beanPostProcessor即常说的bean后置处理器. 一.概览 先来说下Instantiatio ...
