【python实现卷积神经网络】优化器的实现（SGD、Nesterov、Adagrad、Adadelta、RMSprop、Adam）

代码来源：https://github.com/eriklindernoren/ML-From-Scratch

卷积神经网络中卷积层Conv2D（带stride、padding）的具体实现：https://www.cnblogs.com/xiximayou/p/12706576.html

激活函数的实现（sigmoid、softmax、tanh、relu、leakyrelu、elu、selu、softplus）：https://www.cnblogs.com/xiximayou/p/12713081.html

损失函数定义（均方误差、交叉熵损失）：https://www.cnblogs.com/xiximayou/p/12713198.html

先看下优化器实现的代码：

import numpy as np
from mlfromscratch.utils import make_diagonal, normalize

# Optimizers for models that use gradient based methods for finding the
# weights that minimizes the loss.
# A great resource for understanding these methods:
# http://sebastianruder.com/optimizing-gradient-descent/index.html

class StochasticGradientDescent():
    def __init__(self, learning_rate=0.01, momentum=0):
        self.learning_rate = learning_rate
        self.momentum = momentum
        self.w_updt = None

    def update(self, w, grad_wrt_w):
        # If not initialized
        if self.w_updt is None:
            self.w_updt = np.zeros(np.shape(w))
        # Use momentum if set
        self.w_updt = self.momentum * self.w_updt + (1 - self.momentum) * grad_wrt_w
        # Move against the gradient to minimize loss
        return w - self.learning_rate * self.w_updt

class NesterovAcceleratedGradient():
    def __init__(self, learning_rate=0.001, momentum=0.4):
        self.learning_rate = learning_rate
        self.momentum = momentum
        self.w_updt = np.array([])

    def update(self, w, grad_func):
        # Calculate the gradient of the loss a bit further down the slope from w
        approx_future_grad = np.clip(grad_func(w - self.momentum * self.w_updt), -1, 1)
        # Initialize on first update
        if not self.w_updt.any():
            self.w_updt = np.zeros(np.shape(w))

        self.w_updt = self.momentum * self.w_updt + self.learning_rate * approx_future_grad
        # Move against the gradient to minimize loss
        return w - self.w_updt

class Adagrad():
    def __init__(self, learning_rate=0.01):
        self.learning_rate = learning_rate
        self.G = None # Sum of squares of the gradients
        self.eps = 1e-8

    def update(self, w, grad_wrt_w):
        # If not initialized
        if self.G is None:
            self.G = np.zeros(np.shape(w))
        # Add the square of the gradient of the loss function at w
        self.G += np.power(grad_wrt_w, 2)
        # Adaptive gradient with higher learning rate for sparse data
        return w - self.learning_rate * grad_wrt_w / np.sqrt(self.G + self.eps)

class Adadelta():
    def __init__(self, rho=0.95, eps=1e-6):
        self.E_w_updt = None # Running average of squared parameter updates
        self.E_grad = None   # Running average of the squared gradient of w
        self.w_updt = None   # Parameter update
        self.eps = eps
        self.rho = rho

    def update(self, w, grad_wrt_w):
        # If not initialized
        if self.w_updt is None:
            self.w_updt = np.zeros(np.shape(w))
            self.E_w_updt = np.zeros(np.shape(w))
            self.E_grad = np.zeros(np.shape(grad_wrt_w))

        # Update average of gradients at w
        self.E_grad = self.rho * self.E_grad + (1 - self.rho) * np.power(grad_wrt_w, 2)

        RMS_delta_w = np.sqrt(self.E_w_updt + self.eps)
        RMS_grad = np.sqrt(self.E_grad + self.eps)

        # Adaptive learning rate
        adaptive_lr = RMS_delta_w / RMS_grad

        # Calculate the update
        self.w_updt = adaptive_lr * grad_wrt_w

        # Update the running average of w updates
        self.E_w_updt = self.rho * self.E_w_updt + (1 - self.rho) * np.power(self.w_updt, 2)

        return w - self.w_updt

class RMSprop():
    def __init__(self, learning_rate=0.01, rho=0.9):
        self.learning_rate = learning_rate
        self.Eg = None # Running average of the square gradients at w
        self.eps = 1e-8
        self.rho = rho

    def update(self, w, grad_wrt_w):
        # If not initialized
        if self.Eg is None:
            self.Eg = np.zeros(np.shape(grad_wrt_w))

        self.Eg = self.rho * self.Eg + (1 - self.rho) * np.power(grad_wrt_w, 2)

        # Divide the learning rate for a weight by a running average of the magnitudes of recent
        # gradients for that weight
        return w - self.learning_rate *  grad_wrt_w / np.sqrt(self.Eg + self.eps)

class Adam():
    def __init__(self, learning_rate=0.001, b1=0.9, b2=0.999):
        self.learning_rate = learning_rate
        self.eps = 1e-8
        self.m = None
        self.v = None
        # Decay rates
        self.b1 = b1
        self.b2 = b2

    def update(self, w, grad_wrt_w):
        # If not initialized
        if self.m is None:
            self.m = np.zeros(np.shape(grad_wrt_w))
            self.v = np.zeros(np.shape(grad_wrt_w))

        self.m = self.b1 * self.m + (1 - self.b1) * grad_wrt_w
        self.v = self.b2 * self.v + (1 - self.b2) * np.power(grad_wrt_w, 2)

        m_hat = self.m / (1 - self.b1)
        v_hat = self.v / (1 - self.b2)

        self.w_updt = self.learning_rate * m_hat / (np.sqrt(v_hat) + self.eps)

        return w - self.w_updt

这里导入了了mlfromscratch.utils中的make_diagonal, normalize函数，它们在data_manipulation.py中。但是好像没有用到，还是去看一下这两个函数：

def make_diagonal(x):
    """ Converts a vector into an diagonal matrix """
    m = np.zeros((len(x), len(x)))
    for i in range(len(m[0])):
        m[i, i] = x[i]
    return m

def normalize(X, axis=-1, order=2):
    """ Normalize the dataset X """
    l2 = np.atleast_1d(np.linalg.norm(X, order, axis))
    l2[l2 == 0] = 1
    return X / np.expand_dims(l2, axis)

make_diagonal()的作用是将x中的元素变成对角元素。

normalize()函数的作用是正则化。

补充：

• np.linalg.norm(x, ord=None, axis=None, keepdims=False)：需要注意ord的值表示的是范数的类型。
• np.atleast_1d()：改变维度，将输入直接视为1维，比如np.atleast_1d([1])的输出就是[1]
• np.expand_dims()：用于扩展数组的维度，要深入了解还是得去查一下。

然后再看看优化器的实现，以最常用的随机梯度下降为例：

class StochasticGradientDescent():
    def __init__(self, learning_rate=0.01, momentum=0):
        self.learning_rate = learning_rate
        self.momentum = momentum
        self.w_updt = None

    def update(self, w, grad_wrt_w):
        # If not initialized
        if self.w_updt is None:
            self.w_updt = np.zeros(np.shape(w))
        # Use momentum if set
        self.w_updt = self.momentum * self.w_updt + (1 - self.momentum) * grad_wrt_w
        # Move against the gradient to minimize loss
        return w - self.learning_rate * self.w_updt

直接看带动量的随机梯度下降公式：

这里的β就是动量momentum的值，一般取值是0.9。正好是对应上面的公式，最后更新W和b就是：

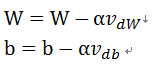
其中 α就表示学习率learning_rate。

至于不同优化器之间的优缺点就不在本文的考虑追之中了，可以自行去查下。