每日一题 - 剑指 Offer 47. 礼物的最大价值

题目信息

• 时间： 2019-07-02

• 题目链接：Leetcode

• tag：动态规划

• 难易程度：中等

• 题目描述：

  在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

注意

1. 0 < grid.length <= 200
2. 0 < grid[0].length <= 200

解题思路

本题难点

根据题目说明，某单元格可能从上边单元格或左边单元格到达。

具体思路

动态规划解决此问题，转移方程f(i,j)=max[f(i,j−1),f(i−1,j)]+grid(i,j)

设动态规划矩阵 dp(i,j) 代表从棋盘的左上角开始，到达单元格 (i,j) 时能拿到礼物的最大累计价值。

• 当 i = 0 且 j = 0时，起始元素。
• 当 i = 0 且 j != 0时，为矩阵第一行元素，只可从左边到达；
• 当 i != 0 且 j = 0时，为矩阵第一列元素，只可从上边到达；
• 当 i != 0 且 j != 0时，可从左边或上边到达；

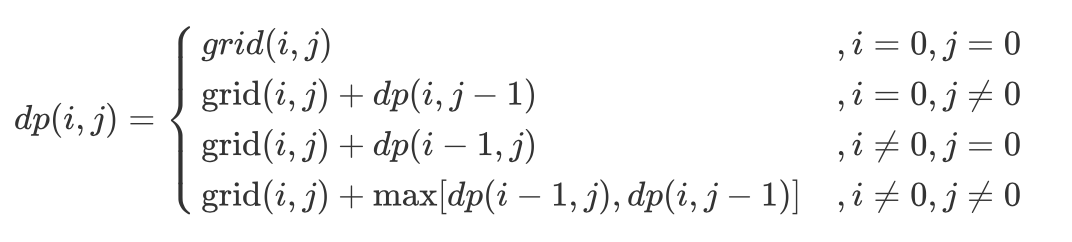
注意：由于 dp[i] [j] 只与 dp[i−1] [j] , dp[i] [j−1] , grid[ i ] [ j ]有关系，因此可以将原矩阵 grid 用作 dp 矩阵，即直接在 grid 上修改即可。

代码

class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
              // dp[0][0]=grid[0][0]
                if(i == 0 && j == 0) continue;
                if(i == 0) grid[i][j] += grid[i][j - 1] ;
                else if(j == 0) grid[i][j] += grid[i - 1][j];
                else grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);
            }
        }
      //dp[m−1][n−1] ，m,n 分别为矩阵的行高和列宽，即返回 dp 矩阵右下角元素
        return grid[m - 1][n - 1];
    }
}

复杂度分析：

• 时间复杂度 O(MN) ： M，N分别为矩阵行高、列宽；动态规划需遍历整个 grid 矩阵。
• 空间复杂度 O(1) ： 原地修改使用常数大小的额外空间。

其他优秀解答

解题思路

多开辟一个二维数组的空间，节省边界值的判断。

代码

class Solution {
    public int maxValue(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[][] dp = new int[row+1][col+1];
        for(int i = 1;i <= row;i++){
            for(int j = 1; j <= col; j++){
                dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]) + grid[i-1][j-1];
            }
        }
        return dp[row][col];
    }
}