JavaScript图形实例:递归生成树
观察自然界中树的分叉,一根主干生长出两个侧干,每个侧干又长出两个侧干,以此类推,便生长出疏密有致的结构。这样的生长结构,使用递归算法可以模拟出来。
例如,分叉的侧干按45°的偏转角度进行生长的递归示意图如图1所示。

图1 生成树的递归示意图
按照树分叉生长侧干的递归思想,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>递归分形树(一)</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="400" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var maxdepth =4;
var curdepth = 0;
var alph=Math.PI/4;
function growtree()
{
ctx.translate(300,380);
branch(-Math.PI/2);
}
function branch(angle)
{
curdepth++;
ctx.save();
ctx.strokeStyle = "green";
ctx.lineWidth = 6;
ctx.rotate(angle);
ctx.beginPath();
ctx.moveTo(0,0);
ctx.lineTo(100,0);
ctx.stroke();
ctx.translate(100,0);
ctx.scale(0.75,0.75);
if(curdepth <= maxdepth)
{
branch(alph);
branch(-alph);
}
ctx.restore();
curdepth--;
}
growtree();
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出分叉树形,如图2所示。
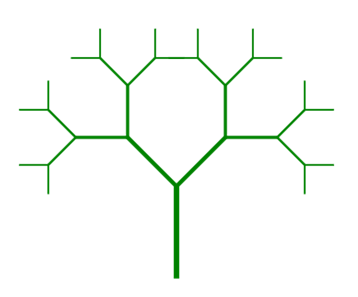
图2 递归深度maxdepth =4,alph=45°的分叉树形
若将递归深度“maxdepth=4”修改为“maxdepth=12”,则在浏览器窗口中绘制出如图3所示的分叉树形。

图3 递归深度maxdepth =12,alph=45°的分叉树形
若将递归深度“maxdepth=4”修改为“maxdepth=10”,分叉偏转角度从45°(alph=Math.PI/4)修改为30°(alph=Math.PI/6),则在浏览器窗口中绘制出如,4所示的分叉树形。
 图4 递归深度maxdepth =10,alph=30°的分叉树形
图4 递归深度maxdepth =10,alph=30°的分叉树形
由图3和图4可知,分叉的偏转角度不同,树形也会不同。实际上,自然界中树的侧干的生长不会按同一个角度进行分叉的,若将分叉的偏转角度取随机值,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>递归分形树(二)</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="400" style="border:3px double #996633;"></canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var maxdepth =10;
var curdepth = 0;
function growtree()
{
ctx.translate(300,380);
branch(-Math.PI/2);
}
function branch(angle)
{
curdepth++;
ctx.save();
ctx.strokeStyle = "green";
ctx.lineWidth = 6;
ctx.rotate(angle);
ctx.beginPath();
ctx.moveTo(0,0);
ctx.lineTo(100,0);
ctx.stroke();
ctx.translate(100,0);
ctx.scale(0.75,0.75);
if(curdepth <= maxdepth)
{
branch(randomRange(0,Math.PI/4));
branch(randomRange(-Math.PI/4,0));
}
ctx.restore();
curdepth--;
}
function randomRange(min,max)
{
return Math.random()*(max-min) + min;
}
growtree();
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,在浏览器窗口中可能会绘制出如图5所示的分叉树形。
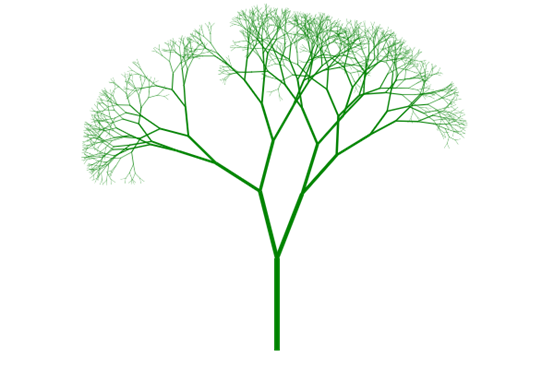
图5 分叉树形
不断地刷新浏览器窗口,可以随机绘制出不同的分叉树形,如图6所示。
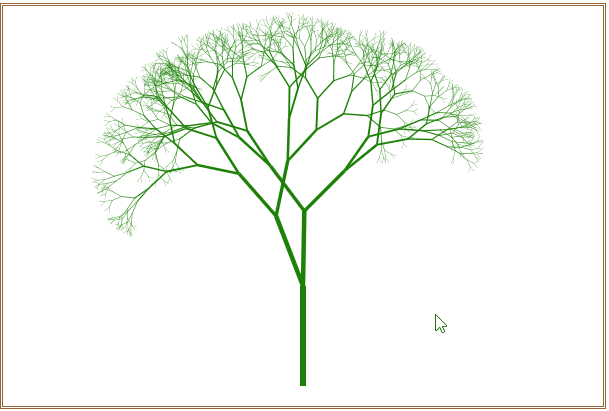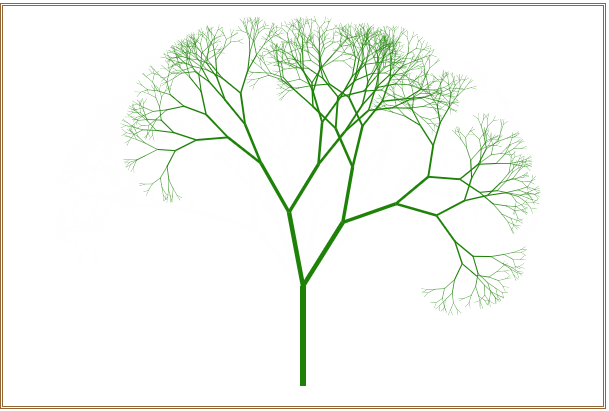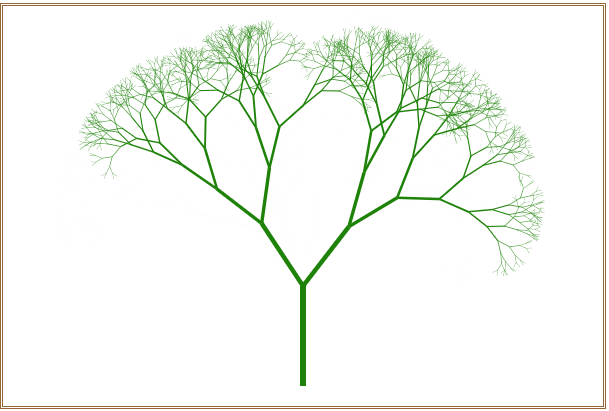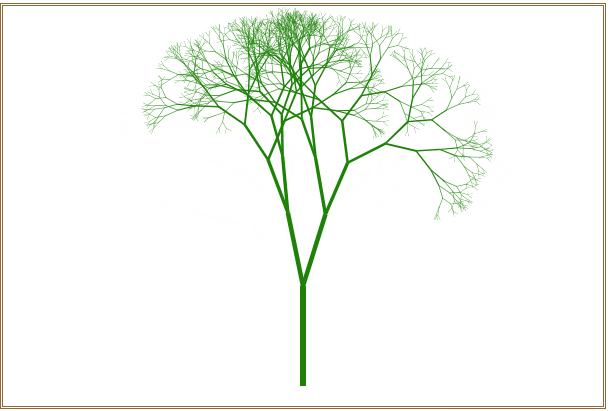
图6 绘制出的不同分叉树形
如果将递归树形的生成元改为如图7所示的三分叉,即在上面HTML文件中的两行代码
branch(randomRange(0,Math.PI/4));
branch(randomRange(-Math.PI/4,0));
中间加上一行代码 branch(0); 再将递归深度“var maxdepth =10;”修改为“var maxdepth =6;”,则在浏览器窗口中可能会绘制出如图8所示的分叉树形。

图7 三分叉生成元

图8 三分叉递归树形
我们可以在树梢画一个红色小圆,表示树儿开花了,编写如下的HTML文件。
<!DOCTYPE html>
<head>
<title>递归分形树(三)</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="400" style="border:3px double #996633;"></canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var maxdepth =10;
var curdepth = 0;
function growtree()
{
ctx.translate(300,380);
branch(-Math.PI/2);
}
function branch(angle)
{
curdepth++;
ctx.save();
ctx.strokeStyle = "green";
ctx.lineWidth = 6;
ctx.rotate(angle);
ctx.beginPath();
ctx.moveTo(0,0);
ctx.lineTo(100,0);
ctx.stroke();
ctx.translate(100,0);
ctx.scale(0.75,0.75);
if(curdepth < maxdepth)
{
branch(randomRange(0,Math.PI/4));
branch(randomRange(-Math.PI/4,0));
}
if(curdepth == maxdepth)
{
ctx.fillStyle = '#ff0000';
ctx.beginPath();
ctx.arc(0,0,20,0,Math.PI*2,true);
ctx.fill();
}
ctx.restore();
curdepth--;
}
function randomRange(min,max)
{
return Math.random()*(max-min) + min;
}
growtree();
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,在浏览器窗口中可能会绘制出如图9所示的分叉树形。

图9 树梢开红花的分叉树形
不断地刷新浏览器窗口,可以随机绘制出不同的分叉树形,如图10所示。
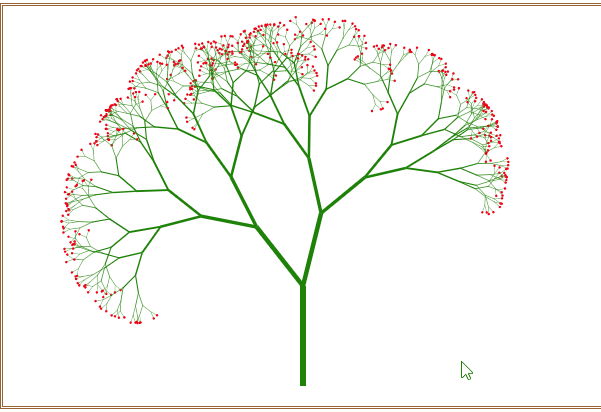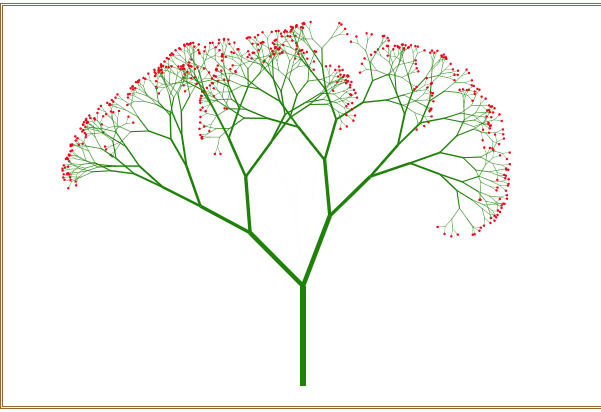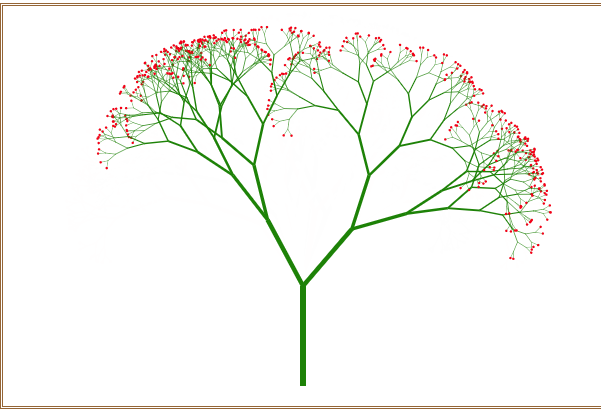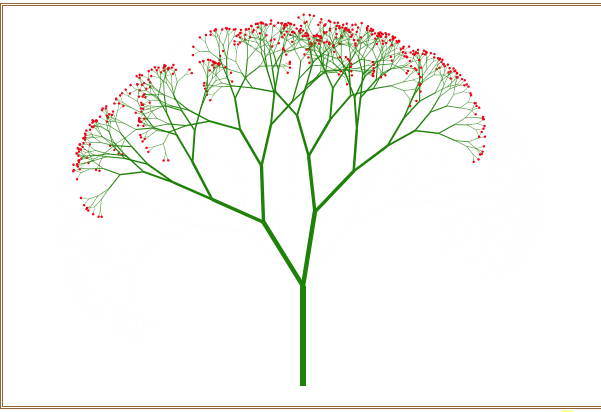
图10 绘制出的不同树梢开红花的分叉树形
JavaScript图形实例:递归生成树的更多相关文章
- JavaScript图形实例:线段构图
在“JavaScript图形实例:四瓣花型图案”和“JavaScript图形实例:蝴蝶结图案”中,我们绘制图形时,主要采用的方法是先根据给定的曲线参数方程计算出两点坐标,然后将两点用线段连接起来,线段 ...
- JavaScript图形实例:再谈IFS生成图形
在“JavaScript图形实例:迭代函数系统生成图形”一文中,我们介绍了采用迭代函数系统(Iterated Function System,IFS)创建分形图案的一些实例.在该文中,仿射变换函数W的 ...
- JavaScript图形实例:随机SierPinski三角形
在“JavaScript图形实例:SierPinski三角形”中,我们介绍了SierPinski三角形的基本绘制方法,在“JavaScript图形实例:迭代函数系统生成图形”一文中,介绍了采用IFS方 ...
- JavaScript图形实例:图形的旋转变换
旋转变换:图形上的各点绕一固定点沿圆周路径作转动称为旋转变换.可用旋转角表示旋转量的大小. 旋转变换通常约定以逆时针方向为正方向.最简单的旋转变换是以坐标原点(0,0)为旋转中心,这时,平面上一点P( ...
- JavaScript图形实例:SierPinski三角形
1.SierPinski三角形 Sierpinski三角形是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集.其生成过程为: (1)取一个三角形(多数使用等边三角形): (2) ...
- JavaScript图形实例:Hilbert曲线
德国数学家David Hilbert在1891年构造了一种曲线,首先把一个正方形等分成四个小正方形,依次从西北角的正方形中心出发往南到西南正方形中心,再往东到东南角的正方形中心,再往北到东北角正方形中 ...
- JavaScript图形实例:合成花卉图
我们知道在直角坐标系中,圆的方程可描述为: X=R*COS(α) Y=R*SIN(α) 用循环依次取α值为0~2π,计算出X和Y,在canvas画布中将坐标点(X,Y)用线连起来,可绘制出一个圆.编写 ...
- JavaScript图形实例:四瓣花型图案
设有坐标计算公式如下: X=L*(1+SIN(4α))*COS(α) Y=L*(1+SIN(4α))*SIN(α) 用循环依次取α值为0~2π,计算出X和Y,在canvas画布中对坐标位置(X,Y)描 ...
- JavaScript图形实例:图形的扇形变换和环形变换
1.1 扇形变换 将如图1所示的上边长方形的图形变换为下边的扇形图形的变换称为扇形变换. 设长方形图形中任一点P1(X1,Y1)变换为扇形图形上的点P2(X2,Y2),长方形的长为X,扇形圆心坐标为 ...
随机推荐
- Java实现 LeetCode 630 课程表 III(大小堆)
630. 课程表 III 这里有 n 门不同的在线课程,他们按从 1 到 n 编号.每一门课程有一定的持续上课时间(课程时间)t 以及关闭时间第 d 天.一门课要持续学习 t 天直到第 d 天时要完成 ...
- Java实现 LeetCode 345 反转字符串中的元音字母
345. 反转字符串中的元音字母 编写一个函数,以字符串作为输入,反转该字符串中的元音字母. 示例 1: 输入: "hello" 输出: "holle" 示例 ...
- java实现取球博弈
今盒子里有n个小球,A.B两人轮流从盒中取球,每个人都可以看到另一个人取了多少个,也可以看到盒中还剩下多少个,并且两人都很聪明,不会做出错误的判断. 我们约定: 每个人从盒子中取出的球的数目必须是:1 ...
- zabbix3.2升级3.4报错Database error
摘要: zabbix3.2版本升级到zabbix3.4版本后打开页面报错,报错内容如下 Database errorThe frontend does not match Zabbix databas ...
- 第一章03-Activity的启动模式
Activity的LaunchMode Android中提供了四中Activity的启动模式 1. standard 2. singleTop 3. singleTask 4. signleInsta ...
- const修饰this指针的用法
#include <iostream> #include <string> using namespace std; class Base { }; class Excepti ...
- webstorm 快捷键 失效问题
解决方案一: file->Settings->Keymap->设置为Default 解决方案二: file->Settings->IdeaVim->取消对勾 重 ...
- win10系统下office 2019激活
1.新建一个文本文件,创建批处理文件office.bat @echo off (cd /d "%~dp0")&&(NET FILE||(powershell sta ...
- Flutter 中由 BuildContext 引发的血案
今天和各位分享一个博主在实际开发中遇到的问题,以及解决方法.废话不多说,我们先来看需求: 我们要做一个iOS风格的底部菜单弹出组件,具体涉及showCupertinoModalPopup()方法,该方 ...
- Random Point in Triangle【随机数解决期望值问题】
Random Point in Triangle 题目链接(点击) 题目描述 Bobo has a triangle ABC with A(x1,y1),B(x2,y2)A(x1,y1),B(x2,y ...
