[一般图最大匹配]Bimatching

10566 Bimatching

• 题意：一个男生必须跟两个女生匹配，求最大匹配

• 思路：一般的二分图匹配做不了，网络流也不会建图，这题采用的是一般图匹配
  
  

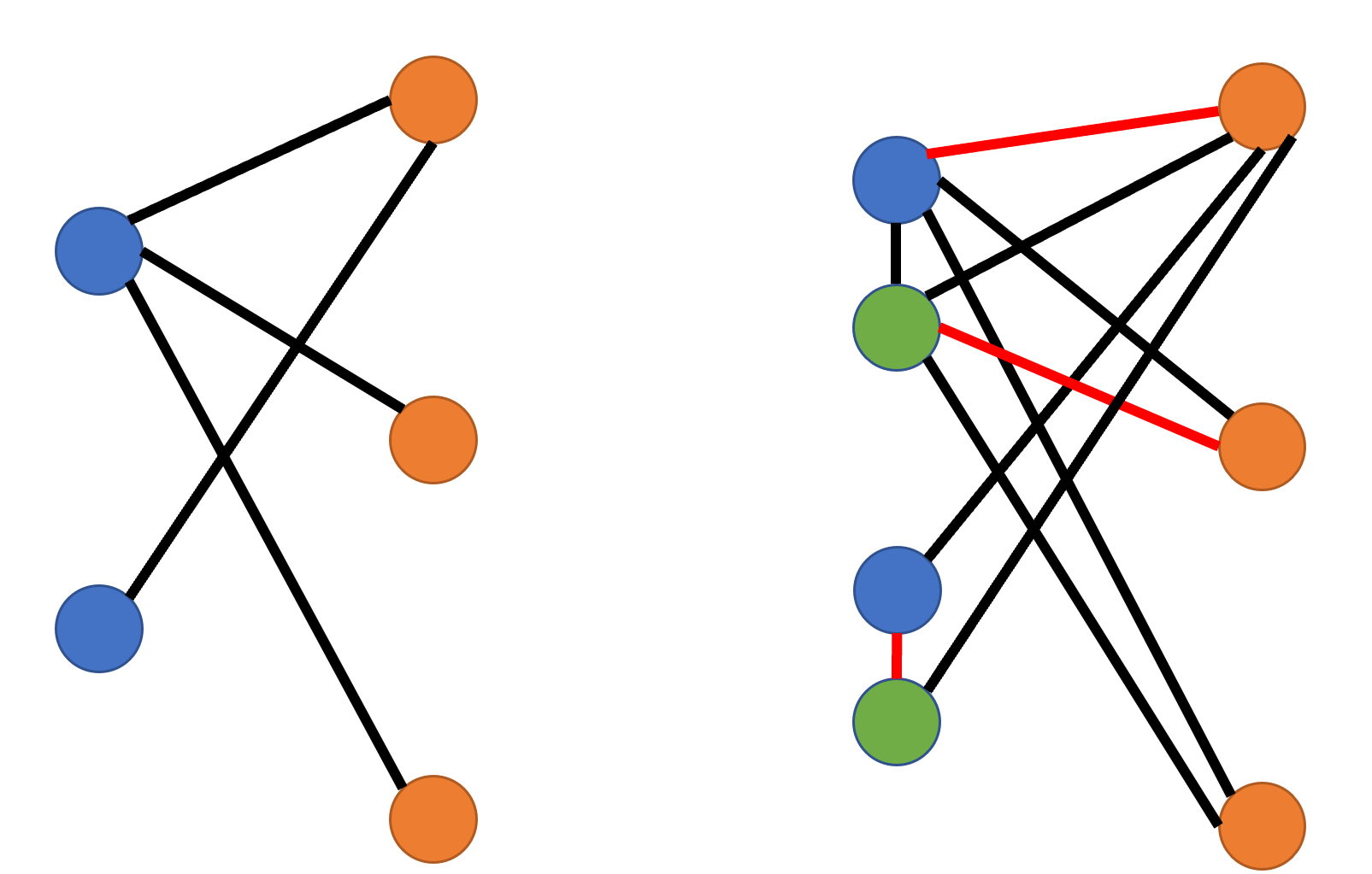
• 首先在原来二分图的基础上，将一个男生拆成两个点

• 两个点之间有一条边，这样图至少会有n个匹配

• 如果想要答案加1，只有当这两个点跟两个女生匹配的时候

• 所以最后的答案是一般图最大匹配减去n

• 一般图最大匹配用带花树

#pragma GCC optimize(3, "Ofast", "inline")

#include<bits/stdc++.h>

using namespace std;
const int maxn = 305;
const int maxm = 50050;

struct bloosom {
    struct edge {
        int to, next;
    } e[maxm];
    int tot = 0, head[maxn];

    inline void add(int u, int v) {
        ++tot;
        e[tot].to = v, e[tot].next = head[u], head[u] = tot;
        ++tot;
        e[tot].to = u, e[tot].next = head[v], head[v] = tot;
    }

    int fa[maxn], tag = 0, pre[maxn], match[maxn], q[maxn], r, fl[maxn];
    int vis[maxn], all;

    int findx(int x) {
        if (fa[x] == x)return x;
        return fa[x] = findx(fa[x]);
    }

    int lca(int u, int v) {
        ++tag;
        u = findx(u);
        v = findx(v);
        for (;; swap(u, v)) {
            if (u) {
                if (fl[u] == tag)return u;
                fl[u] = tag;
                u = findx(pre[match[u]]);
            }
        }
    }

    void blo(int u, int v, int l) {
        for (; findx(u) != l; v = match[u], u = pre[v]) {
            pre[u] = v;
            if (vis[match[u]] == 1)vis[q[++r] = match[u]] = 0;
            if (findx(u) == u) fa[u] = l;
            if (findx(match[u]) == match[u]) fa[match[u]] = l;
        }
    }

    bool aug(int s) {
        for (int j = 1; j <= all; ++j) {
            fa[j] = j;
            vis[j] = -1;
        }
        vis[q[r = 1] = s] = 0;
        int x, y;
        for (int i = 1; i <= r; ++i) {
            for (int j = head[x = q[i]]; j; j = e[j].next) {
                if (vis[y = e[j].to] == -1) {
                    pre[y] = x;
                    vis[y] = 1;
                    if (!match[y]) {
                        for (int u = x, v = y, t; u; v = t, u = pre[v]) {
                            t = match[u];
                            match[u] = v;
                            match[v] = u;
                        }
                        return 1;
                    }
                    vis[q[++r] = match[y]] = 0;
                } else if (!vis[y] && findx(x) != findx(y)) {
                    int l = lca(x, y);
                    blo(x, y, l);
                    blo(y, x, l);
                }
            }
        }
        return 0;
    }

    inline void init() {
        for (int i = 0; i <= all; ++i) {
            pre[i] = match[i] = head[i] = 0;
        }
        tot = 0;
    }

    int solve() {
        int ans = 0;
        for (int i = 1; i <= all; ++i) {
            if (!match[i]) {
                if (aug(i)) ans++;
            }
        }
        return ans;
    }
} st;

int main() {
    int _;
    scanf("%d", &_);
    while (_--) {
        int n, m, s;
        scanf("%d%d", &n, &m);
        st.all = n * 2 + m;
        st.init();

        for (int i = 1; i <= n; ++i) {
            st.add(i, i + n);
            for (int j = 1; j <= m; ++j) {
                scanf("%1d", &s);
                if (s) {
                    st.add(i, j + (n << 1));
                    st.add(i + n, j + (n << 1));
                }
            }
        }
        printf("%d\n", st.solve() - n);
    }
    return 0;
}