R语言 线性回归分析实例 《回归分析与线性统计模型》page72

y,X1,X2,X3 分别表示第 t 年各项税收收入(亿元)，某国生产总值GDP(亿元)，财政支出(亿元)和商品零售价格指数(%).

(1) 建立线性模型：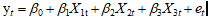

① 自己编写函数：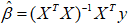

> library(openxlsx)
> data = read.xlsx("22_data.xlsx",sheet = 1)
> x = data[,-c(1,2)]
> x = cbind(rep(1,17),x)
> x_mat  = as.matrix(x)
> y =matrix(data[,2],ncol = 1)
> res = solve(t(x_mat)%*%x_mat)%*%t(x_mat)%*%y
> res
                    [,1]
rep(1, 17) 19412.8597818
X1             0.2679605
X2            -0.2874013
X3          -297.3653736

所以各参数的估计值分别为

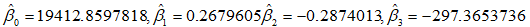
② lm函数

> lm(y~x_mat)

Call:
lm(formula = y ~ x_mat)

Coefficients:
    (Intercept)  x_matrep(1, 17)          x_matX1
19412.859781545               NA      0.267960511
        x_matX2          x_matX3
   -0.287401287   -297.365373557

于是各参数的估计值分别为

这两个方法的结果是一样的。

(2)要求实验报告中画出矩阵散点图，给出参数的点估计、区间估计、t检验值、判定系数和模型F检验的方差分析表

绘制矩阵散点图。

library(graphics)
pairs(data[,-1]pch = 21,bg = c('red','green3','blue'))
# pch参数是控制点的形状，bg是控制点的颜色

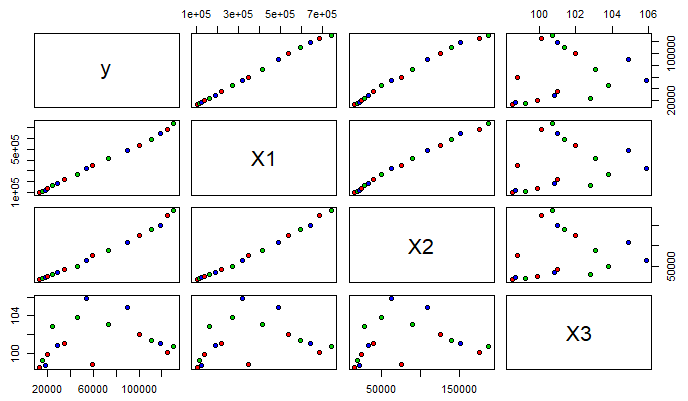
下面代码给出参数的点估计，t检验值，判定系数

> summary(lm(y~x_mat+1))

Call:
lm(formula = y ~ x_mat + 1)  #调用

Residuals:      #残差统计量，残差第一四分位数(1Q)和第三分位数(3Q)有大约相同的幅度，意味着有较对称的钟形分布
    Min      1Q  Median      3Q     Max
-4397.9 -1102.4   153.8  1184.4  2934.6 

Coefficients: (1 not defined because of singularities)
                  Estimate Std. Error t value Pr(>|t|)
(Intercept)      1.941e+04  3.524e+04   0.551    0.591
x_matrep(1, 17)         NA         NA      NA       NA
x_matX1          2.680e-01  4.466e-02   6.000 4.45e-05 ***
x_matX2         -2.874e-01  1.668e-01  -1.723    0.109
x_matX3         -2.974e+02  3.688e+02  -0.806    0.435
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#标记为Estimate的列包含由最小二乘法计算出来的估计回归系数。
#标记为Std.Error的列是估计的回归系数的标准误差。
#从理论上说，如果一个变量的系数是0，那么该变量将毫无贡献。然而，这里显示的系数只是估计，它们不会正好为0.
#因此，我们不禁会问：从统计的角度而言，真正的系数为0的可能性有多大？这是t统计量和P值的目的，在汇总中被标记为t value和Pr(>|t|)
#P值估计系数不显著的可能性，有较大P值的变量是可以从模型中移除的候选变量

Residual standard error: 2013 on 13 degrees of freedom
Multiple R-squared:  0.9982,	Adjusted R-squared:  0.9977
F-statistic:  2348 on 3 and 13 DF,  p-value: < 2.2e-16

#Residual standard error 表示残差的标准差，F-statistic 表示F的统计量

　　区间估计？方差分析表？

#参数的区间估计
fm = lm(y~x_mat)
confint(fm,level = 0.95)
anova(fm) #方差分析

(3)保留模型中线性关系显著的预测变量确定最后的模型，并利用R软件中的"predict"语句预测2017年的税收收入

根据回归分析结果，只有变量X1具有显著性。所以模型中仅保留变量X1。

构造模型：

x_mat = cbind(rep(1,17),data[,3])
y = data[,2]
res = lm(y~x_mat)
res
> res

Call:
lm(formula = y ~ x_mat)

Coefficients:
(Intercept)       x_mat1       x_mat2
 -6213.0189           NA       0.1915

该模型为：Y = -6213.0189 + 0.1915 X1

接下来预测2017年的税收收入，先根据数据data对 t 和 y 之间的关系进行回归分析

t = data[,1]
y = data[,2]
res = lm(y~t)
res

> res

Call:
lm(formula = y ~ t)

Coefficients:
(Intercept)            t
  -16428607         8213  

所以 t 与 y 的关系为：y  = -16428607 + 8213 t

预测 2017 年的税收收入：

> newdata = data.frame(t = 2017)
> pre = predict(res,newdata,interval = "prediction",level = 0.95)
> pre
       fit      lwr      upr
1 136337.8 116018.1 156657.4

　　

（4）方差齐性检验，正态性检验，误差相关性的DW检验

rm(list = ls())
library(openxlsx)
data = read.xlsx("22_data.xlsx",sheet = 3)
data
attach(data) #执行此命令之后，直接用列名引用数据
fm = lm(y~X1+X2+X3)
summary(fm)

　　

#残差图：方差齐性检验
ei = resid(fm) #残差
X = cbind(1,as.matrix(data[,3:5])) #创建设计阵，注意as.matrix的对象
t = ti(ei,X) #外部学生化残差
r = ri(ei,X) #学生化残差
plot(fitted(fm),t,xlab = "y估计值",ylab = "学生化残差",ylim = c(-4,4))
abline(h = 0)

　　

1)上图表示，围绕x轴上下波动，不是均匀分布，方差不齐，但是这个残差图代表什么呢？
2)第17个点是异常点

#正态概率图：正态性检验
plot_ZP(t)

　　

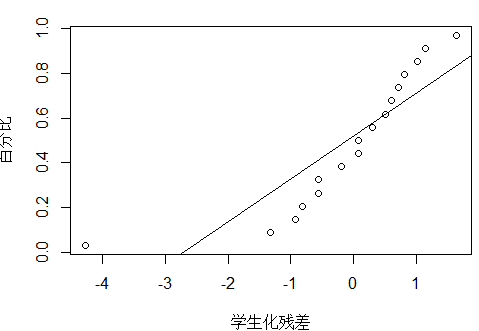
除了17号点，其他的点基本在一条直线。

plot_ZP(t[1:16])

　　

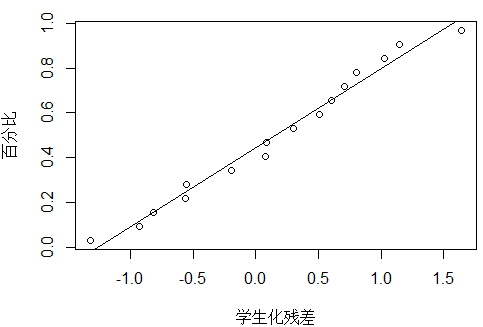
#误差相关性的DW检验
library(lmtest)
dw = dwtest(fm) #DW检验函数

> dw

Durbin-Watson test

data: fm
DW = 0.90086, p-value = 0.0006763
alternative hypothesis: true autocorrelation is greater than 0

p值远小于0.05，拒绝原假设ρ=0，所以误差是自相关的

plot(ei) #绘制时间序列中的残差图
abline(h = 0)

　　

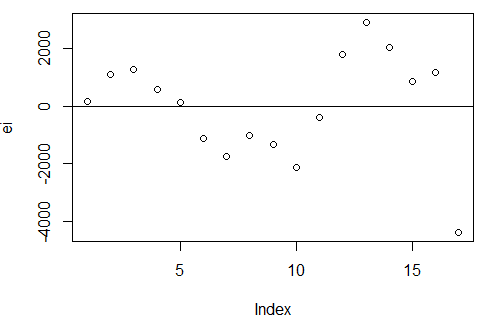
图像表明：误差是正自相关的。
正自相关：如果前一个残差大于0，那么后一个残差大于0的概率较大
负自相关：富国前一个残差大于0，那么后一个残差小于0的概率较大

（4）强影响点分析，异常点分析

#强影响点分析
#方法：手指律、刀切法、cook距离、deffits
#influence.measures(fm)
influence.measures(fm)
# 函数得到的回归诊断共有9列，
# 其中1,2,3,4列是dfbetas值（对应常数与变量x），
# 第5列是dffits的准则值，
# 第6列是covratio的准则值,
# 第7列是cook值,第8列是帽子值（高杠杆值），
# 第9列是影响点的标记，
# inf表明16，17号是强影响点。

　　

#cook距离判断强影响点
res = cooks.distance(fm)
> res[res>4/(17-3-1)]
      17
1.266196
> #17号是强影响点

　　

#异常点
#方法：dfbetas、F统计量、outlierTest()
library(car)
outlierTest(fm)

    rstudent unadjusted p-value Bonferroni p
17 -4.277398          0.0010739     0.018257

Bonferroni p < 0.05 , 结果显示17号点是异常点

　　

#使用influencePlot()将异常点绘入图中
influencePlot(fm)

　　

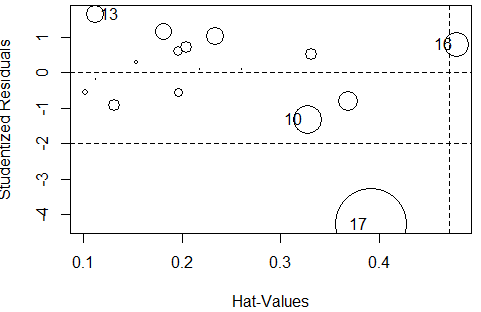
#F统计量page88
calcu_F = function(p,r) #p回归参数个数，r学生化残差
{
  n = length(r)
  ans = (n-p-2)*(r**2)/(n-p-1-r**2)
  return(ans)
}
ff = calcu_F(3,r)
#与自由度为1,n-p-2,显著性水平为α的F值比较
df_val = qf(1-0.05,1,12)

ff[ff>df_val] #检验显著性
      17
18.29613

　　

（6）模型失拟检测

模型失拟检测
1.有重复值用失拟检测的正规检验《线性回归导论》
2.无重复值
1）当模型的预测变量个数多余1时，考虑偏残差法
2）无论预测变量个数，近邻点估计纯误差方法都可以

# 偏残差：
data
beta = coef(fm)
beta1 = beta[2]
beta2 = beta[3]
beta3 = beta[4]
#第一个预测变量：
par(mfrow = c(2,2))
cancha1 = ei + beta1*(data$X1)
plot(data$X1,cancha1)
#第二个预测变量：
cancha2 = ei + beta2*(data$X2)
plot(data$X2,cancha2)
#第三个预测变量：
cancha3 = ei + beta3*(data$X3)
plot(data$X3,cancha3)
#通过图像，第三个预测变量不