SVM家族（一）

SVM家族简史

故事要从20世纪50年代说起，1957年，一个叫做感知器的模型被提出，

1963年， Vapnikand Chervonenkis, 提出了最大间隔分类器，SVM诞生了。

1992年，Vapnik 将核方法用于SVM，使SVM可以处理线性不可分数据

1995年，Corts和Vapnik引入了软间隔，允许SVM犯一些错

最强版SVM出现了，它将各式武学集于一身，软间隔、核方法、……，

1996年，SVR（support vector regression）诞生，svm家族又添一员，回归任务也不在话下。至此，SVM家族成为机器学习界顶级家族之一。关于SVM家族其他成员，可以参阅这里。

SVM是什么？

• 是一种监督学习分类算法，可以用于分类/回归任务
• SVM目标：寻找最优分割超平面以最大化训练数据的间隔

什么是超平面？

• 在一维空间，超平面是一个点
• 二维空间，超平面是一条线
• 三维空间，超平面是一个平面
• 更多维空间，称为超平面

什么是最优分割超平面？

• 尽可能远离每一个类别的样本点的超平面
  • 首先，可以正确的将训练数据分类
  • 其次，拥有更好的泛化能力

那么如何找到这个最优超平面呢？根据间隔

什么是间隔？

给定一个超平面，超平面到最近的样本点之间的距离的2倍称为间隔。

在最初的SVM中，间隔是一个强定义，即硬间隔，间隔之间不允许存在任何样本。（当数据中存在噪音时，会产生一些问题，所以后来软间隔被引入）

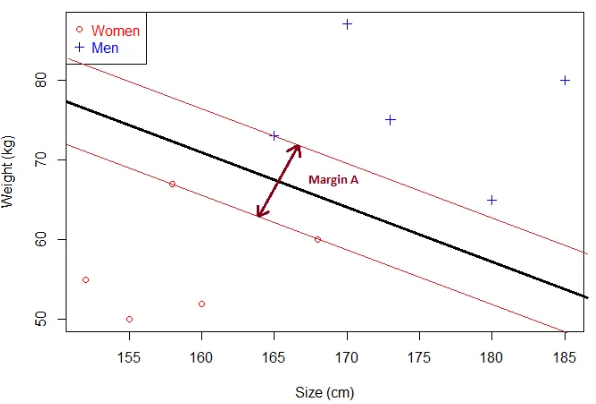
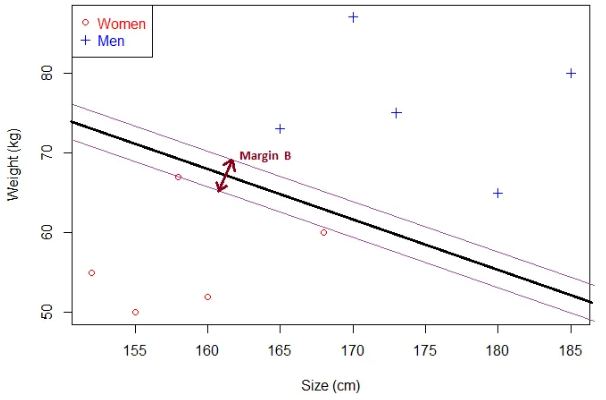
显然，间隔B小于间隔A。可知：

• 如果超平面越接近样本点，对应的间隔越小
• 超平面离样本点越远，间隔越大

所以最优超平面对应最大间隔，SVM就是围绕着这个间隔展开，如何计算这个间隔？