简述N种排序算法

排序算法概述

　　排序算法是程序员日常很常见的算法，基本上每天都会使用排序，在这里将进行一下总结。

　　排序算法大致可分为比较类排序和非比较类排序二种，其核心区别可以简单的理解为非比较类排序是对比较类排序之前进行了一层包装，也就是说排序的核心操作依然还是比较。

　　目前主流的排序算法根据分类可以分成下图所示：

　　

　　

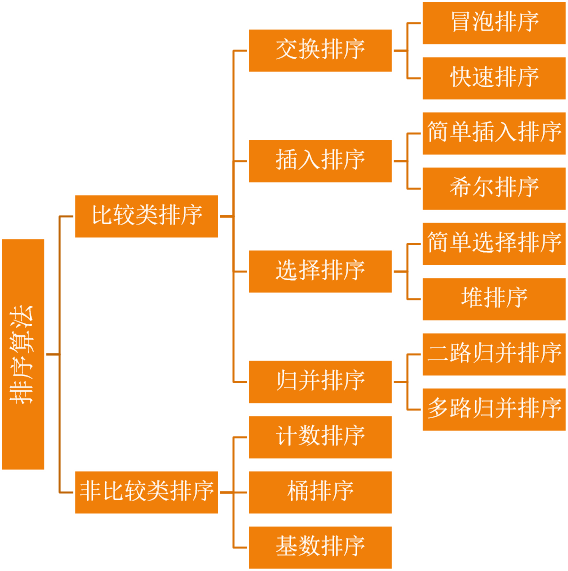
简述比较类排序

　　冒泡排序

　　冒泡排序是一种老生常谈也是作为一种入门级的排序算法，其逻辑较为简单粗暴，即每次比较相邻的两个元素，如果顺序不符合就交换位置，一直不断的重复直到全部满足则停止。

　　算法步骤如图所示：

　　

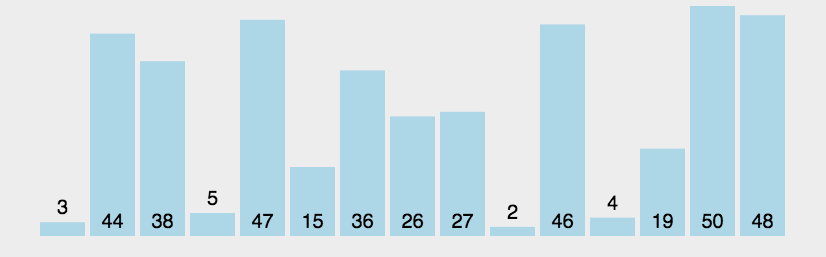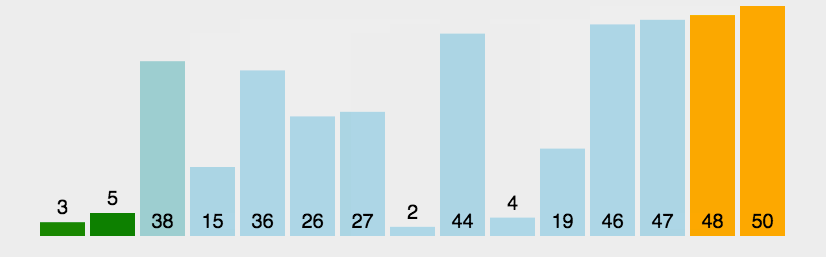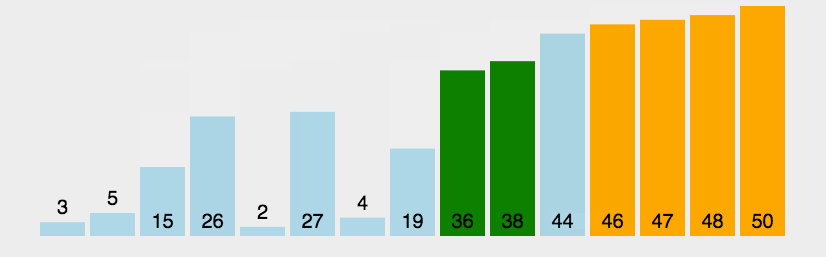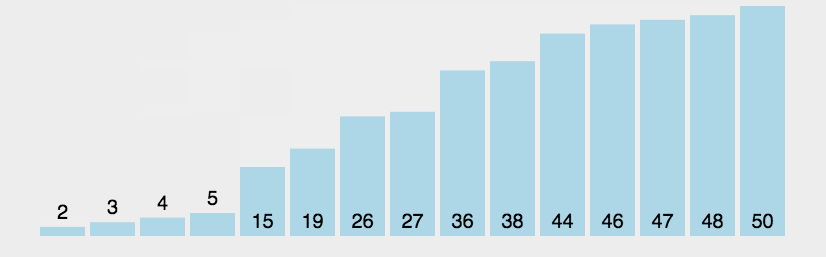
　　性能：

　　

　　代码实现：

　　

  public class BubbleSort
     {
         public static List<int> Demo(List<int> data)
         {
             ///你要想看一个人的排序算法什么的写的好不好,主要看他的OP个数
             ///
             //4+4+4+4+4=>20字节
             for (var i = ; i < data.Count; i++)//i
             {
                 for (var j = ; j < data.Count -  - i; j++)//j
                 {
                     if (data[j] > data[j + ])
                     {
                         var temp = data[j + ];///空间复杂度
                         //J+1-->多了一个
                         data[j + ] = data[j];//->j+1-->
                         data[j] = temp;
                     }
                 }
             }
             return data;
         }
     }

BubbleSort

　　

　　快速排序

　　由刚刚的冒泡排序可以知道冒泡排序进行了太多次的重复步骤，快排就对这个事情进行了一定的改进。

　　快排的实现原理也十分简单，首先挑选一个基准数字，然后把比基准数字大的数字都放到一边，然后在这个分区退出后,该基准就应该在数列中间的位置,把这个操作,成为”分区”.

　　完事以后,再基于基准值元素进行子数列排序就好了.

　　算法步骤如图所示：

　　

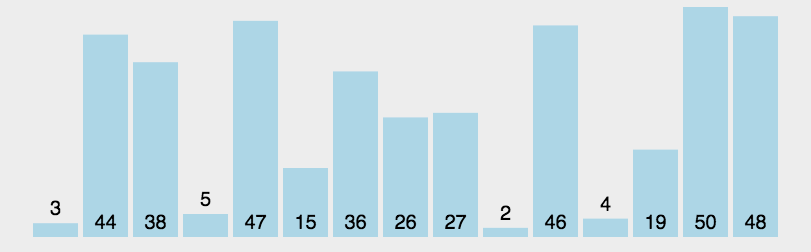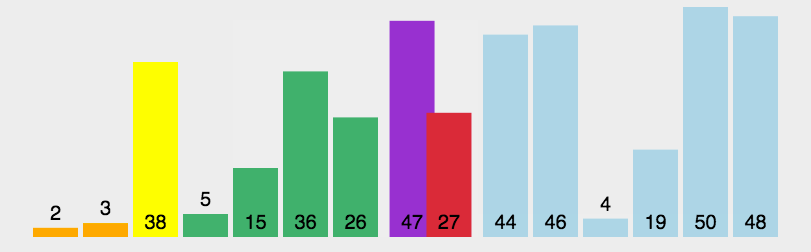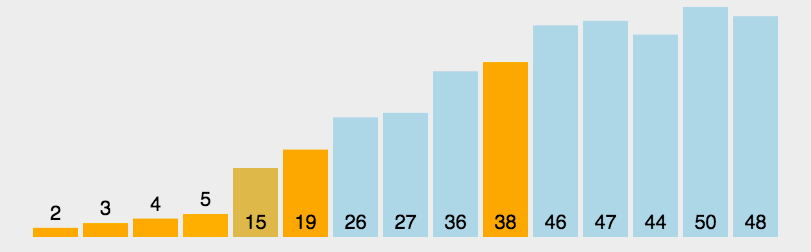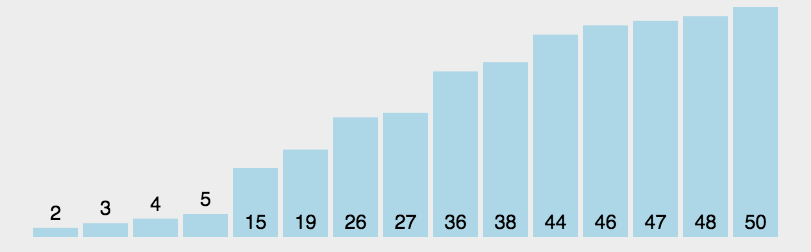
　　性能：

　　

　　代码：

　　

   public class QuickSort
     {
         //排序算法--->  遍历-->判断                    --->交换<-------降低
         public static List<int> Demo(List<int> data, int left = , int? right = null)
         {
             int len = data.Count, partitionIndex;
             right = right ?? data.Count - ;
             if (left < right)
             {
                 partitionIndex = partition(data, left, right.Value);
                 Demo(data, left, partitionIndex - );
                 Demo(data, partitionIndex + , right);
             }
             return data;
         }
         //分块的  左边是啥??? 右边是啥??
         static int partition(List<int> data, int left, int right)
         {
             int pivot = left, index = pivot + ;
             for (var i = index; i <= right; i++)
             {
                 if (data[i] < data[pivot])
                 {
                     Swap(data, i, index);///交换i跟index
                     index++;
                 }
             }
             Swap(data, pivot, index - );///交换pivot与index-1
             return index - ;
         }

         static void Swap(List<int> data, int i, int j)
         {
             var temp = data[i];
             data[i] = data[j];
             data[j] = temp;
         }
     }

QuickSort

简单插入排序

　　简单插入排序也是一个十分简单的排序，比较容易相像，即拿一个元素出来，看看应该丢哪，然后丢过去即可

　　原理如图：

　　

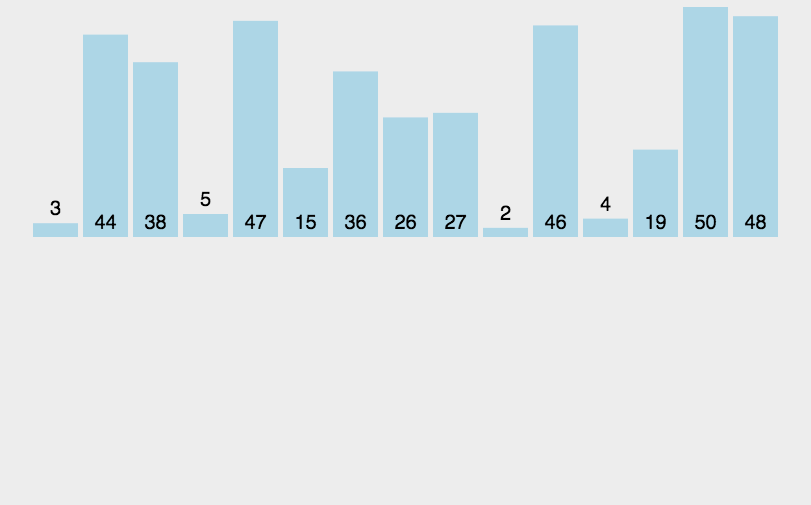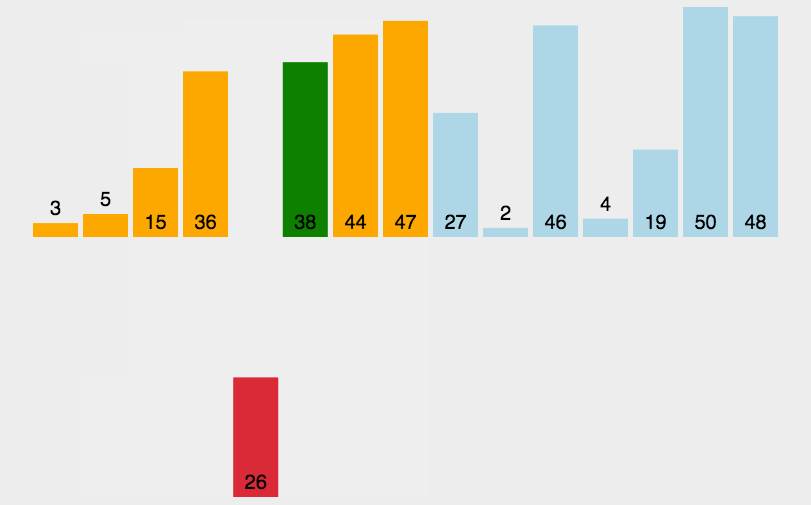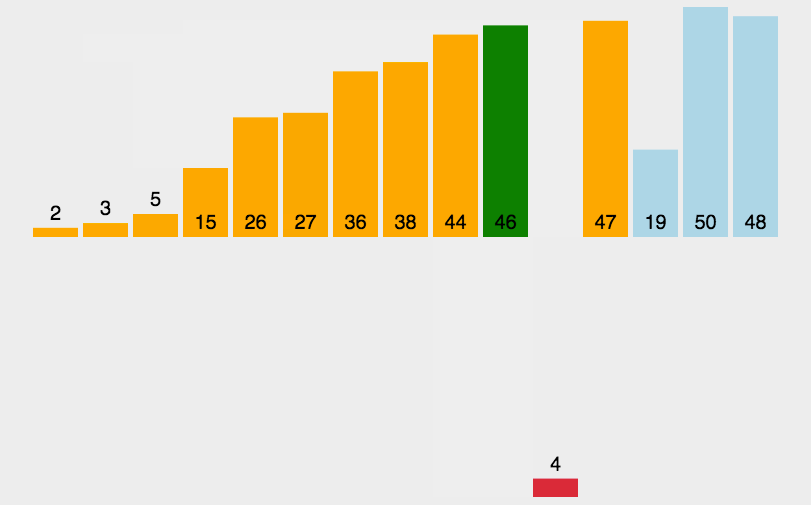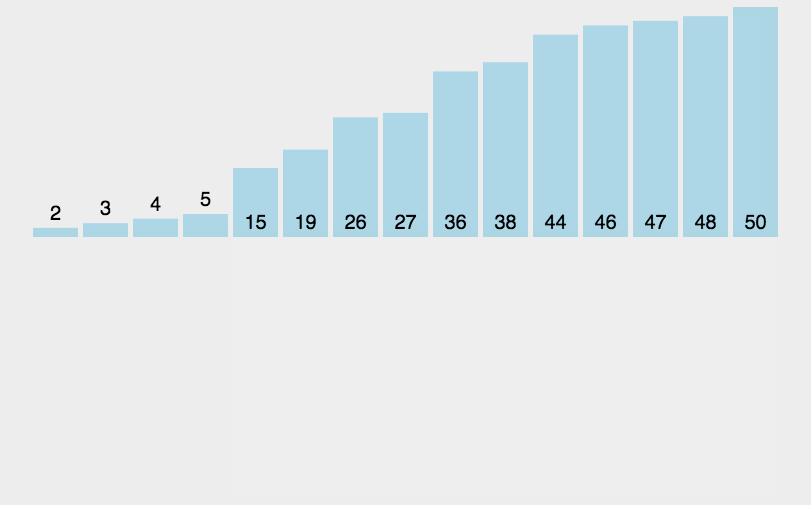
　　性能：

　　

　　代码：

　　

   public class InsertSort
     {
         public static List<int> Demo(List<int> data)
         {
             int preIndex, currentIndex;
             for (var i = ; i < data.Count; i++)
             {
                 preIndex = i - ;
                 currentIndex = data[i];
                 while (preIndex >=  && data[preIndex] > currentIndex)
                 {
                     data[preIndex + ] = data[preIndex];
                     preIndex--;
                 }
                 data[preIndex + ] = currentIndex;
             }
             return data;
         }
     }

InsertSort

希尔排序

　　这个相对于之前的排序会稍微复杂一点，步骤如下：

　　　　1.先把整个序列分成N个子序列.随便选一个序列xyz...增量的哦最好.

　　　　2.刚才那个序列增量序列排序一下,直接插入排序

　　　　3.循环刚才的事情.然后往前移动.一边移动一边输出.

　　按图来说就是第一遍循环的时候中间间隔4个，第二遍的时候间隔1个，第三遍的时候紧挨着然后将数移动到合适的位置

　　如图所示：

　　

　　性能：

　　

　　代码：

　　

  public class ShellSort
     {
         public static List<int> Demo(List<int> data)
         {
             for (int gap =(int) Math.Floor(((decimal)(data.Count / ))); gap > ; gap = (int)Math.Floor(((decimal)(gap / ))))
             {
                 for (var i = gap; i < data.Count; i++)
                 {
                     var j = i;
                     var current = data[i];
                     while (j - gap >=  && current < data[j - gap])
                     {
                         data[j] = data[j - gap];
                         j = j - gap;
                     }
                     data[j] = current;
                 }
             }
             return data;
         }
     }

ShellSort

　　

简单选择排序

　　这个和简单插入有点像但是略有不同。

　　简单选择排序过程为：

　　　　1.找一个最大/小的.

　　　　2.放到最后/前.

　　　　3.重复并慢慢缩小范围

　　和简单插入不同在于简单选择先找了最大最小值而简单插入为按顺序一个一个取值。

　　如图：

　　

　　性能：

　　

　　代码：

　　

   public class SelectSort
     {
         public static List<int> Demo(List<int> data)
         {
             int minIndex, temp;
             for (var i = ; i < data.Count - ; i++)
             {
                 minIndex = i;
                 for (var j = i + ; j < data.Count; j++)
                 {
                     if (data[j] < data[minIndex])
                     {
                         minIndex = j;
                     }
                 }
                 temp = data[i];
                 data[i] = data[minIndex];
                 data[minIndex] = temp;
             }
             return data;
         }
     }

SelectSort

　

堆排序

　　这个相对而言比较复杂，实现步骤如下：

　　1.先随便组合成一个二叉树.

　　 2.比较相邻二个数大小来交换相邻的二个节点的顺序，将最大的值向上推，

　　也就是说父节点大于下面2个各自的子节点而子节点哪个大暂时不关心。

　　3.将最大的根节点挪移到右下角节点并断开该节点与未排序树的连接

　　4.重复操作到所有节点均断开连接即排序完成。

　　如图所示：

　　

　　性能：

　　

　　代码：

　　

   public class HeapSort
     {
         static int _count;    

         public static List<int> Demo(List<int> data)
         {
             Build(data);

             for (var i = data.Count - ; i > ; i--)
             {
                 Swap(data, , i);
                 _count--;
                 Heapify(data, );
             }
             return data;
         }
         static void Build(List<int> data)
         {   // 建立大顶堆
             _count = data.Count;
             for (var i = (int)Math.Floor(((decimal)(_count / ))); i >= ; i--)
             {
                 Heapify(data, i);
             }
         }

         static void Heapify(List<int> data, int i)
         {
             int left =  * i + ,
             right =  * i + ,
             largest = i;

             if (left < _count && data[left] > data[largest])
             {
                 largest = left;
             }

             if (right < _count && data[right] > data[largest])
             {
                 largest = right;
             }

             if (largest != i)
             {
                 Swap(data, i, largest);
                 Heapify(data, largest);
             }
         }

         static void Swap(List<int> data, int i, int j)
         {
             var temp = data[i];
             data[i] = data[j];
             data[j] = temp;
         }

     }

HeapSort

归并排序

　　归并排序分为二路归并和多路归并，其实本质思路是一个思路，区别只在于同时有几个并行归并操作而已。

　　步骤如下：

　　1.根据你的要求分成你喜欢的数量，形成一个个分区

　　2.然后每个分区各自排序

　　3.完事之后合并排序结果，这个步骤类似于合并二个集合，有种学校里学的集合之间合并的感觉。

　　如图所示：

　　

　　性能：

　　

　　代码：

　　

   public class MergeSort
     {
         //P=NP:
         public static List<int> Demo(List<int> data)
         {
             var arr = data.ToArray();
             if (data.Count < )
             {
                 return data;
             }
             int middle = (int)Math.Floor(((decimal)(data.Count / )));
             var left = arr.AsSpan().Slice(, middle).ToArray();
             var right = arr.AsSpan().Slice(middle).ToArray();
             return Merge(Demo(left.ToList()), Demo(right.ToList()));
         }

         static List<int> Merge(List<int> left, List<int> right)
         {
             var result = new List<int>();

             while (left.Count >  && right.Count > )
             {
                 if (left[] <= right[])
                 {
                     result.Add(left[]);
                     left.RemoveAt();
                 }
                 else
                 {
                     result.Add(right[]);
                     right.RemoveAt();
                 }
             }

             while (left.Count != )
             {
                 result.Add(left[]);
                 left.RemoveAt();
             }

             while (right.Count != )
             {

                 result.Add(right[]);
                 right.RemoveAt();
             }

             return result;
         }
     }

MergeSort

非比较类排序

计数排序

　　这个方案也较为简单粗暴，步骤如下：

　　1.选取最大最小的极值

　　2.遍历一遍数组，将各个数字出现的次数记录下来

　　3.根据大小和次数直接生成排序后集合。

如图所示：

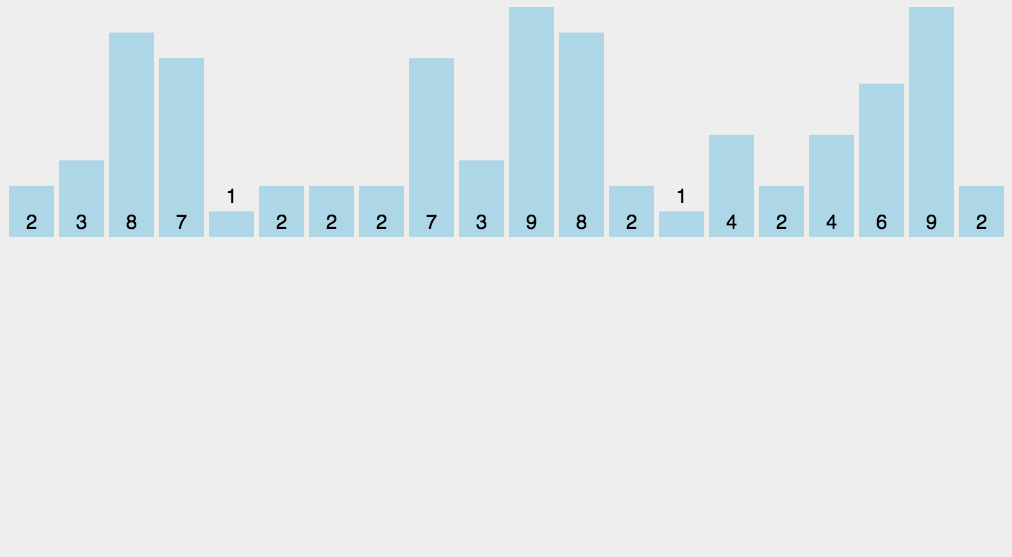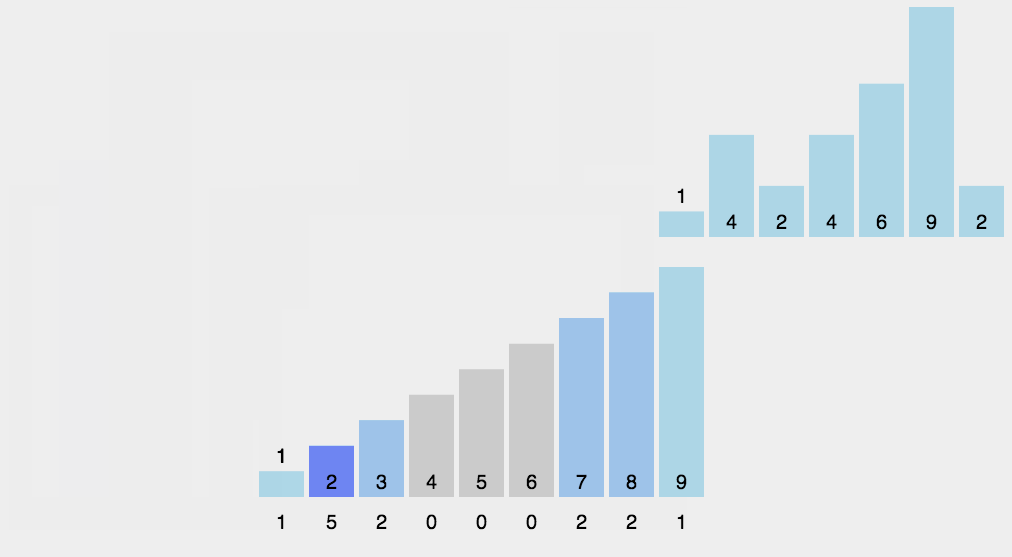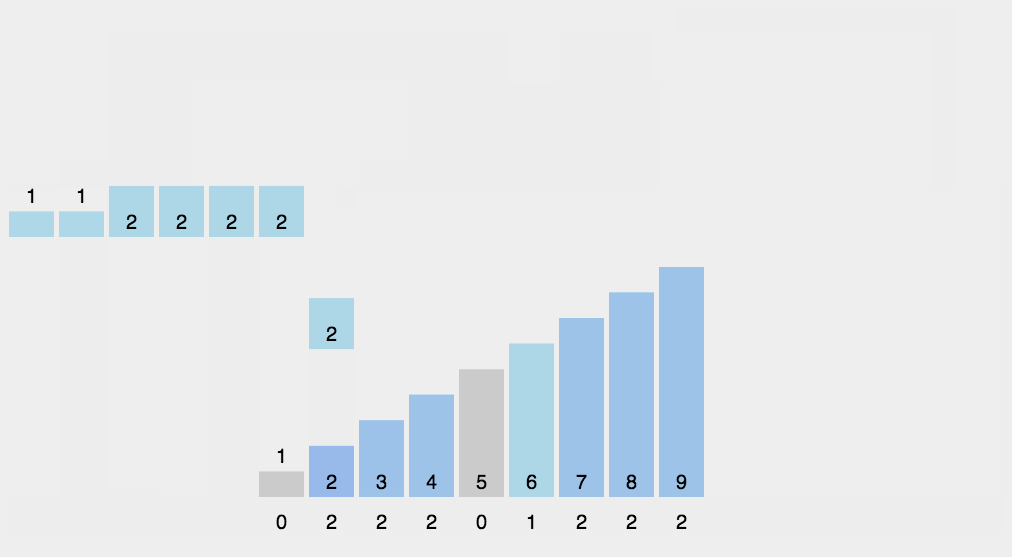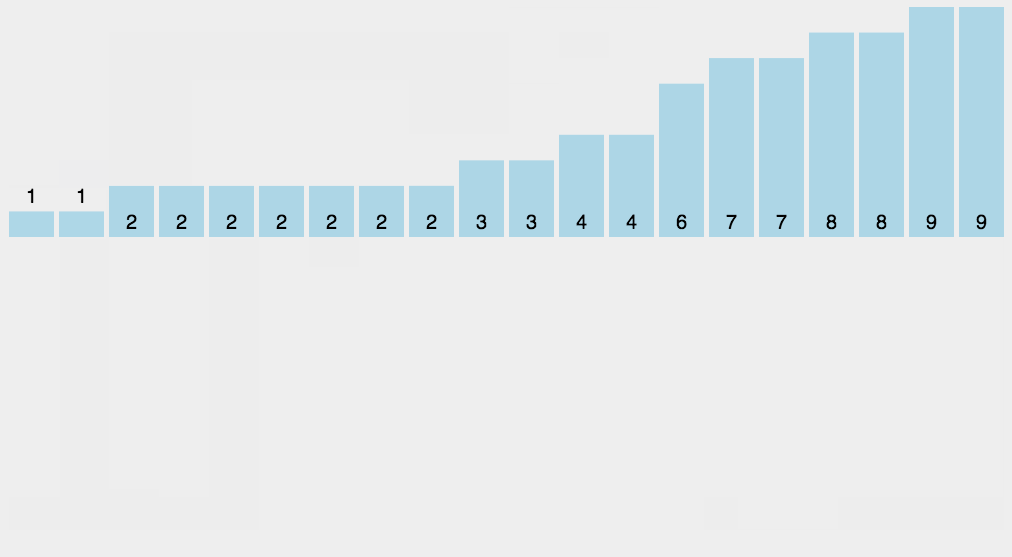
　　性能：

　　

　　代码：

　　

   public class CountingSort
     {
         public static List<int> Demo(List<int> data)
         {
             var maxValue = data.Max();
             var bucket = new int[maxValue + ];
             int sortedIndex = ;
             int bucketLen = maxValue + ;
             for (var i = ; i < data.Count; i++)
             {
                 if (bucket[data[i]] != )
                 {
                     bucket[data[i]] = ;
                 }
                 bucket[data[i]]++;
             }

             for (var j = ; j < bucketLen; j++)
             {
                 while (bucket[j] > )
                 {
                     data[sortedIndex++] = j;
                     bucket[j]--;
                 }
             }

             return data;
         }
     }

CountingSort

桶排序

　　针对计数排序进行了改造，步骤如下：

　　1.预估数据平均大概需要多少个范围容器以及每个容器大概会有多少数据

　　2.遍历数据，根据数据所在的区间范围丢到对应的桶里

　　3.排序桶

　　4.合并数据

　　如图：

　　

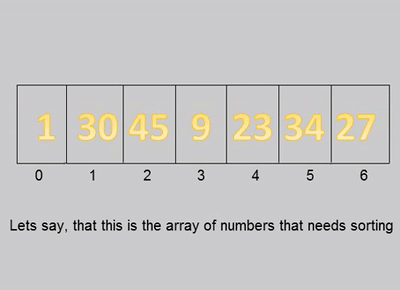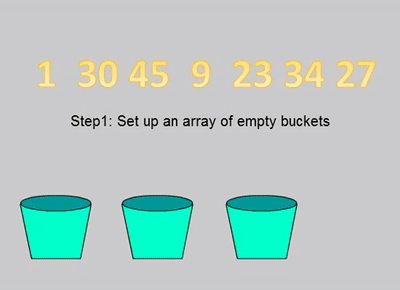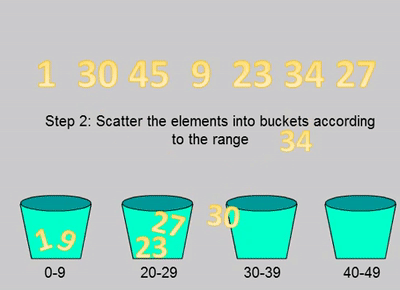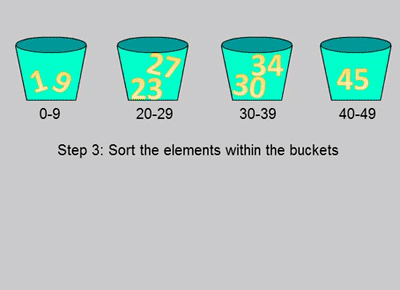
　　性能：

　　

　　代码：

　　

   public class BucketSort
     {
         public static List<int> Demo(List<int> data)
         {
             if (data.Count == )
             {
                 return data;
             }

             var minValue = data[];
             var maxValue = data[];
             for (var i = ; i < data.Count; i++)
             {
                 if (data[i] < minValue)
                 {
                     minValue = data[i];
                 }
                 else if (data[i] > maxValue)
                 {
                     maxValue = data[i];
                 }
             }

             var bucketSize = ;
             int bucketCount = (int)Math.Floor(((decimal)((maxValue - minValue) / bucketSize))) + ;
             var buckets = new List<int>[bucketCount];
             for (var i = ; i < buckets.Length; i++)
             {
                 buckets[i] = new List<int>();
             }

             for (var i = ; i < data.Count; i++)
             {
                 buckets[(int)Math.Floor(((decimal)((data[i] - minValue) / bucketSize)))].Add(data[i]);
             }

             var res = new List<int>();
             for (var i = ; i < buckets.Length; i++)
             {
                 BubbleSort.Demo(buckets[i]);
                 for (var j = ; j < buckets[i].Count; j++)
                 {
                     res.Add(buckets[i][j]);
                 }
             }

             return res;
         }
     }

BucketSort

基数排序

　　这个排序比较骚的地方就在于运用了数理知识，实现逻辑如下：

　　1.根据每个数的个位进行排序

　　2.然后根据十位数进行排序

　　用桶的思维去看就是总共一定会有10个桶，每次根据不同的规则丢到不同的桶

　　以2位数为例，由于第一遍的时候所有个位数的数据均排好了顺序，当排好十位数的时候，所有数字顺序就全对上了。

　　如图：

　　

　　性能：

　　

　　代码：

　　

   public class RadixSort
     { 

         public static List<int> Demo(List<int> data)
         {
             var maxDigit = data.Count;
             var mod = ;
             var dev = ;
             for (var i = ; i < maxDigit; i++, dev *= , mod *= )
             {
                 Dictionary<int, List<int>> _counter = new Dictionary<int, List<int>>();
                 for (var j = ; j < data.Count; j++)
                 {
                     var bucket = ((data[j] % mod) / dev);
                     if (!_counter.ContainsKey(bucket))
                     {
                         _counter[bucket] = new List<int>();
                     }
                     _counter[bucket].Add(data[j]);
                 }
                 var pos = ;
                 for (var j = ; j <= _counter.Count; j++)
                 {
                     if (_counter.ContainsKey(j))
                     {
                         while (_counter[j].Count != )
                         {
                             data[pos++] = _counter[j][];
                             _counter[j].RemoveAt();
                         }
                     }
                 }
             }
             return data;
         }

     }

RadixSort

算法比较

　　

　　

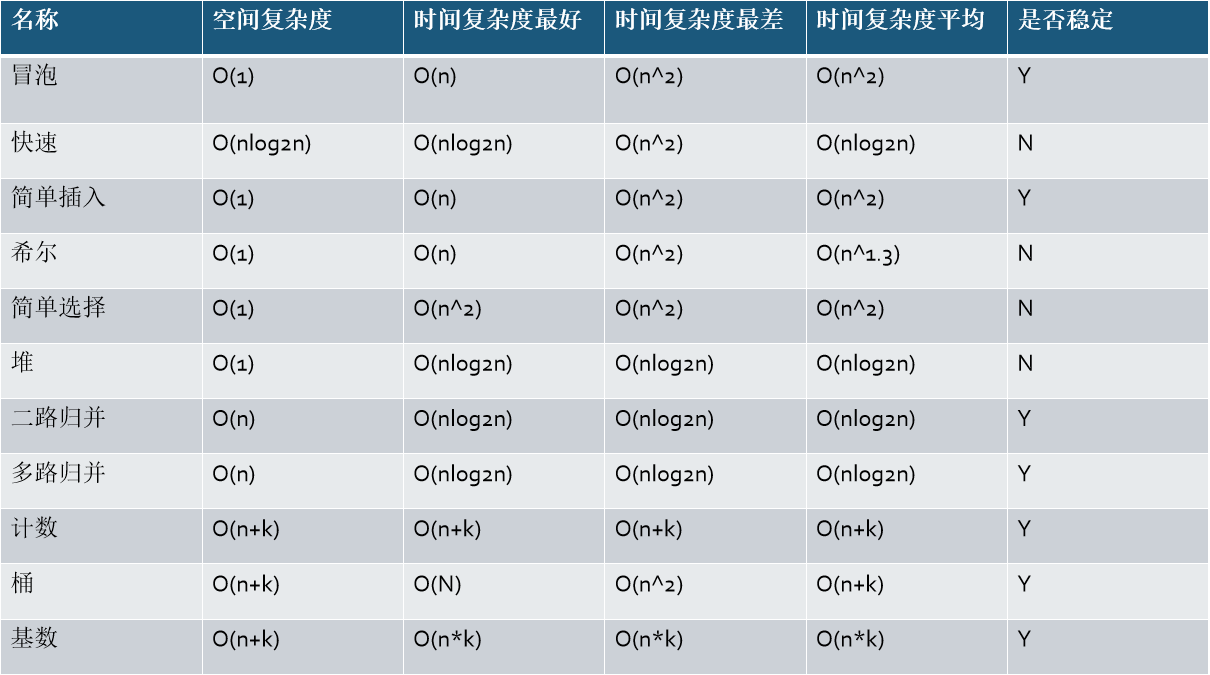
　　算法的稳定性是什么?

　　简单而言：如果两个元素值一样,分别用A,B来称呼，排序后这二个元素顺序还是AB而不是BA那就是稳定的。

　　时间复杂度是什么?

　　以白话而言:排序的操作总次数,当数据的个数N变化是,操作次数是啥样子的.

　　空间复杂度是什么?

　　拿人话说:这算法在算的时候,要申请的内存大小.也就是相对于N的话的多少.所以最少也是O(1)

　　ps:学习参考源自ben，如有错误，轻拍。