聚类算法在 D2C 布局中的应用

1.摘要

聚类是统计数据分析的一门技术，在许多领域受到广泛的应用，包括机器学习、数据挖掘、图像分析等等。聚类就是把相似的对象分成不同的组别或者更多的子集，从而让每个子集的成员对象都有相似的一些属性。

所谓聚类算法，其实就是将一对没有标签的数据自动划分成几类的方法。在应用场景上，聚类能帮助我们解决很多计算机中的分类问题，常见的如：颜色类别分类、空间坐标中的密度分类、电商中的人群特征分类。除了分类问题外，它也能帮助我们实现“异常检查”，什么是异常检查？我们可以理解为找噪点，通俗来说就是在一锅粥里面找出那些老鼠屎。

本篇文章主要是给大家介绍聚类算法的实现原理以及聚类算法是如何应用在 D2C 设计稿生成代码中。

2 DBSCAN 聚类算法

DBSCAN - 具有噪声的基于密度的聚类算法。和 K-Means 这种只适合凸样本集的聚类相比，DBSCAN 既可以凸样本集，也适用于非凸样本集。它可以对散乱的样本基于一定的相似性进行分类，即在不确定蔟数目的情况下，根据样本的紧密程度进行蔟的划分。举个例子：

我们需要把“100、101、123、98、200、203、220”这堆数据进行聚类。成蔟最小值为 2的话，

此时如果我们设置的聚类密度阈值为 30。那么“100、101、123、98” 和 “200、203、220”将会分成 2 蔟。

当聚类密度阈值为 10。那么“100、101、98”、“200、203”、分成 2 个蔟，“123”、“220”则属于噪声点（异常数据）

2.1 核心思想

DBSCAN 算法主要是找出样本点中所有的密集区域，我们称这些密集区域为聚类蔟。那么不在密集区域内的样本点，我们称为噪声点。所以 DBSCAN 除了能帮你做分类外，也能找出“一锅粥里面的老鼠屎”。

2.2 算法参数

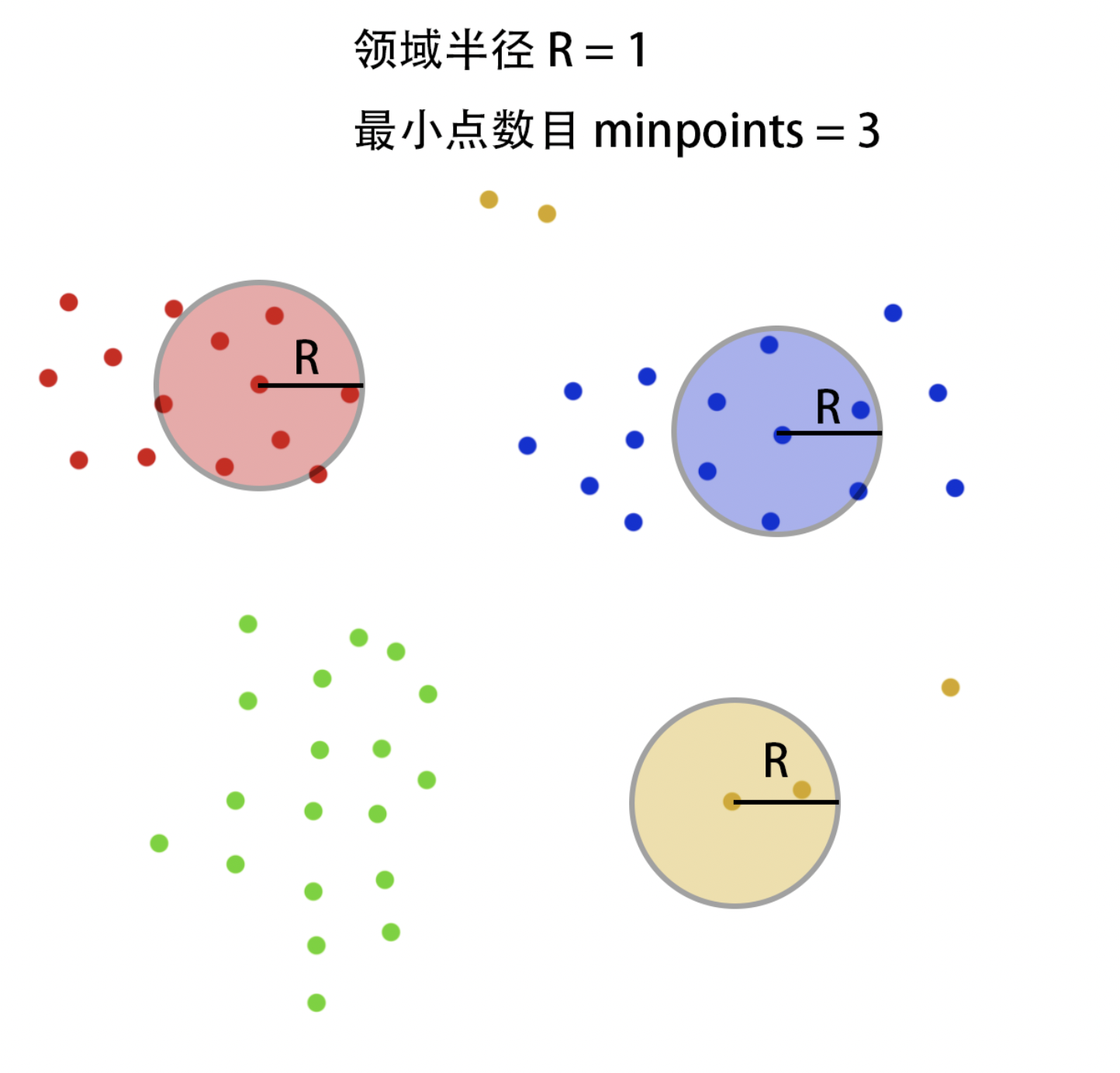
参数	说明
邻域半径 Eps：	指的是每个样本点的搜索半径，在搜索半径内扫描到的其他样本点，我们可以理解为被扫描到的样本点与中心点是相近的。
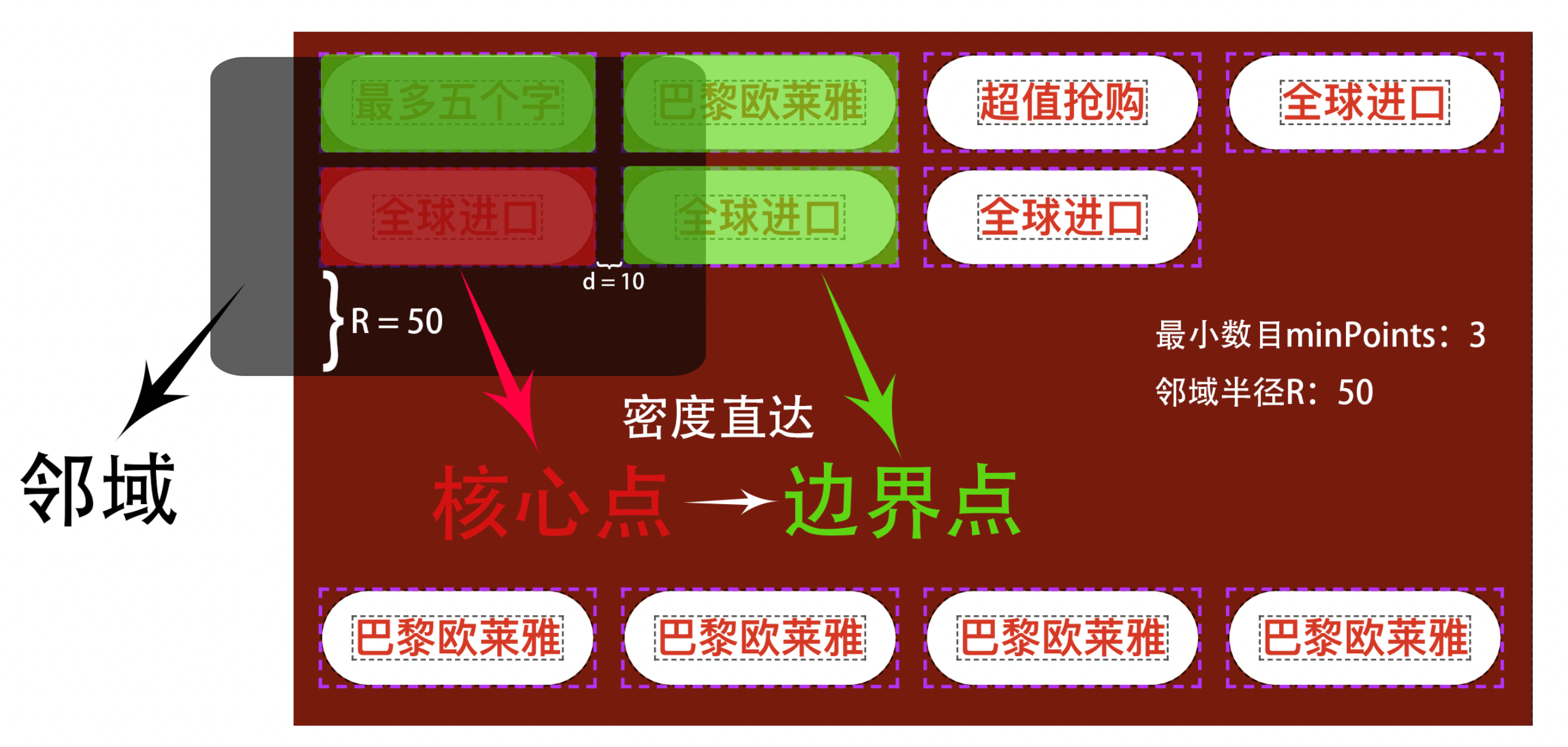
最小点数目 minpoints：	能聚合成簇的最小样本数目，可以理解为每个蔟需要的最少样本数。在上图上，我们可以看到红色、蓝色在半径 R 内均扫描到的样本点>最小点数目 minpoints，而黄色仅扫描的数量比 minpoints 要少。

2.3 点的类别

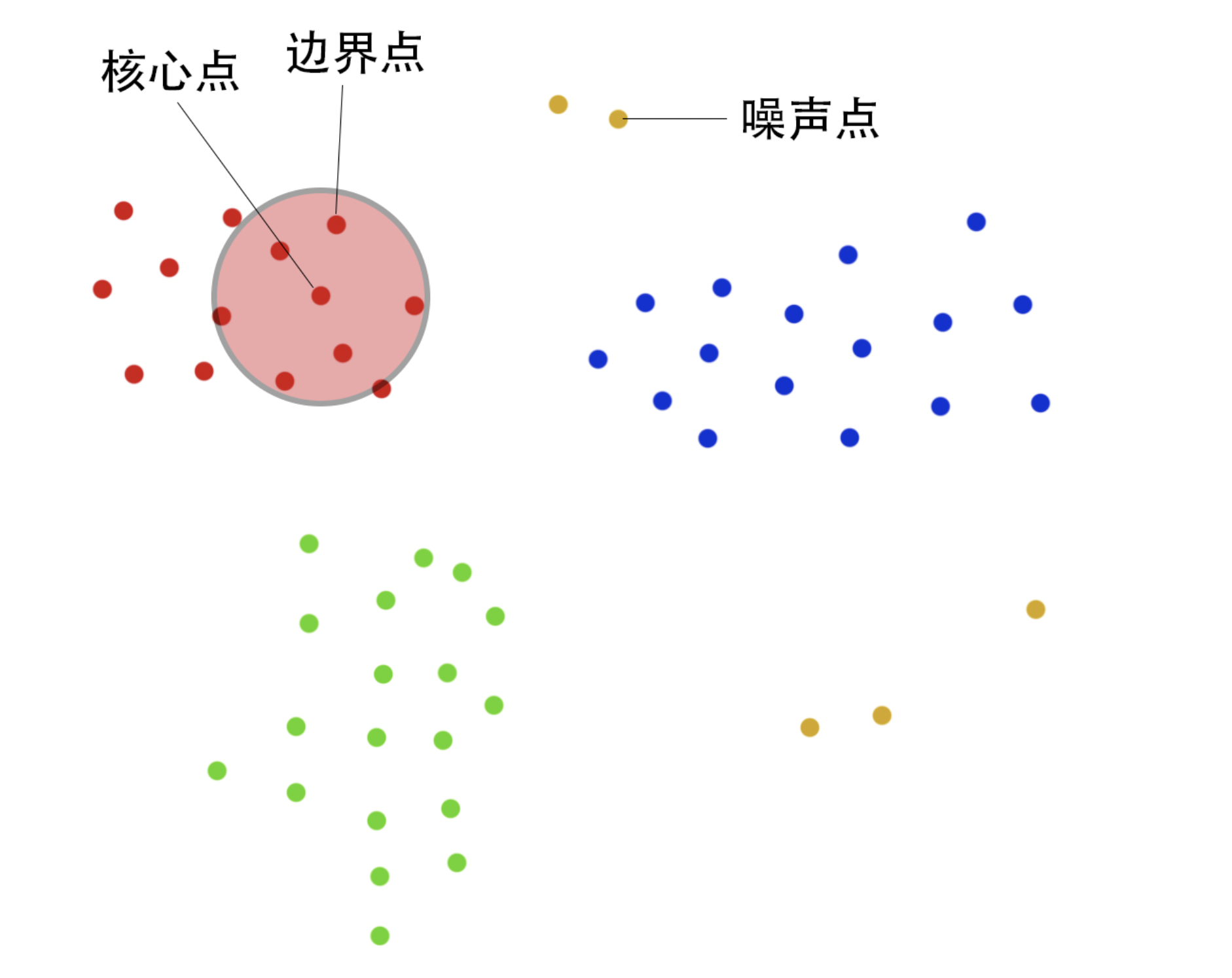
类别	说明
核心点	邻域半径 Eps 内样本点的数目 >= 最小点数目 minpoints 的点。
边界点	不属于核心点但在某个核心点的邻域内的点。
噪声点	既不是核心点也不是边界点。

2.4 点的关系

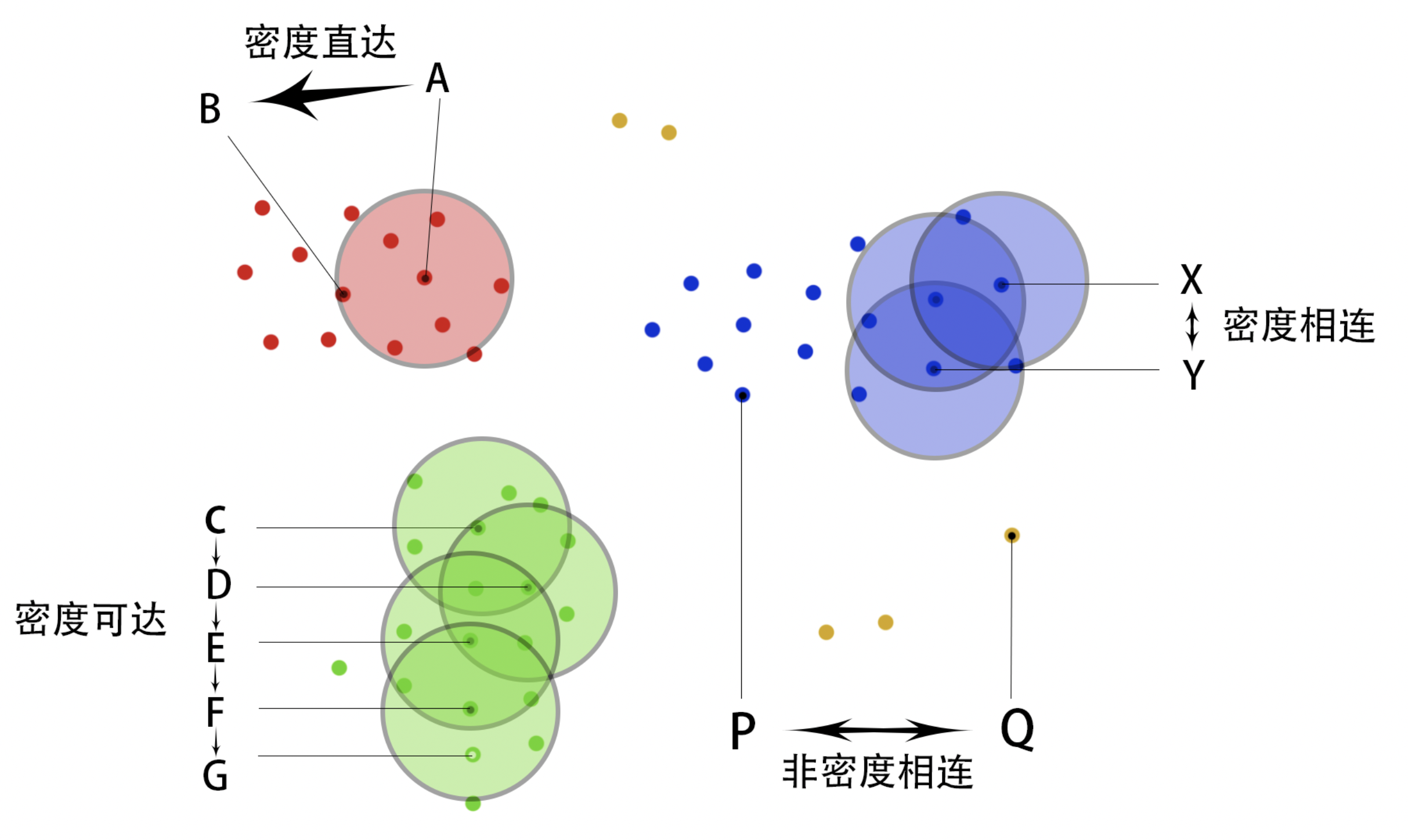
关系	说明
密度直达	A 为核心点，B 在 A 的邻域 Eps 内，那么 A 到 B 密度直达。任何核心点到其邻域 Eps 内的边界点都是密度直达。
密度可达	如果存在核心点 C、D、E、F。C 到 D 密度直达，D 到 F 密度直达，E 到 F 密度直达。那么我们可以称 C 到 F密度可达。而 F(核心点)到 G(边界点)也是密度直达，C 到 G 也是密度可达。
密度相连	如果存在核心点使得样本点 X 跟样本点 Y 都密度可达，那么我们称 X 与 Y 密度相连。
非密度相连	不属于密度相连的话就是非密度相连，非密度相连的两个点属于不同的蔟，或者其中为噪声点。

2.5 算法实现步骤

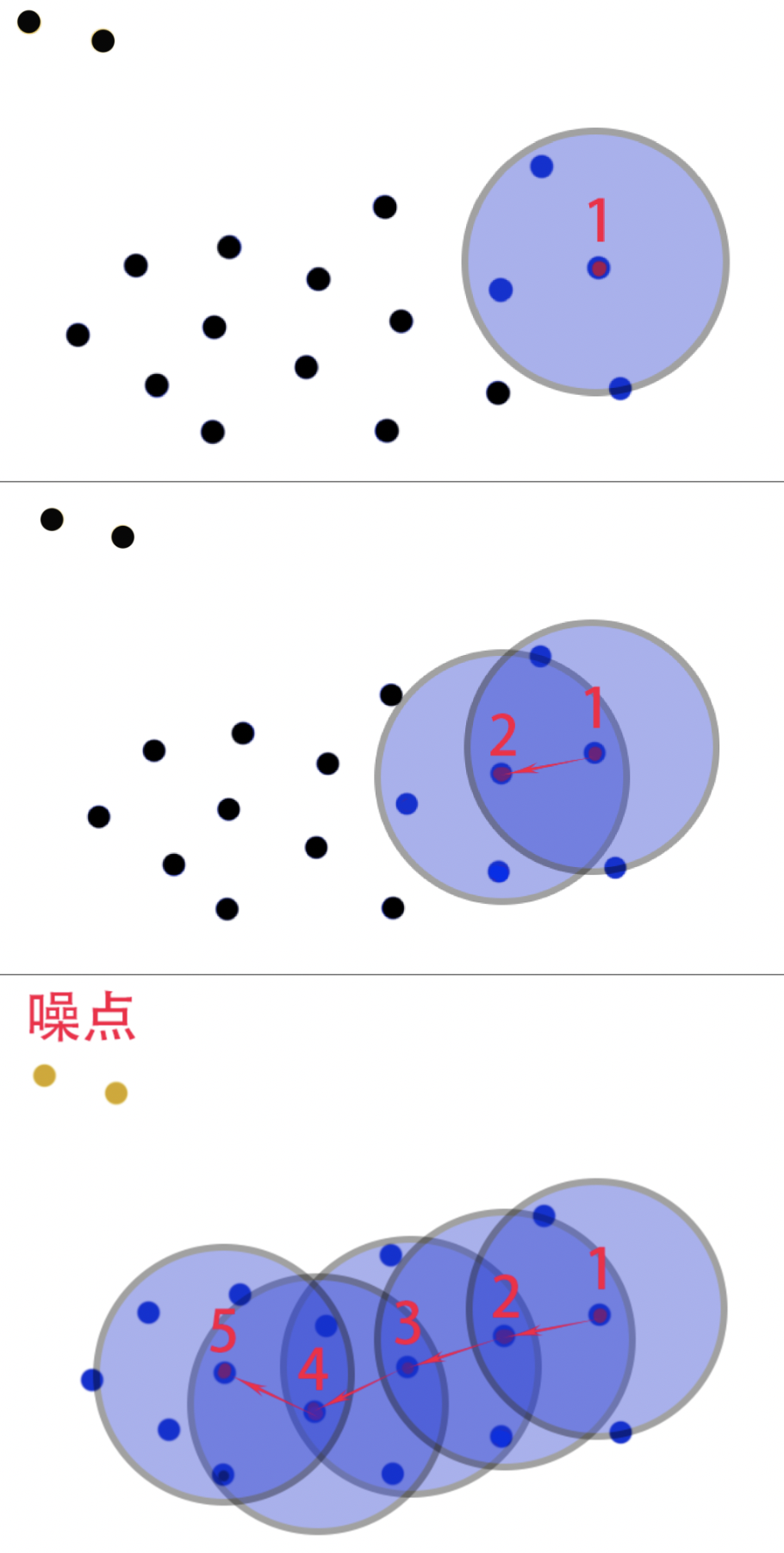
由密度可达关系导出的最大密度相连的样本集合，即为我们最终聚类的一个类别，或者说一个簇。在实现上我们可以分为以下 4 步：

步骤 1：选择任意一个没有类别的核心地点作为初始点；

步骤 2：找出这个核心点能够密度可达的样本集合，也就是找出这个核心点邻域内的所有边界点，这时就可以成为一个聚类蔟；

步骤 3：继续找另外一个没有类别的核心点继续重复步骤 2 的操作；

步骤 4：直到所有的点。

来点比较生动的例子：你可以假设一群人里面有个做传销的人（核心点），要发展下线，需要先找 N 个人（minPoints），于是他就在身边（邻域）去找人发展下线，那么下线（边界点）就会继续找下线，直到身边没人。

3 布局算法与 DBSCAN 的结合

简单介绍完 DBSCAN 的算法概念和算法实现后，我们讲一下聚类算法在 Deco 布局算法中的应用场景。

布局算法核心其实就是成组，如何基于设计稿每个模块的位置信息和大小尺寸来判断是否能组成成组是关键，简单来说，就是如何准确的把一堆节点拿个DIV套住。

如上图所示，设计稿上存在 11 个白色区块节点的节点，而我们肉眼去看，以每个节点之间的紧密距离关系来作为依据，上半部分和下半部分是分开的。但是这仅限于我们的视觉，那如何让机器的视觉也认为是分开的呢？我们需要刚刚提到的DBSCAN 聚类算法进行蔟的生成，那么我们的目标是让上半部分会形成一个聚类蔟，下半部分也组成一个聚类蔟。

刚刚我们提到 DBSCAN 是点到点之间的欧式距离作为紧密关系的依据，那么在节点上来看的话，我们转变下思路，改为 区块与区块之间的最短距离作为紧密关系的依据。

3.1 点状距离 > 区块距离

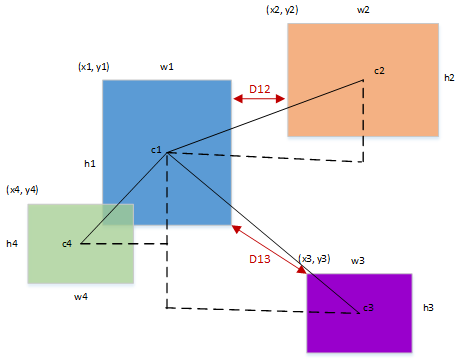
其实获取区块之间的最短距离比较简单，有三种情况：

第一种：两个区块相交，那么距离其实就是 0 了；

第二种：A 区块与 B 区块是在其上/下/左/右的，那么只需要获取两者之间的间距位置即可；

第三种：A 区块与 B 区块是在其左上/左下/右上/右下的，那么采用勾股定理获取下两者相对的顶点之间斜线的距离即可。

改造之后的效果就是下图的样子，我们根据聚类算法的实现，最终就可以把上下 2 个分成 2 个聚类蔟：

3.2 邻域半径推导

DBSCAN 聚类算法除了输入中，有样本数据集、数据对象数目阈值 MinPoints、邻域半径 Eps，那么带布局算法中，邻域半径 Eps到底设多少才是合适的值呢？总不能是个固定值吧。有些模块间距的整体大一点，有些间距小一点，我们在实际布局对区块做聚合的时候需要求出这个动态的邻域半径 Eps。

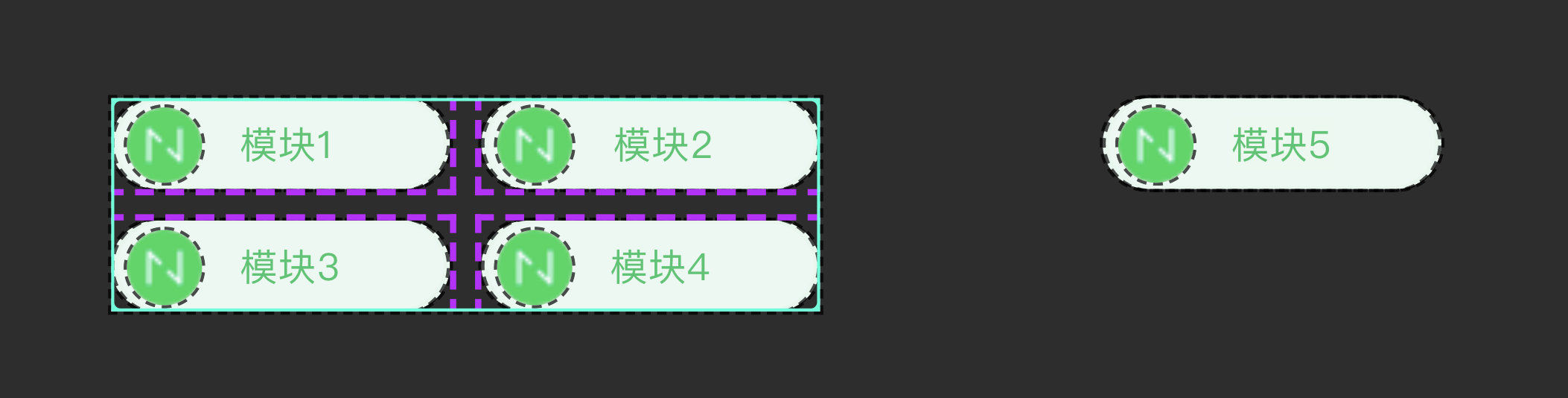
第一步：我们对样本数据集之间的距离先做一个统计，先求出这 5 个区块它们之间的最短距离：

	模块 1	模块 2	模块 3	模块 4	模块 5
模块 1	-	5	5	7	210
模块 2	5	-	7	5	100
模块 3	5	7	-	5	214
模块 4	7	5	5	-	107
模块 5	210	100	214	107	-

第二步：然后我们根据距离矩阵表，我们可以得出每个模块与其最相近模块之间的最短距离：

模块	模块 1	模块 2	模块 3	模块 4	模块 5
最短距离	5	5	5	5	100

第三步：在这堆数据中，我们需要提取占比更多，比较有效的数据作为我们的 Eps 值，剔除掉一些干扰项：

我们根据标准差的计算公式，我们取 1 倍标准差作为过滤项，筛选出符合多数样本的数据集，拿[5、5、5、5、100]求它的标准差，我们可以得出，总体标准偏差 38，平均值为 24。

那我们取一倍标准差作为依据，可以得出在一倍标准差的范围内，取数最大值为 24 + 38 = 62，那么我们就可以拿 62 作为我们在这个样本集的邻域半径 Eps。

3.3 算法优化

基于上述的算法改造，其实我们已经完成比较靠谱的在布局上实现模块聚类以及拆分。那么在实际算法的运用上，还会针对邻域半径 Eps 动态生成做一个在布局实际场景的优化：

比如像下面这种布局：水平间距为 5、垂直间距为 10：

那么如果根据最短距离标准差的形式，那其实 8 个模块它们的最短距离都是 5，最终算出来 Eps 也是 5，那么很有可能就会把上下两行分割开了。

所以我们在实际运用上，在生成标准差样本过程中，根据一定的规则，把水平距离的“10”也考虑进去，并作为标准差的样本进行计算。

4.技术落地

以上技术已经落地在 Deco 智能代码生成项目上，Deco 是我们团队在「前端智能化」方向上的探索，其聚焦设计稿一键生成多端代码这一切入点，实现将 Sketch/Photoshop 等设计稿进行解析并直接生成多端代码（Taro/React/Vue）的能力。Deco 可以使前端工程师不需要花大量精力关注设计稿，大大节约了开发成本，为输出更多的多端页面提供了有力的支持，也为业务降本增效带来了巨大动力。

在过去的一年里，Deco 已在京东的两次大促中成功落地，在个性化活动会场的搭建中，研发效率提升达到了 48%。

感兴趣的同学可以移步 Deco 官网进行体验。另外也给大家附上Deco体验的保姆级教程。

5.总结

本篇文章主要介绍了 DBSCAN 的实现原理，在介绍中并有给出具体的代码实现，这块大家感兴趣的话网上也有很多具体的代码实现逻辑。目的主要是给大家讲聚类算法的实现思路，以及在聚类算法在 D2C 上布局上的的应用落地。除了 DBSCAN 这种基于密度聚类算法外，其实还有很多算法也可在 D2C 布局算法上等待我们的挖掘。

引用文献：

[1] [DBSCAN 密度聚类算法] (https://www.cnblogs.com/pinard/p/6208966.html)
[2] [DBSCAN 聚类算法——机器学习（理论+图解+python 代码）] (https://blog.csdn.net/huacha__/article/details/81094891)
[3] [DBSCAN 详解] (https://blog.csdn.net/hansome_hong/article/details/107596543)

欢迎关注凹凸实验室博客：aotu.io

或者关注凹凸实验室公众号（AOTULabs），不定时推送文章：