Adversarial Examples Are Not Bugs, They Are Features

概
主要内容

Ilyas A, Santurkar S, Tsipras D, et al. Adversarial Examples Are Not Bugs, They Are Features[C]. neural information processing systems, 2019: 125-136.

@article{ilyas2019adversarial,

title={Adversarial Examples Are Not Bugs, They Are Features},

author={Ilyas, Andrew and Santurkar, Shibani and Tsipras, Dimitris and Engstrom, Logan and Tran, Brandon and Madry, Aleksander},

pages={125--136},

year={2019}}

概

作者认为, 标准训练方法, 由于既能学到稳定的特征和不稳定的特征, 而导致模型不稳定. 作者通过将数据集分解成稳定和非稳定数据来验证其猜想, 并利用高斯分布作为一特例举例.

主要内容

本文从二分类模型入手.

符号说明及部分定义

$(x,y) \in \mathcal{X} \times \{\pm 1\}$: 样本和标签;

$C:\mathcal{X} \rightarrow \{\pm 1\}$: 分类器;

$f:\mathcal{X} \rightarrow \mathbb{R}$ : 特征;

$\mathcal{F}=\{f\}$: 特征集合;

注: 假设$\mathbb{E}_{(x,y) \sim \mathcal{D}}[f(x)]=0$, $\mathbb{E}_{(x,y) \sim \mathcal{D}}[f(x)^2]=1$.

注: 在深度学习中, $C$可以理解为

\[C(x) = \mathrm{sgn} \big( b+ \sum_{f \in F_C} w_f \cdot f(x) \big ).
\]

$\rho$可用特征

满足

\[\tag{1}
\mathbb{E}_{(x,y) \sim \mathcal{D}}[y \cdot f(x)] \ge \rho >0,
\]

并记$\rho_{\mathcal{D}}(f)$为最大的$\rho$.

$\gamma$稳定可用特征

若$f$ $\rho$可用, 且对于给定的摄动集合$\Delta$

\[\tag{2}
\mathbb{E}_{(x, y) \sim \mathcal{D}} [\inf_{\delta \in \Delta(x)} y \cdot f(x+ \delta)] \ge \gamma > 0,
\]

则$f$ 为$\gamma$稳定可用特征.

可用不稳定特征

即对于$f$, $\rho_{\mathcal{D}}(f) >0$, 但是不存在$\gamma >0$使得(2)式满足.

标准(standard)训练

即最小化期望损失(在实际中为经验风险):

\[\tag{3}
\mathbb{E}_{(x,y) \sim \mathcal{D}} [\mathcal{L}_{\theta} (x, y)],
\]

$\mathcal{L}_{\theta}$的取法多样, 比如

\[\mathcal{L}_{\theta}(x, y) = - [y \cdot \big( b+ \sum_{f \in F_C} w_f \cdot f(x) \big )].
\]

稳定(robust)训练

\[\tag{4}
\mathbb{E}_{(x, y) \sim \mathcal{D}} [\max_{\delta \in \Delta(x)} \mathcal{L}_{\theta} (x+\delta, y)].
\]

分离出稳定数据

何为稳定数据? 即在此数据上, 利用标准的训练方式训练得到的模型能够在一定程度上免疫攻击. 如果能从普通的数据中分离出稳定数据和不稳定数据, 说明上面定义的稳定和非稳特征的存在性.

首先假设$C$是一个稳定模型(可通过PGD训练近似生成), 则$\hat{D}_{R}$应当满足

\[\tag{5}
\mathbb{E}_{(x, y) \sim \hat{D}_{R}}[f(x) \cdot y] =
\left \{
\begin{array}{ll}
\mathbb{E}_{(x, y) \sim D}[f(x) \cdot y] & if \: f \in F_C, \\
0 & otherwise.
\end{array} \right.
\]

为了满足第一条, 需要

\[\tag{6}
\min_{x_r} \quad \|g(x_r) - g(x)\|_2,
\]

其中$g$为将$x$映射到表示层(representation layer)的映射?

为了满足第二条, 在选择$x_r$的初始值的时候, 从$\mathcal{D}$中随机采样$x'$, 以保证$x'$和$y$没有关系, 则$\mathbb{E}_{(x, y) \sim D}[f(x') \cdot y] = \mathbb{E}_{(x, y) \sim D}[f(x')] \cdot \mathbb{E}_{(x, y) \sim D}[y] = 0$.

分离出不稳定数据

分离出不稳定数据所需要的是标准的模型$C$, 且

\[\tag{7}
x_{adv} = \arg \min_{\|x'-x\| \le \epsilon} L_C(x', t),
\]

其中$L_C$是认为给定的损失函数(比如:交叉熵), 而$t$是通过某种方式给定的标签, 且$C(x) = y$, $C(x')=t$.

既然摄动很小, 且$x_{adv}$的标签为$t$, 所以此时$F_C$中既有稳定特征, 又有不稳定特征.

$t$随机选取

此时稳定性特征和$t$不相关, 故其可用度应当为0, 而不稳定特征可用度大于0, 故

\[\tag{8}
\mathbb{E}_{(x, y) \sim \hat{D}_{rand}}[f(x) \cdot y]
\left \{
\begin{array}{ll}
.> 0 & if \: f \: non-robustly \: useful, \\
\approx 0 & otherwise.
\end{array} \right.
\]

$t$选取依赖于$y$

\[\tag{9}
\mathbb{E}_{(x, y) \sim \hat{D}_{det}}[f(x) \cdot y] =
\left \{
\begin{array}{ll}
.> 0 & if \: f \: non-robustly \: useful \\
< 0 & if \: f\: robustly \: useful \\
\in \mathbb{R} & otherwise.
\end{array} \right.
\]

比较重要的实验

1

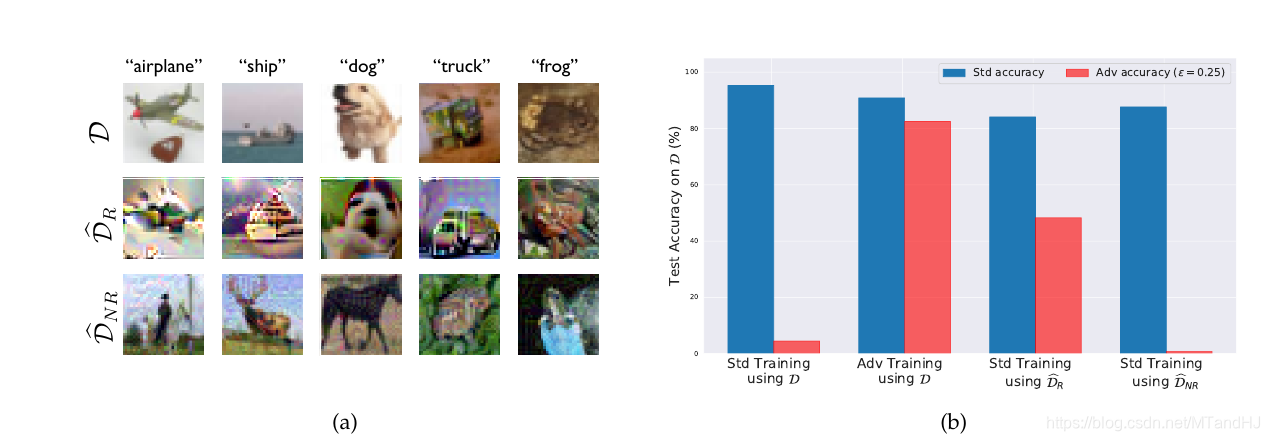
上面左图从上到下分别是标准数据, 稳定数据和不稳定数据, 右图进行了四组不同的实验:

在标准数据上标准训练并对其攻击
在标准数据上稳定训练并对其攻击
在稳定数据上标准训练并对其攻击
在不稳定数据上标准训练并对其攻击

不难发现, 在稳定数据上标准训练能够一定程度上免疫攻击, 而在不稳定数据上标准训练, 能够逼近在标准数据上标准训练的结果, 而其对攻击的免疫程度也正如我们所想的一塌糊涂.

这些实验可以说明, 稳定特征和不稳定特征是存在的, 标准训练由于最大限度地追求准确度, 所以其对二类特征一视同仁, 全盘接受, 这导致了不稳定.

迁移性

adversarial attacks的一个很明显的特征便是迁移性, 稳定特征和不稳定特征能够解释这一点, 既然数据相同, 不同结构的网络会从中提取出类似的不稳定特征.

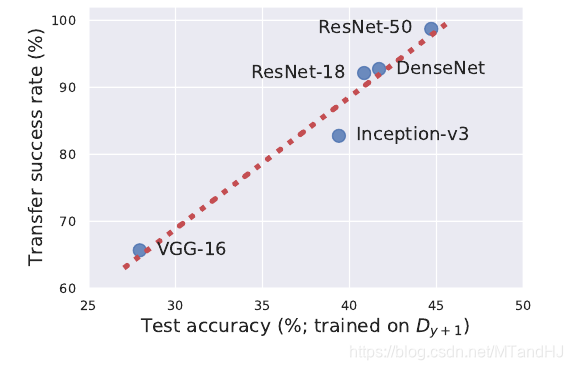
利用从ResNet-50中提取的不稳定数据, 提供给别的模型训练, 可以验证迁移性.

理论分析

作者通过一个正态分布的例子来告诉我们稳定特征和不稳定特征的存在和作用.

注: 下面涉及到的$\Sigma, \Sigma_*$均为对角阵.

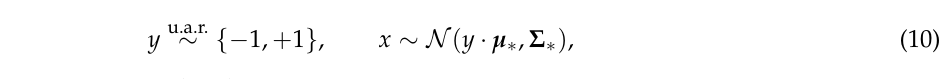
标准训练的目标是通过极大似然估计$\Theta=(\mu, \Sigma)$,

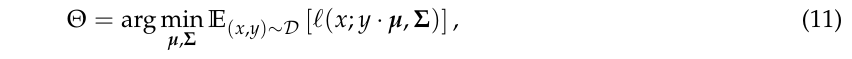
其中$\ell$为密度函数的$-\log$.

于是,

\[C(x)= \mathrm{sign}(x^T \Sigma^{-1} \mu).
\]

注: 无特别约束(11)的最优解即位$\mu_*, \Sigma_*$.

稳定训练的目标是

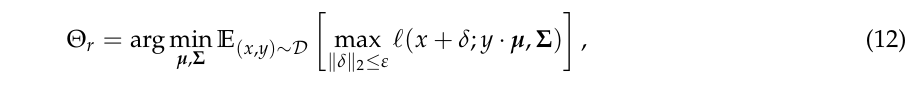
则有以下结论

定理1

注: $\mathcal{L}(\Theta)=\mathbb{E}_{(x, y) \sim \mathcal{D}}[\ell(x, y,\mu, \Sigma)]$, $\mathcal{L}_{adv}(\Theta)$的定义是类似的.

定理2

注意, 此时考虑的问题与上面的不同(定理3同定理2）, 为

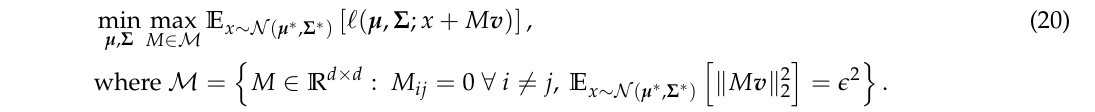
定理3

定理的证明, 这里不贴了, 其中有一个引理的证明很有趣.