CHARACTERIZING ADVERSARIAL SUBSPACES USING LOCAL INTRINSIC DIMENSIONALITY

概
主要内容
- LID
- LID估计
- 算法
- 实验
  - 1
- 2
- 3
- 4
- 5

Ma X, Li B, Wang Y, et al. Characterizing Adversarial Subspaces Using Local Intrinsic Dimensionality[J]. arXiv: Learning, 2018.

@article{ma2018characterizing,

title={Characterizing Adversarial Subspaces Using Local Intrinsic Dimensionality},

author={Ma, Xingjun and Li, Bo and Wang, Yisen and Erfani, Sarah M and Wijewickrema, Sudanthi and Houle, Michael E and Schoenebeck, Grant and Song, Dawn and Bailey, James},

journal={arXiv: Learning},

year={2018}}

概

本文介绍了一种local intrinsic dimensionality(LID)的指标用以揭示普通样本和对抗样本的本质区别, 这个指标可以用用来进行防御(即在样本进来的时候, 提前预判其是否是对抗样本).

主要内容

已有的一些用来区分普通样本和对抗样本的方法, 诸如KD(核密度估计) 和 BU(贝叶斯不确定度, 这个不是很了解), 但是其效果不明显, 本文提出的LID指标能够在各方面胜过他们.

比如在下图中, KM(k均值距离: 取样本$x$到最近的k个样本的距离的平均), 以及核密度估计(KD), 在普通样本和对抗样本上的指标是一致的, 此时无法判断, 而本文的LID的方法却能够判断(LID越大越偏离普通样本).

LID

由一个点为中心, 向外以超距体的方式发散, 其体积$V$与边长$r$的关系可知

\[\frac{V_2}{V_1} = (\frac{r_2}{r_1})^m \rightarrow m= \frac{\log (V_2/V_1)}{ \log (r_2 / r_1)},
\]

其中$m$为维度.

于是有人就想出把这种思想推广到一般的数据(数据的分布可能是一个低维的流形)

定义(LID): 给定样本$x \in \mathcal{X}$, 令$R >0$表示$x$到其它样本的距离的随机变量, 并用$F(r)$表示概率$P(R\le r)$, 且假设其关于$r>0$连续可微, 则在$x$点的距离为$r$的LID定义为

\[\tag{2}
\mathrm{LID}_F(r) := \lim_{\epsilon \rightarrow 0} \frac{\log (F((1+\epsilon)\cdot r) / F(r))}{\log (1+\epsilon)}=\frac{r\cdot F'(r)}{F(r)},
\]

若极限存在.

注: 最后一个等式成立, 只需中间式子上下同除以$\epsilon$再分别取极限即可(既然二者的极限都存在).

最后,

\[\tag{3}
\mathrm{LID}_F := \lim_{r \rightarrow 0} \mathrm{LID}_F(r).
\]

此即位我们最后要的LID($r \rightarrow 0$是因为我们关注的是局部信息).

LID估计

\[\tag{4}
\widehat{\mathrm{LID}}(x)= - (\frac{1}{k} \sum_{i=1}^k \log \frac{r_i(x)}{r_k(x)})^{-1}.
\]

算法

作者为了利用LID区分对抗样本, 训练了一个分类器. 在预先训练好的网络$H$上, 对每一个样本, 第i层的输出为$H^i(x)$, 对每一层的输出, 我们都计算其LID(这一步会用到别的训练数据)并保存下来. 利用这些提取出来的特征(LID), 训练二分类器(作者采用逻辑斯蒂回归).

实验

1

作者首先分析了, 普通样本(normal), 噪声样本(noisy), 对抗样本(adv)的LID指标, 可以发现，LID对对抗样本很敏感, 下面右图分析了在不同层中提取出来的LID值用于区分对抗样本的成功率.

2

比较了不同方法 KD, BU, KD+BU, LID在不同数据下, 对利用不同攻击方法生成的对抗样本进行区分的效果(途中的指标为AUC, AUC指标越大越好)

3

作者在FGM上计算LID并训练分类器, 再用别的方法生成对抗样本, 再测试效果.

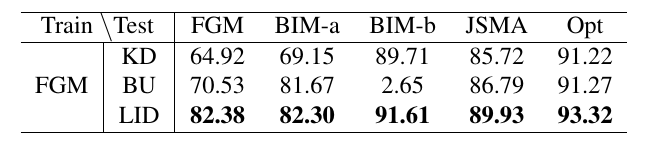
4

作者为了探究每一个batch的大小, 以及超参数$k$的影响, 做了实验, 显然batch size大一点比较好.

5

作者最小化下式生成对抗样本,

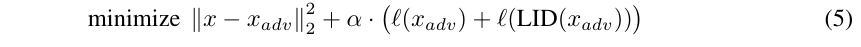
结果这些样本不能够欺骗过LID.

注: 已经别的文章指出, 其成功的原因在于破坏了梯度, 更改一下损失函数就能攻破.