poj 1039 Pipe（几何基础）

Pipe

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9932		Accepted: 3045

Description

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting.


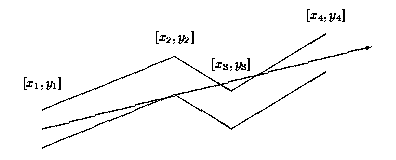
Each pipe component consists of many straight pipes connected
tightly together. For the programming purposes, the company developed
the description of each component as a sequence of points [x1; y1], [x2;
y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the
upper points of the pipe contour. The bottom points of the pipe contour
consist of points with y-coordinate decreased by 1. To each upper point
[xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture
above). The company wants to find, for each pipe component, the point
with maximal x-coordinate that the light will reach. The light is
emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1]
(endpoints are emitting light too). Assume that the light is not bent at
the pipe bent points and the bent points do not stop the light beam.

Input

The
input file contains several blocks each describing one pipe component.
Each block starts with the number of bent points 2 <= n <= 20 on
separate line. Each of the next n lines contains a pair of real values
xi, yi separated by space. The last block is denoted with n = 0.

Output

The
output file contains lines corresponding to blocks in input file. To
each block in the input file there is one line in the output file. Each
such line contains either a real value, written with precision of two
decimal places, or the message Through all the pipe.. The real value is
the desired maximal x-coordinate of the point where the light can reach
from the source for corresponding pipe component. If this value equals
to xn, then the message Through all the pipe. will appear in the output
file.

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

Source

Central Europe 1995

【思路】

线段直线相交。

如果一条直线没有经过两个拐点一定不是最优的直线，可以通过旋转移动使之更优。

枚举上线顶点，判断相交，求出交点。

【代码】

 #include<cmath>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int N = ;
 const double eps = 1e-;

 struct Pt{
     double x, y;
 }a[N], b[N];
 struct Line{ double a, b, c; };
 int n;
 double ans;

 double mult(Pt sp, Pt ep, Pt op){
     return (sp.x-op.x)*(ep.y-op.y) - (ep.x-op.x)*(sp.y-op.y);
 }
 Line getLine(Pt p1, Pt p2){
     Line ans;
     ans.a = p1.y - p2.y;
     ans.b = p2.x - p1.x;
     ans.c = p1.x*p2.y - p2.x*p1.y;
     return ans;
 }

 bool solve(Pt p1, Pt p2, int e){
     int i, flag;
     for(i = ; i < n-; i ++) {
         if(mult(p2, a[i], p1) < -eps || mult(p2, a[i+], p1) < -eps){
             flag = ; break;
         }
         if(mult(p2, b[i], p1) > eps || mult(p2, b[i+], p1) > eps){
             flag = ; break;
         }
     }
     if(i == n-) return true;   //  没有与任何的管道相交，Through all the pipe.
     if(i < e) return false;     //  光线不合法。
     Line l1, l2;                //  光线合法，求出射到的最远距离。
     l1 = getLine(p1, p2);
     if(flag == ) l2 = getLine(a[i], a[i+]);
     else l2 = getLine(b[i], b[i+]);
     ans = max(ans, (l1.b*l2.c-l2.b*l1.c)/(l1.a*l2.b-l2.a*l1.b));
     return false;
 }

 int main(){
     int i, j;
     while(scanf("%d", &n) && n){
         for(i = ; i < n; i ++){
             scanf("%lf%lf", &a[i].x, &a[i].y);
             b[i].x = a[i].x;
             b[i].y = a[i].y - ;
         }
         ans = -1e9;
         bool flag = ;
         if(n < ) flag = ;
         for(i = ; i < n; i ++) {
             for(j = i + ; j < n; j ++){
                 flag = solve(a[i], b[j], j);
                 if(flag) break;
                 flag = solve(b[i], a[j], j);
                 if(flag) break;
             }
             if(flag) break;
         }
         if(flag) puts("Through all the pipe.");
         else printf("%.2lf\n", ans);
     }
     return ;
 }