P1979 [NOIP]华容道

【问题描述】

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；
有些棋子是固定的，有些棋子则是可以移动的；
任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次

玩的时候，空白的格子在第 EXi 行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi列，目标位置为第 TXi 行第 TYi 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

输入输出格式

输入格式：

输入文件为 puzzle.in。

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出格式：

输出文件名为 puzzle.out。

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

输入输出样例

输入样例#1：复制

3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2

输出样例#1：复制

2
-1

说明

【输入输出样例说明】

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

移动过程如下：

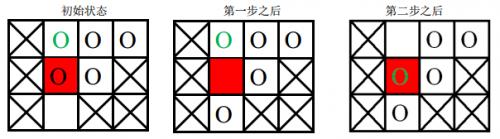
第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

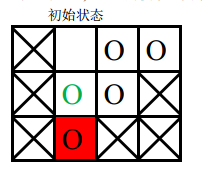
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2， 2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无

法完成。

【数据范围】

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1；

对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10；

对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

题解：

　　发现每个点需要移动时空格都需要在其四周，所以可以预处理出每个点到其四周的最少的步数，

　　然后每次输入时，处理处空格到其四周，现将空格移到起始点周围，然后每次交换位置，再移动，

　　这时就可以直接根据预处理的图进行最短路就ok了。

 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<cstdio>
 #include<iostream>
 #include<queue>
 #define fzy pair<int,int>
 #define inf 100000007
 using namespace std;
 
 const int lx[]={-,,,};
 const int ly[]={,,-,};//上为0，下为1，左为2，右为3 
 
 int n,m,q;
 int d[];bool ins[];
 int p[][],dis[][];
 int cnt,head[],next[],rea[],val[];
 
 void add(int u,int v,int fee)
 {
     next[++cnt]=head[u];
     head[u]=cnt;
     rea[cnt]=v;
     val[cnt]=fee;
 }
 void bfs(int sx,int sy,int bx,int by,int flag)//sx,sy表示空格位置，bx，by表示目标棋子位置。
 {
     queue<fzy>q;
     while(!q.empty()) q.pop();
     q.push(make_pair(sx,sy));
     memset(dis,,sizeof(dis));//用来处理不经过目标点到达其身边。
     dis[sx][sy]=;
     while(!q.empty())
     {
         int nx=q.front().first,ny=q.front().second;q.pop();
         for (int i=;i<;i++)
         {
             int tx=nx+lx[i],ty=ny+ly[i];
             if (p[tx][ty]&&!dis[tx][ty]&&(tx!=bx||ty!=by))//可以走，未到过，不是目标点。
             {
                 dis[tx][ty]=dis[nx][ny]+;
                 q.push(make_pair(tx,ty));
             }
         }
     }
     if (flag>) return;
     for (int i=;i<;i++)
     {
         int tx=bx+lx[i],ty=by+ly[i];
         if ((tx!=sx||ty!=sy)&&dis[tx][ty]) add(bx*+by*+flag,bx*+by*+i,dis[tx][ty]-);//表示不经过目标点到达其身边。
     }
     add(bx*+by*+flag,sx*+sy*+flag^,);//表示直接交换。
 }
 void solve_spfa(int bx,int by)
 {
     queue<int>q;
     while(!q.empty()) q.pop();
     for (int i=;i<;i++)
         d[i]=inf,ins[i]=;
     for (int i=;i<;i++)
     {
         int tx=bx+lx[i],ty=by+ly[i],tn=bx*+by*+i;
         if (dis[tx][ty])
         {
             d[tn]=dis[tx][ty]-;
             q.push(tn);
             ins[tn]=;
         }
     }
     while(!q.empty())
     {
         int now=q.front();q.pop();
         for (int i=head[now];i!=-;i=next[i])
         {
             int v=rea[i],fee=val[i];
             if(d[now]+fee<d[v])
             {
                 d[v]=d[now]+fee;
                 if (!ins[v])
                 {
                     ins[v]=;
                     q.push(v);
                 }
             }
         }
         ins[now]=;
     }
  }
 int main()
 {
     scanf("%d%d%d",&n,&m,&q);
     memset(head,-,sizeof(head));
     for (int i=;i<=n;i++)
         for (int j=;j<=m;j++)
             scanf("%d",&p[i][j]);
     for (int i=;i<=n;i++)
         for (int j=;j<=m;j++)
         {
             if (!p[i][j]) continue;
             if (p[i-][j]) bfs(i-,j,i,j,);
             if (p[i+][j]) bfs(i+,j,i,j,);
             if (p[i][j-]) bfs(i,j-,i,j,);
             if (p[i][j+]) bfs(i,j+,i,j,);
         }
     while(q--)
     {
         int sx,sy,bx,by,mx,my;
         scanf("%d%d%d%d%d%d",&sx,&sy,&bx,&by,&mx,&my);
         if (bx==mx&&by==my)
         {
             puts("");
             continue;
         }
         bfs(sx,sy,bx,by,);
         solve_spfa(bx,by);
         int ans=inf;
         for (int i=;i<;i++)
             ans=min(ans,d[mx*+my*+i]);
         if (ans<inf) printf("%d\n",ans);
         else puts("-1");
     }
 }