[Luogu] P4198 楼房重建

题目描述

小A的楼房外有一大片施工工地，工地上有N栋待建的楼房。每天，这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆，数自己能够看到多少栋房子。

为了简化问题，我们考虑这些事件发生在一个二维平面上。小A在平面上(0,0)点的位置，第i栋楼房可以用一条连接(i,0)和(i,Hi)的线段表示，其中Hi为第i栋楼房的高度。如果这栋楼房上任何一个高度大于0的点与(0,0)的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。

施工队的建造总共进行了M天。初始时，所有楼房都还没有开始建造，它们的高度均为0。在第i天，建筑队将会将横坐标为Xi的房屋的高度变为Yi(高度可以比原来大—修建，也可以比原来小—拆除，甚至可以保持不变—建筑队这天什么事也没做)。请你帮小A数数每天在建筑队完工之后，他能看到多少栋楼房？

输入输出格式

输入格式：

第一行两个正整数N,M

接下来M行，每行两个正整数Xi,Yi

输出格式：

M行，第i行一个整数表示第i天过后小A能看到的楼房有多少栋

输入输出样例

输入样例#1：

3 4
2 4
3 6
1 1000000000
1 1

输出样例#1：

1
1
1
2

说明

对于所有的数据1<=Xi<=N，1<=Yi<=10^9

N,M<=100000

解题思路

首先看题面，对于每个位置，能不能被看到只取决于这个位置上楼的高度。换言之，取决于斜率k，（y = k x + b）。

暴力思路

求出每个点的斜率，然后循环扫一遍。

int max_k = -INF;
for(int i = ; i <= n; i++) {
    if(k[i] > max_k) {
        max_k = k[i];
        ans++;
    }
}

加上内存优化后实测50分。

优化

在暴力思路中，我们每次在找的只是最值。
根据公式：

区间 + 最值 = 线段树

可以考虑使用线段树优化。

具体办法是：

利用线段树维护每个区间的最大斜率以及能被看见的个数。

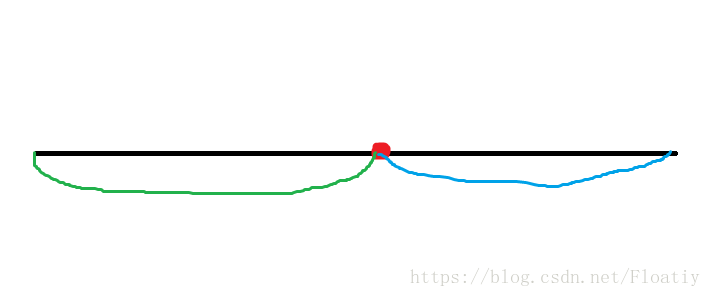
假设修改在图中红点处，那么绿色区能被看见的楼房不受影响，不需要改变。
对于蓝色区，如果最大斜率小于红点处的斜率，就全部去死吧把这个区间的能被看到的楼房数修改成0。else，往下递归。

重复执行：如果区间最大斜率小于红点斜率，区间数量就改成0，不然就接着递归，最后留下的就是能被看见的。

这样就可以水进时限了