light oj 1336 sigma function

常用的化简方法（高中就常用了）:     p^(e+1)-1/p-1=             [ p^(e+1) -p + (p-1) ]/ (p-1) = p*(p^e-1)/(p-1) + 1   （也可以直接分解p^e-1）

常用的思路：反面验证  比如本题，求偶数（试探后发现不太好求），则推出奇数条件

再看本题。要想让σ(n)为偶数，只要有一项为偶数即可，

化简变为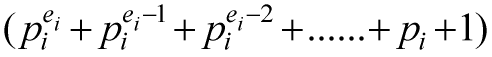，观察这个式子，pi都是素数，除2以外都是奇数，所以式子奇偶决定于ei，若ei为奇数，就相当于奇数个奇数（若pi不是2，那么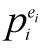肯定是奇数）相加，再加上1，偶数，反之，若ei为偶数，就是奇数。如果pi刚好是2，是奇数

得出结论：对于n，若将n进行唯一分解之后，如果存在任何一个 pi != 2 且 ei ( 1 <= i <= k )为奇数则 σ(n) 为偶数。

现在需要求的是计算1-n之间能让σ(k)为偶数的k的个数。有些复杂，所以考虑这个问题的反面，求1-n之间能让σ(k)为奇数的k的个数

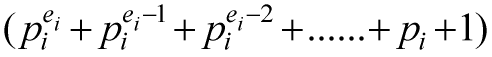若σ(n)为奇数，则每一项都必须为奇数，意味着每一项约分之后的都必须为奇数，也就是说每一项的ei都必须是偶数，也就是说n必须为平方数。但是前面证明过当pi为2时，无论ei是什么，这一项都是奇数，然而这些平方数乘以2之后，其σ仍是奇数（如果再乘以2，就是另一个平方数了，所以只需要考虑乘一个2），仍然符合条件。

所以n为平方数，或为平方数的2倍，那么σ(n)为奇数。而小于n的平方数为sqrt(n)个，这些平方数的2倍的个数是sqrt(n/2)。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
int main()
{
    int T;
    scanf("%d", &T);
    for(int kase = ; kase <= T; kase++)
    {
        ll n, sum;
        scanf("%lld", &n);
        sum = n;
        sum -= (int)sqrt(n);
        sum -= (int)sqrt(n/);
        printf("Case %d: %lld\n", kase, sum);
    }
    return ;
}