Codeforces 768 E. Game of Stones 博弈DP

E. Game of Stones

 

Sam has been teaching Jon the Game of Stones to sharpen his mind and help him devise a strategy to fight the white walkers. The rules of this game are quite simple:

• The game starts with n piles of stones indexed from 1 to n. The i-th pile contains si stones.
• The players make their moves alternatively. A move is considered as removal of some number of stones from a pile. Removal of 0stones does not count as a move.
• The player who is unable to make a move loses.

Now Jon believes that he is ready for battle, but Sam does not think so. To prove his argument, Sam suggested that they play a modified version of the game.

In this modified version, no move can be made more than once on a pile. For example, if 4 stones are removed from a pile, 4 stones cannot be removed from that pile again.

Sam sets up the game and makes the first move. Jon believes that Sam is just trying to prevent him from going to battle. Jon wants to know if he can win if both play optimally.

Input

 

First line consists of a single integer n (1 ≤ n ≤ 106) — the number of piles.

Each of next n lines contains an integer si (1 ≤ si ≤ 60) — the number of stones in i-th pile.

Output

Print a single line containing "YES" (without quotes) if Jon wins, otherwise print "NO" (without quotes)

Examples

input

1
5

output

NO

Note

In the first case, Sam removes all the stones and Jon loses.

In second case, the following moves are possible by Sam: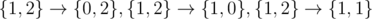 

In each of these cases, last move can be made by Jon to win the game as follows: 

 题意：

　　一堆石子，一开始你可以拿走任意个，假设拿走k(k>=1)个，那么另外一个人就不能再拿k个了

　　现在有n堆石子，两人轮流拿，不能拿的时候那个人就输了

问后手是否能赢

题解：

　　石子最多60颗，1<<60，状态压缩跑sg函数

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<LL,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18;
const double Pi = acos(-1.0);
const int N = 1e6+, maxn = 1e3+, mod = 1e9+, inf = 2e9;

map<LL,int > dp[N];
int sg[N],n;
int dfs(int x,LL dep) {
    if(dp[x].count(dep)) return dp[x][dep];
    LL ret = ;
    for(int i = ; i < x; ++i) {
        if(((dep>>i)&) == ) {
            ret |= <<(dfs(x-i-,dep|(<<i)));
        }
    }
    for(int i = ; i < ; ++i) {
        if((ret>>i&) == ) {
            dp[x][dep] = i;
            break;
        }
    }
    return dp[x][dep];
}
int main() {
    for(int i = ; i <= ; ++i) sg[i] = dfs(i,);
    scanf("%d",&n);
    int ans = ;
    for(int i = ; i <= n; ++i) {
        int x;
        scanf("%d",&x);
        ans ^= sg[x];
    }
    if(!ans) puts("YES");
    else puts("NO");
    return ;
}