【模式识别与机器学习】——3.5Fisher线性判别

---恢复内容开始---

出发点

　　应用统计方法解决模式识别问题时，一再碰到的问题之一就是维数问题。 在低维空间里解析上或计算上行得通的方法，在高维空间里往往行不通。 因此，降低维数有时就会成为处理实际问题的关键。

问题描述

考虑把d维空间的样本投影到一条直线上，形成一维空间，即把维数压缩到一维。

然而，即使样本在d维空间里形成若干紧凑的互相分得开的集群，当把它们投影到一条直线上时，也可能会是几类样本混在一起而变得无法识别。

但是，在一般情况下，总可以找到某个方向，使在这个方向的直线上，样本的投影能分得开。

问题：如何根据实际情况找到一条最好的、最易于分类的投影线，这就是Fisher判别方法所要解决的基本问题。

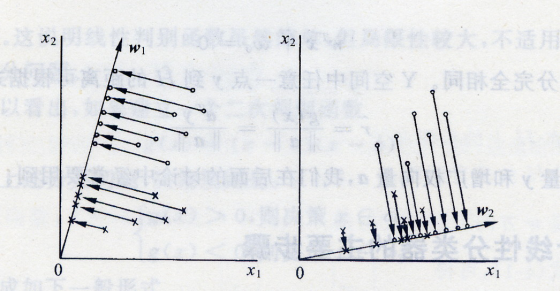
从d维空间到一维空间的一般数学变换方法

Fisher准则函数的定义

（1）几个必要的基本参量

　　我们希望投影后，在一维Y空间中各类样本尽可能分得开些，即希望两类均值之差越大越好，同时希望各类样本内部尽量密集，即希望类内离散度越小越好。

（2）Fisher准则函数

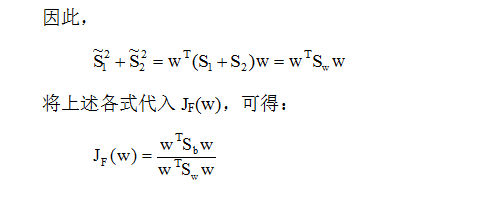
（3）最佳变换向量W*的求取

先修知识：Lagrange乘数法

最佳变换向量的求取

基于最佳变换向量w*的投影

　　w*是使Fisher准则函数JF(w)取极大值时的解，也就是d维X空间到一维Y空间的最佳投影方向。有了w*，就可以把d维样本x投影到一维，这实际上是多维空间到一维空间的一种映射，这个一维空间的方向w*相对于Fisher准则函数JF(w)是最好的。 利用Fisher准则，就可以将d维分类问题转化为一维分类问题，然后，只要确定一个阈值T，将投影点yn与T相比较，即可进行分类判别。