【算法•日更•第五十期】二分图（km算法）

▎前言

　　戳开这个链接看看，惊不惊喜，意不意外？传送门。

　　没想到我的博客竟然被别人据为己有了，还没办法投诉。

　　这年头写个博客太难了~~~

---

　　之前小编写过了二分图的一些基础知识和匈牙利算法，今天来讲一讲km算法，若你不知道匈牙利算法，请先看下面的博客。（否则会体验极差）

　　传送门

▎km算法

☞『引入』

　　之前学习的匈牙利算法还记得吗？它处理的是无权二分图，长这个样子：

　　

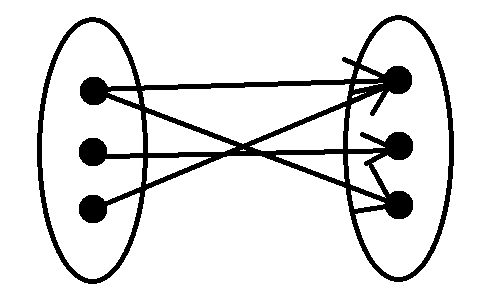
　　//mspaint画出来的真粗糙

　　但是如果加入了权值呢？比如说是这个样子的：

　　

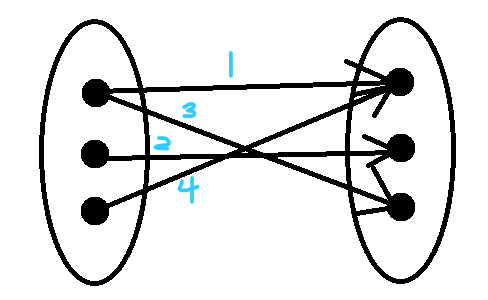
　　现在，我们的问题变了，不再求最大匹配问题了，而是最优匹配问题，就是说在原来的基础上，要求匹配值的和最大。

　　考虑使用匈牙利算法求解，显然，我们可以求出每一个最大匹配，然后比较权值和，但是当数据规模大起来后，这无疑是很暴力的，所以我们只能另起炉灶，使用km算法。

　　也就是说km算法是来处理有权二分图的。

☞『定义』

　　KM算法是一种计算机算法，功能是求完备匹配下的最大权匹配。在一个二分图内，左顶点为X，右顶点为Y，现对于每组左右连接XiYj有权wij，求一种匹配使得所有wij的和最大。（copy自百度百科）

☞『算法流程』

　　先来讲讲算法的原理吧，我们有这样一个图用来匹配：

　　

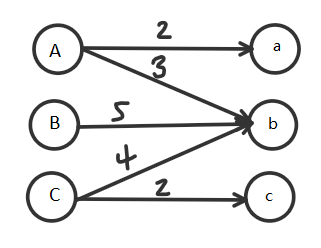
　　对于左边每个点我们设置一个量用来存对右边的所有边的权值的最大值。

　　对于右边的每个点我们设置一个量来存对左边点的需要程度。

　　从始至终，我们一直要对一个取的边保持一个式子：左边的取值最大值+右边的需求值=边的权值。

　　因此，右边初始需求值都为0。

　　那么，这个图，就长这个德性了：

　　

☞『算法模拟』

　　首先从第一条边开始寻找，不断试探，因为3+0=3直接使用最大的那条边（A -> b）：

　　

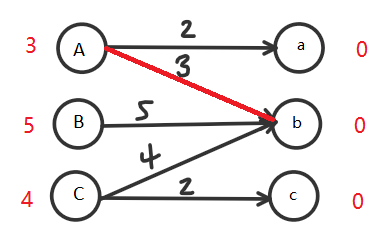
　　接着第二条5+0=5（B -> b）：

　　

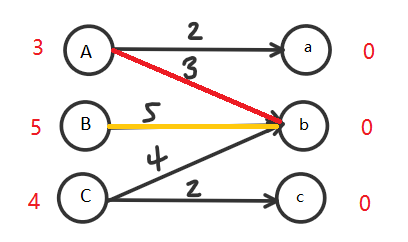
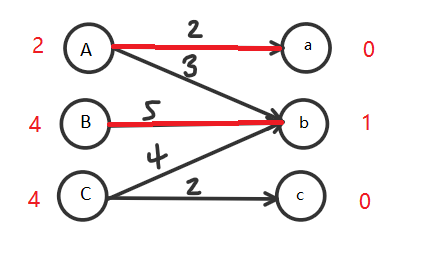
　　发生冲突！！！此时，要么A放弃，要么B放弃，两者皆可，不过B只有一条路走，所以我们放弃A，改选A -> a这条路：

　　

　　这个时候A所使用的不能是3了，而是2，所以修改A左边的数字为2，B也要减一，本图因为B只有一条路，所以B不能放弃，但是要记得正常情况下，两条边都可以放弃的，为了保证正常，我们应该修改b右边的值为1，使式子成立。

　　修改后就是这个样子的：

　　

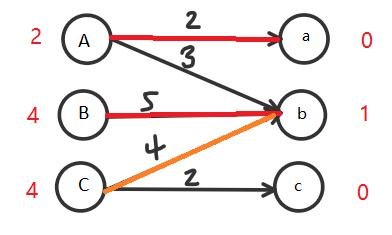
　　接着试探4，发现4+1！=4，（与B发生冲突）所以行不通：

　　

　　降低最大值走另一条路：

　　

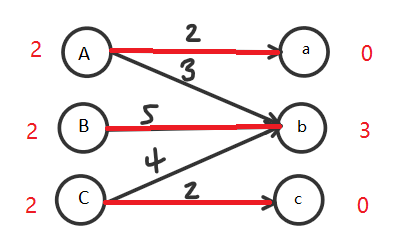
　　至此，算法演示结束。