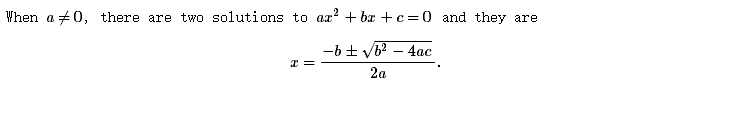【转载】markdown数学常用公式箭头符号

来源1：https://www.jianshu.com/p/3f01c5658356

来源2：https://blog.csdn.net/smstong/article/details/44340637

排版

行内与独行

名称	符号	示例语法	示例
行内公式	$公式内容$	$xyz$
公式内换行	\\	$$1+1=2 \\ 2+2=4$$

上标、下标与组合

名称	符号	示例语法	示例
上标符号	^	$x^4$
下标符号	_	$x_1$
组合符号	{}	$ a^2_{xyz}$

汉字、字体与格式

名称	符号	示例语法	示例
汉字形式	\mbox{}	$V_{\mbox{初始}}$
字体控制	\displaystyle	$\displaystyle \frac{x+y}{y+z}$
下划线符号	\underline	$\underline{x+y}$
标签	\tag{数字}	$\tag{11}$
上大括号	\overbrace{算式}	$\overbrace{a+b+c+d}^{2.0}$
下大括号	\underbrace{算式}	$a+\underbrace{b+c}_{1.0}+d$
上位符号	\stacrel{上位符号}{基位符号}	$\vec{x}\stackrel{\mathrm{def}}{=}{x_1,\dots,x_n}$

占位符

名称	符号	示例语法	示例
空格	\quad	$x \quad y$
两个空格	\qquad	$x \qquad y$
小空格	\,	$x \, y$
中空格	\;	$x \; y$
紧贴	\!	$x \! y$

定界符与组合

名称	符号	示例语法	示例
括号	()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg)	$()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg)$
中括号	[]	$[x+y]$
大括号	{ }	${x+y}$
自适应括号	\left \right	$\left(x\right), \left(x{yz}\right)$
组合公式	{上位公式 \choose 下位公式}	${n+1 \choose k}={n \choose k}+{n \choose k-1}$
组合公式	{上位公式 \atop 下位公式}	$\sum_{k_0,k_1,\ldots>0 \atop k_0+k_1+\cdots=n}A_{k_0}A_{k_1}\cdots$

运算

四则运算

名称	符号	示例语法	示例
加法运算	+	$x+y=z$
减法运算	-	$x-y=z$
加减运算	\pm	$x \pm y=z$
减加运算	\mp	$x \mp y=z$
乘法运算	\times	$x \times y=z$
点乘运算	\cdot	$x \cdot y=z$
星乘运算	\ast	$x \ast y=z$
除法运算	\div	$x \div y=z$
斜法运算	/	$x/y=z$
分式表示	\frac{分子}{分母}	$\frac{x+y}{y+z}$
分式表示	{分子} \voer {分母}	${x+y} \over {y+z}$
绝对值表示	||	$|x+y|$

高级运算

名称	符号	示例语法	示例
平均数运算	\overline{算式}	$\overline{xyz}$
开二次方运算	\sqrt	$\sqrt x$
开方运算	\sqrt[开方数]{被开方数}	$\sqrt[3]{x+y}$
对数运算	\log	$\log(x)$
极限运算	\lim	$\lim^{x \to \infty}_{y \to 0} {\frac{x}{y}}$
极限运算	\displaystyle \lim	$\displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$
求和运算	\sum	$\sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$
求和运算	\displaystyle \sum	$\displaystyle \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$
积分运算	\int	$\int^{\infty}_{0}{xdx}$
积分运算	\displaystyle \int	$\displaystyle \int^{\infty}_{0}{xdx}$
微分运算	\partial	$\frac{\partial x}{\partial y}$

逻辑运算

名称	符号	示例语法	示例
等于运算	=	$x+y=z$
大于运算	>	$x+y>z$
小于运算	<	$x+y<z$
大于等于运算	\geq	$x+y \geq z$
小于等于运算	\leq	$x+y \leq z$
不等于运算	\neq	$x+y \neq z$
不大于等于运算	\ngeq	$x+y \ngeq z$
不大于等于运算	\not\geq	$x+y \not\geq z$
不小于等于运算	\nleq	$x+y \nleq z$
不小于等于运算	\not\leq	$x+y \not\leq z$
约等于运算	\approx	$x+y \approx z$
恒定等于运算	\equiv	$x+y \equiv z$

集合运算

名称	符号	示例语法	示例
属于运算	\in	$x \in y$
不属于运算	\notin	$x \notin y$
不属于运算	\not\in	$x \not\in y$
子集运算	\subset	$x \subset y$
子集运算	\supset	$x \supset y$
真子集运算	\subseteq	$x \subseteq y$
非真子集运算	\subsetneq	$x \subsetneq y$
真子集运算	\supseteq	$x \supseteq y$
非真子集运算	\supsetneq	$x \supsetneq y$
非子集运算	\not\subset	$x \not\subset y$
非子集运算	\not\supset	$x \not\supset y$
并集运算	\cup		$x \cup y$
交集运算	\cap		$x \cap y$
差集运算	\setminus	$x \setminus y$
同或运算	\bigodot	$x \bigodot y$
同与运算	\bigotimes	$x \bigotimes y$
实数集合	\mathbb{R}	$\mathbb{R}$
自然数集合	\mathbb{Z}	$\mathbb{Z}$
空集	\emptyset	$\emptyset$

数学符号

名称	符号	示例语法	示例
无穷	\infty	$\infty$
虚数	\imath	$\imath$
虚数	\jmath	$\jmath$
数学符号	\hat{a}	$\hat{a}$
数学符号	\check{a}	$\check{a}$
数学符号	\breve{a}	$\breve{a}$
数学符号	\tilde{a}	$\tilde{a}$
数学符号	\bar{a}	$\bar{a}$
矢量符号	\vec{a}	$\vec{a}$
数学符号	\acute{a}	$\acute{a}$
数学符号	\grave{a}	$\grave{a}$
数学符号	\mathring{a}	$\mathring{a}$
一阶导数符号	\dot{a}	$\dot{a}$
二阶导数符号	\ddot{a}	$\ddot{a}$
上箭头	\uparrow	$\uparrow$
上箭头	\Uparrow	$\Uparrow$
下箭头	\downarrow	$\downarrow$
下箭头	\Downarrow	$\Downarrow$
左箭头	\leftarrow	$\leftarrow$
左箭头	\Leftarrow	$\Leftarrow$
右箭头	\rightarrow	$\rightarrow$
右箭头	\Rightarrow	$\Rightarrow$
底端对齐的省略号	\ldots	$1,2,\ldots,n$
中线对齐的省略号	\cdots	$x_1^2 + x_2^2 + \cdots + x_n^2$
竖直对齐的省略号	\vdots	$\vdots$
斜对齐的省略号	\ddots	$\ddots$

高级表示形式

矩阵

名称	符号	示例语法	示例
矩阵	\begin{matrix} 矩阵内容 \end{matrix}	$$ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix}$$
[]矩阵	\left[ \begin{matrix} 矩阵内容 \end{matrix} \right]	$$\left [ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] $$`
[]矩阵	\begin{bmatrix} 矩阵内容 \end{bmatrix}	$$ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} $$
{}矩阵	\begin{Bmatrix} 矩阵内容 \end{Bmatrix}	$$ \begin{Bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{Bmatrix} $$

希腊字母

字母	实现	字母	实现
A	A	α	\alhpa
B	B	β	\beta
Γ	\Gamma	γ	\gamma
Δ	\Delta	δ	\delta
E	E	ϵ	\epsilon
Z	Z	ζ	\zeta
H	H	η	\eta
Θ	\Theta	θ	\theta
I	I	ι	\iota
K	K	κ	\kappa
Λ	\Lambda	λ	\lambda
M	M	μ	\mu
N	N	ν	\nu
Ξ	\Xi	ξ	\xi
O	O	ο	\omicron
Π	\Pi	π	\pi
P	P	ρ	\rho
Σ	\Sigma	σ	\sigma
T	T	τ	\tau
Υ	\Upsilon	υ	\upsilon
Φ	\Phi	ϕ	\phi
X	X	χ	\chi
Ψ	\Psi	ψ	\psi
Ω	\v	ω	\omega

---

References

1. Markdown数学公式语法
2. 使用Markdown写矩阵、表格和一些数学公式(实用)

输入数学公式

• 输入数学公式
  • 数学公式的web解决方案
  • MathJax渲染过程简单模拟
    • 1 MathJax最简示例
    • 2 模拟MathJax渲染原理
  • CSDN-MarkDown编辑器常用数学公式输入教程
    • 1 公式定界符与关键字
    • 2 上下标
    • 3 括号和分隔符
    • 4 分数
    • 5 开方
    • 6 省略号
    • 7 矢量
    • 8 积分
    • 9 极限
    • 10 累加累乘
    • 11 希腊字母
    • 12 数学符号大汇总
    • 13 需要转义的字符
    • 14 使用指定字体

1 数学公式的web解决方案

在网页上显示漂亮的数学公式，是多年来数学工作者和学者的愿望。最容易实现的方式就是使用离线编辑器如word，Latex等编写完公式，然后截图作为图片在html网页中显示。然而这种方式存在很多缺点：

• 无法在线修改，离线修改后必须重新截图
• 放大显示会失真，这是位图的天生缺陷
• 不同的离线编辑器生成的显示效果不同，很难统一
• 由于无法直接编辑，所以即使看到了公式，也无法在此基础上进一步修改，不利于交流

当然，位图显示公式也有一个最大的优点，那就是兼容所有浏览器，不需要任何插件就可以浏览。

随着html, css的持续发展，使用纯html+css来显示公式已经非常可行，于是大名鼎鼎的MathJax出现了。它是一个开源的JavaScript库，用来把特定格式的公式描述转换为html+css或者svg代码，从而在浏览器上显示数学公式。

2 MathJax渲染过程简单模拟

2.1 MathJax最简示例

先来看一个带公式的最简网页实例mathjax.html。

<!DOCTYPE html>
<html>
    <head>
        <title>MathJax TeX Test Page</title>
        <script type="text/x-mathjax-config">
            MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]}});
        </script>
        <script type="text/javascript"
            src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML">
            </script>
        </head>
        <body>
            When $a \ne 0$, there are two solutions to \(ax^2 + bx + c = 0\) and they are
            $$x = {-b \pm \sqrt{b^2-4ac} \over 2a}.$$
        </body>
    </html>



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在浏览器中打开mathjax.html，会显示如下图：

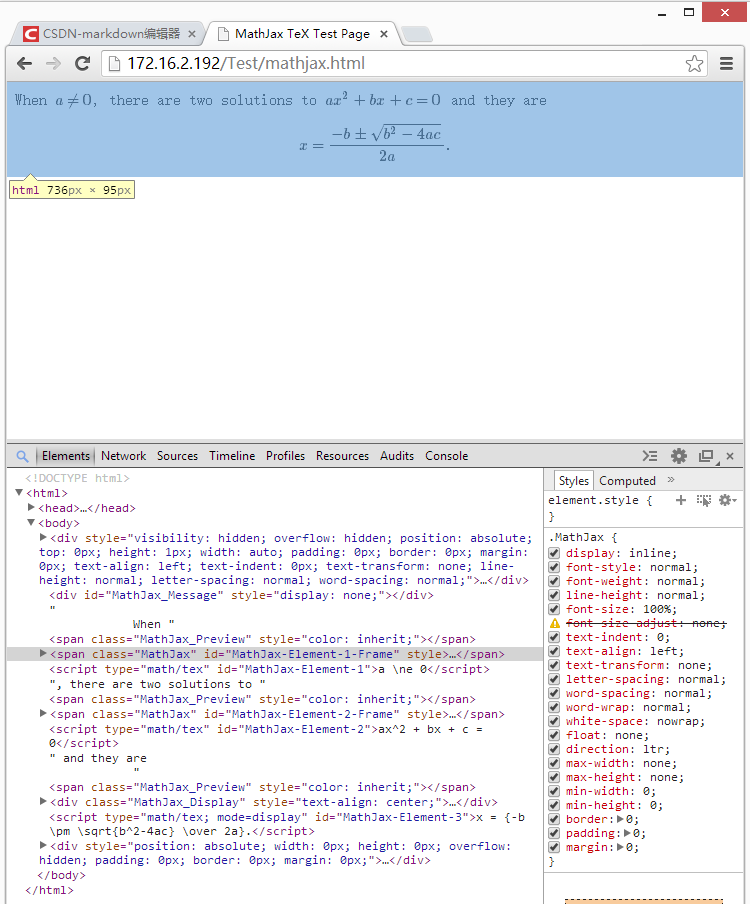
其对应的html代码如下图：

2.2 模拟MathJax渲染原理

从前面的例子可以看出，MathJax中数学公式是用一些特殊字符串表示的，这些字符串被特定的边界$ $和$$ $$包围。然后MathJax引擎会根据边界提取公式表达式，然后把它们替换成用户显示公式的html+css代码。

下面我们来模拟这一过程。用math.js模拟MathJax.js，如下所示：

window.onload = function()
{
    var body = document.getElementsByTagName('body')[0];
    var oldBody = body.innerHTML;
    var newBody = oldBody.replace(/[^$]\$([^$]+)\$[^$]/g, function(str, r1){
            return MathJax_inline(r1);
            });
    newBody = newBody.replace(/\$\$([^$]+)\$\$/g, function(str, r1){
            return MathJax_block(r1);
            });
    body.innerHTML  = newBody;
}

// 把公式内容描述转换为显示描述

function MathJax_inline(r1)

{

return '<span style="color:red">' + r1 + '</span>';

}

function MathJax_block(r1)

{

return '<div style="color:red">' + r1 + '</div>';

}



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

html页面相应修改：

<!DOCTYPE html>
<html>
    <head>
        <title>MathJax TeX Test Page</title>
        <script type="text/javascript" src="math.js"></script>
    </head>
    <body>
        When $a \ne 0$, there are two solutions to $ax^2 + bx + c = 0$ and they are
        $$x = {-b \pm \sqrt{b^2-4ac} \over 2a}.$$
    </body>
</html>



1
2
3
4
5
6
7
8
9
10
11

来看看效果：

虽然没有正确显示出公式，但是已经识别出了公式边界，并把公式部分用红色显示出来。真正的MathJax是把公式表达式替换成显示公式的html代码，而不是简单的设置为红色，但是这其中的处理原理是一致的。

3 CSDN-MarkDown编辑器常用数学公式输入教程

MathJax支持多种公式输入输出规范，输入格式可以是MathML, TeX，ASCIImath中的任何一种，输出格式可以是html+css，或svg，或MathML。下面仅对最常用的Tex输入规范进行说明。

3.1 公式定界符与关键字

CSDN-MarkDown编辑器使用的公式定界符为$和$$，单美元符号包围的是行内公式，双美元符号包围的是块公式。
Tex关键字（字符转义序列）表示特殊显示符号，如\frac表示分数，其后面可以跟随参数，参数多少与关键字有关。

3.2 上下标

^表示上标，_表示下标，如果上（下）标内容多于一个字符就需要使用{}，注意不是( ), 因为( )经常是公式本身组成部分，为避免冲突，所以选用了{ } 将其包起来。

示例：$x^{y^z}=(1+e^x)^{-2xy^w}$

效果：xyz=(1+ex)−2xywxyz=(1+ex)−2xyw

上面输入的上下标都是在字符的右侧，要想在左侧或者两侧都写上下标，那么需要使用\sideset语法。

示例：$\sideset{^1_2}{^3_4}\bigotimes$

效果：⨂12⨂34⨂21⨂43

3.3 括号和分隔符

( )和[ ]就是自身了，由于{ } 是Tex的元字符，所以表示它自身时需要转义。

示例：$f(x,y) = x^2 + y^2, x\epsilon[0,100]$

效果：f(x,y)=x2+y2,xϵ[0,100]，y={3,4,5}f(x,y)=x2+y2,xϵ[0,100]，y={3,4,5}

有时候括号需要大号的，普通括号不好看，此时需要使用\left和\right加大括号的大小。

示例：$(\frac{x}{y})^8$，$\left(\frac{x}{y}\right)^8$

效果：(xy)8(xy)8，(xy)8(xy)8

\left和\right必须成对出现，对于不显示的一边可以使用 . 代替。

示例：$\left.\frac{{\rm d}u}{{\rm d}x} \right| _{x=0}$

效果：dudx∣∣x=0dudx|x=0

3.4 分数

使用\frac{分子}{分母}格式，或者 分子\over 分母。

示例：$\frac{1}{2x+1}$或者$1\over{2x+1}$

效果：12x+112x+1 或者 12x+112x+1

3.5 开方

示例：$\sqrt[9]{3}$ 和 $\sqrt{3}$

效果：3–√939 和 3–√3

3.6 省略号

有两种省略号，\ldots 表示语文本底线对其的省略号，\cdots表示与文本中线对其的省略号。

示例：$f(x_1, x_2, \ldots, x_n)=x_1^2 + x_2^2+ \cdots + x_n^2$

效果：f(x1,x2,…,xn)=x21+x22+⋯+x2nf(x1,x2,…,xn)=x12+x22+⋯+xn2

3.7 矢量

示例：$\vec{a} \cdot \vec{b}=0$

效果: a⃗ ⋅b⃗ =0a→⋅b→=0

3.8 积分

示例：$\int_0^1x^2{\rm d}x $

效果： ∫10x2dx∫01x2dx

3.9 极限

示例：$\lim_{n\rightarrow+\infty}\frac{1}{n(n+1)}$

效果： limn→+∞1n(n+1)limn→+∞1n(n+1)

3.10 累加、累乘

示例：$\sum_1^n\frac{1}{x^2}$， $\prod_{i=0}^n\frac{1}{x^2}$

效果：∑n11x2∑1n1x2， ∏ni=01x2∏i=0n1x2

3.11 希腊字母

希腊字符示例：$$\alpha　A　\beta　B　\gamma　\Gamma　\delta　\Delta　\epsilon　E \varepsilon　　\zeta　Z　\eta　H　\theta　\Theta　\vartheta \iota　I　\kappa　K　\lambda　\Lambda　\mu　M　\nu　N \xi　\Xi　o　O　\pi　\Pi　\varpi　　\rho　P \varrho　　\sigma　\Sigma　\varsigma　　\tau　T　\upsilon　\Upsilon \phi　\Phi　\varphi　　\chi　X　\psi　\Psi　\omega　\Omega$$

效果：

α　A　β　B　γ　Γ　δ　Δ　ϵ　Eε　　ζ　Z　η　H　θ　Θ　ϑι　I　κ　K　λ　Λ　μ　M　ν　Nξ　Ξ　o　O　π　Π　ϖ　　ρ　Pϱ　　σ　Σ　ς　　τ　T　υ　Υϕ　Φ　φ　　χ　X　ψ　Ψ　ω　Ωα　A　β　B　γ　Γ　δ　Δ　ϵ　Eε　　ζ　Z　η　H　θ　Θ　ϑι　I　κ　K　λ　Λ　μ　M　ν　Nξ　Ξ　o　O　π　Π　ϖ　　ρ　Pϱ　　σ　Σ　ς　　τ　T　υ　Υϕ　Φ　φ　　χ　X　ψ　Ψ　ω　Ω

3.12 数学符号大汇总

±± ：\pm
×× ：\times
÷÷：\div
∣∣：\mid

⋅⋅：\cdot
∘∘：\circ
∗∗: \ast
⨀⨀：\bigodot
⨂⨂：\bigotimes
⨁⨁：\bigoplus
≤≤：\leq
≥≥：\geq
≠≠：\neq
≈≈：\approx
≡≡：\equiv
∑∑：\sum
∏∏：\prod
∐∐：\coprod

集合运算符：
∅∅：\emptyset
∈∈：\in
∉∉：\notin
⊂⊂：\subset
⊃⊃ ：\supset
⊆⊆ ：\subseteq
⊇⊇ ：\supseteq
⋂⋂ ：\bigcap
⋃⋃ ：\bigcup
⋁⋁ ：\bigvee
⋀⋀ ：\bigwedge
⨄⨄ ：\biguplus
⨆⨆：\bigsqcup

对数运算符：
loglog ：\log
lglg ：\lg
lnln ：\ln

三角运算符：
⊥⊥：\bot
∠∠：\angle
30∘30∘：30^\circ
sinsin ：\sin
coscos ：\cos
tantan ：\tan
cotcot ：\cot
secsec ：\sec
csccsc ：\csc

微积分运算符：
y′xy′x：\prime
∫∫：\int
∬∬ ：\iint
∭∭ ：\iiint
∬∬⨌：\iiiint
∮∮ ：\oint
limlim ：\lim
∞∞ ：\infty
∇∇：\nabla

逻辑运算符：
∵∵：\because
∴∴ ：\therefore
∀∀ ：\forall
∃∃ ：\exists
≠≠ ：\not=
≯≯：\not>
⊄⊄：\not\subset

戴帽符号：
y^y^ ：\hat{y}
yˇyˇ ：\check{y}
y˘y˘ ：\breve{y}

连线符号：
a+b+c+d¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯a+b+c+d¯：\overline{a+b+c+d}
a+b+c+d–––––––––––––a+b+c+d_ ：\underline{a+b+c+d}
a+b+c1.0+d2.0a+b+c⏟1.0+d⏞2.0：\overbrace{a+\underbrace{b+c}_{1.0}+d}^{2.0}

箭头符号：
↑↑：\uparrow
↓↓：\downarrow
⇑⇑ ：\Uparrow
⇓⇓：\Downarrow
→→：\rightarrow
←← ：\leftarrow
⇒⇒ ：\Rightarrow
⇐⇐ ：\Leftarrow
⟶⟶ ：\longrightarrow
⟵⟵ ：\longleftarrow
⟹⟹：\Longrightarrow
⟸⟸ ：\Longleftarrow

3.13 需要转义的字符

要输出字符　空格　#　$　%　&　_　{　}　，用命令：　\空格　#　\$　\%　\&　_　{　}

3.14 使用指定字体

{\rm text}如：
使用罗马字体：texttext ${\rm text}$
其他的字体还有：
\rm　　罗马体　　　　　　　\it　　意大利体
\bf　　黑体　　　　　　　　\cal 　花体
\sl　　倾斜体　　　　　　　\sf　　等线体
\mit 　数学斜体　　　　　　\tt　　打字机字体
\sc　　小体大写字母