Dijkstra算法 python实现

1.Dijkstra算法的基本实现 \(O(n^2)\)

简介：

Dijkstra算法是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

算法介绍推荐文章：

https://www.zhihu.com/question/20630094/answer/758191548

假设有图G：

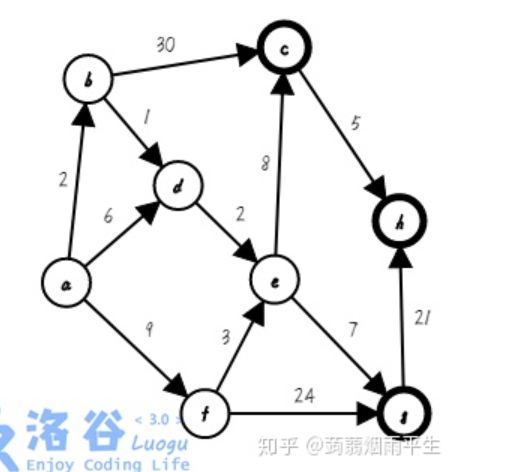
则G的带权邻接矩阵为：

matrix = [
    [99, 2, 99, 6, 99, 9, 99, 99],
    [99, 99, 30, 1, 99, 99, 99, 99],
    [99, 99, 99, 99, 99, 99, 99, 5],
    [99, 99, 99, 99, 2, 99, 99, 99],
    [99, 99, 8, 99, 99, 99, 7, 99],
    [99, 99, 99, 99, 3, 99, 24, 99],
    [99, 99, 99, 99, 99, 99, 99, 21],
    [99, 99, 99, 99, 99, 99, 99, 99]]

则时间复杂度为\(O\left( n^2 \right)\)的算法如下图（python语言）：

n = len(matrix) # 计算顶点数量

# v记录是否访问
# dis为起始结点到相邻结点的距离
v = [0]*n
dis = matrix[0].copy()

# 起始情况
v[0] = 1
dis[0] = 99

# 循环n次
for _ in range(n):
    # 找出与集合相邻且距离起点最近的点
    k = 0
    for j in range(n):
        if v[j] == 0 and dis[j] < dis[k]:
            k = j
	# 该点被访问
    v[k] = 1

    # 用该点进行松弛(relax)
    for j in range(n):
        if v[j] == 0 and dis[k] + matrix[k][j] < dis[j]:
            dis[j] = dis[k] + matrix[k][j]

结果：

dis = [99, 2, 13, 3, 5, 9, 12, 18]

2.从别的地方抄的虚假的和算法导论格式一样的堆优化实现

class Graph:
    def __init__(self):
        self.V = []
        self.w = {}

class Vertex:
    def __init__(self, x):
        self.key = x
        self.color = 'white'
        self.d = 10000
        self.pi = None
        self.adj = []

class Solution():
    def InitializeSingleSource(self, G, s):
        for v in G.V:
            v.d = 10000
            v.pi = None
        s.d = 0

    def Relax(self, u, v, w):
        if v.d > u.d + w[(u, v)]:
            v.d = u.d + w[(u, v)]
            v.pi = u

    def Dijkstra(self, G, w, s):
        self.InitializeSingleSource(G, s)
        S = set()
        Q = G.V[:]
        while Q:
            u = self.ExtractMin(Q, S)
            S.add(u)
            for v in u.adj:
                self.Relax(u, v, w)

    def ExtractMin(self, Q, S):
        Q.sort(key=lambda v: v.d)
        return Q.pop(0)

if __name__ == '__main__':
    s = Vertex('s')
    t = Vertex('t')
    y = Vertex('y')
    x = Vertex('x')
    z = Vertex('z')

    s.adj = [t, y]
    y.adj = [t, z, x]
    t.adj = [x, y]
    x.adj = [z]
    z.adj = [x, s]

    G = Graph()
    G.V = [s, t, y, x, z]
    G.w = {
        (s,t):10,
        (s,y):5,
        (t,y):2,
        (y,t):3,
        (t,x):1,
        (y,z):2,
        (x,z):4,
        (z,x):6,
        (y,x):9,
        (z,s):7
    }

    m = Solution()
    m.Dijkstra(G, G.w, s)

    for v in G.V:
        if v != s:
            print v.key, v.d, v.pi.key
        else:
            print v.key, v.d, v.pi