JPEG解码——(4)霍夫曼解码

本篇是该系列的第四篇，主要介绍霍夫曼解码相关内容。

承接上篇，文件头解析完毕后，就进入了编码数据区域，即SOS的tag后的区域，也是图片数据量的大头所在。

1. 解码过程规则描述

a）从此颜色分量单元数据流的起点开始一位一位的读入，直到读入的编码与该分量直流哈夫曼树的某个码字（叶子结点）一致，然后用直流哈夫曼树

查得该码字对应的权值。权值（共8位）表示该直流分量数值的二进制位数，也就是接下来需要读入的位数。

b）继续读入位数据，直到读入的编码与该分量交流哈夫曼树的某个码字（叶子结点）一致，然后用交流哈夫曼树查得该码字对应的权值。权值的高4位

表示当前数值前面有多少个连续的零，低4 位表示该交流分量数值的二进制位数，也就是接下来需要读入的位数。

c）不断重复步骤b，直到满足交流分量数据结束的条件。

而结束条件有两个，只要满足其中一个即可：

①当读入码字的权值为零，表示往后的交流变量全部为零；
②已经读入63个交流分量。

2. 待处理的数据区域

　　上面的规则描述过于抽象，需要一个例子来实战说明，仍使用那张animal_park.jpg的图片。

　　其二进制数据显示如下（FFDA所代表的SOS之后深色标注区域）：

　　截取到的二进制数据为：F9 96 8B FA 71 EA 5B 24 B5 ...

3. 准备好霍夫曼表

　　先列出四张霍夫曼表——DC0,AC0, DC1,AC1，待后面查找使用。

　　DC0——Y分量的直流部分

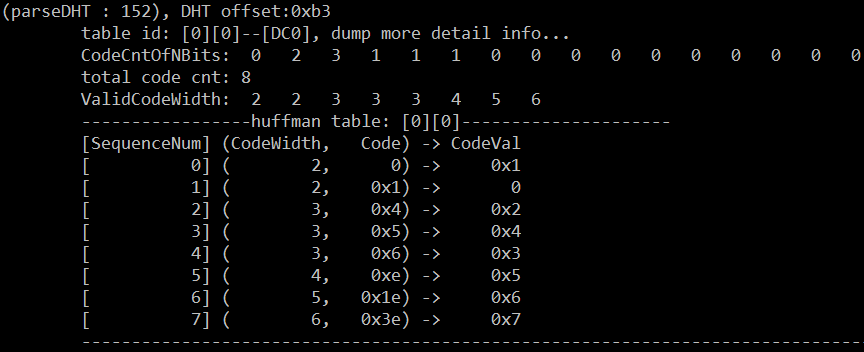
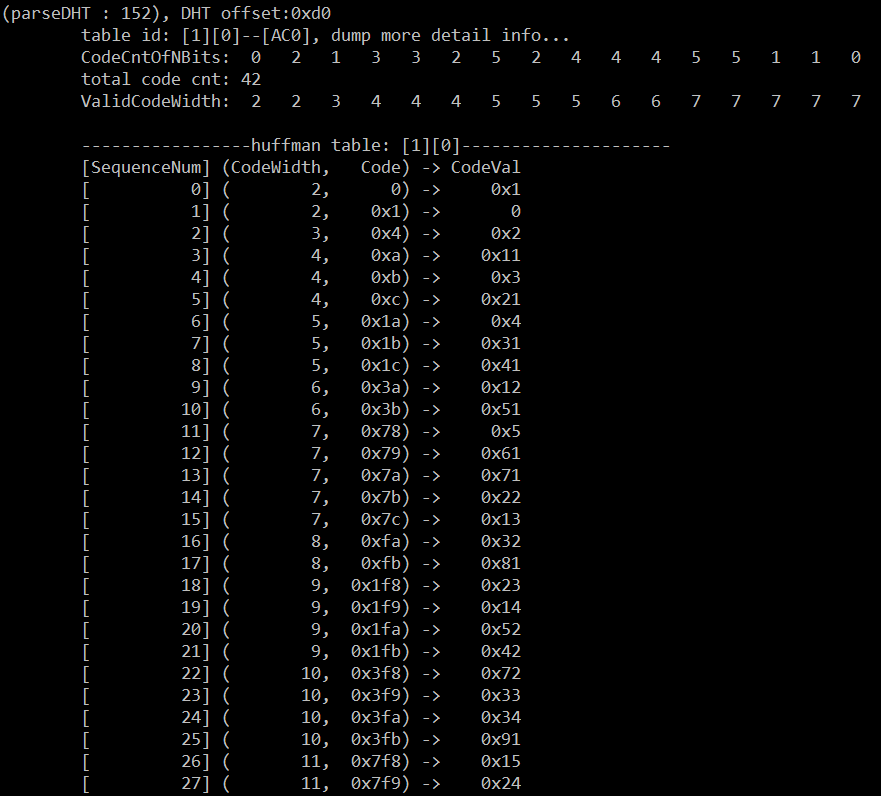
　　AC0——Y分量的交流部分（表太长，没列全）

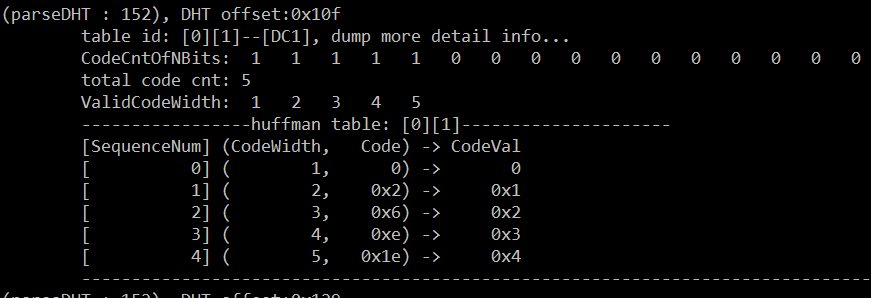
　　DC1——UV分量的直流部分

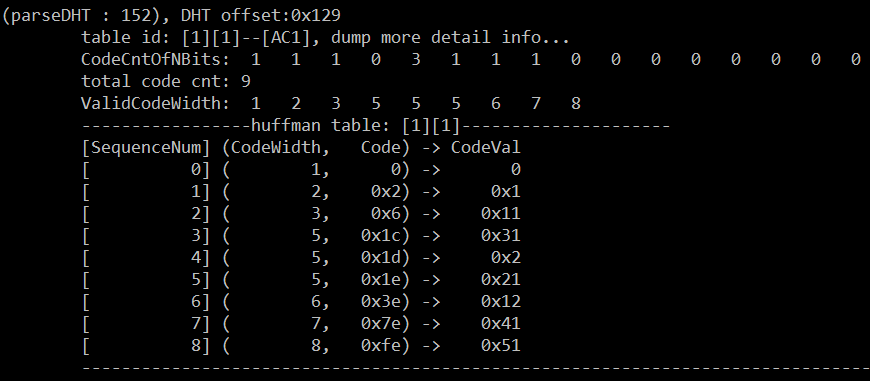
　　AC1——UV分量的交流部分

4. 解码步骤

　　这是难点所在，解码的过程其实就是霍夫曼树的查找过程。mcu单元内部使用了RLE行程编码和霍夫曼编码来压缩数据。

　　例子：F9 96 8B FA 71 EA 5B 24 B5。。。

　　对应的二进制位展开：1111 1001, 1001 0110, 1000 1011, 1111 1010, 0111 0001, 1110 1010, 0101 1011, 0010 0100, 1011 0101。。。

step1. 先读入若干位与DC0表的Code进行匹配。

读取2位的11时，  无匹配的Code，因为2位宽的Code只有0b00和0b01

3位的111        无                              3                           0b100，0b101和0b110。

4位的1111      无                              4                            0b1110。

5位的11111    无                              5                            0b11110。

6位的111110  有                              6                            0b111110，恰好匹配！其对应的CodeVal为0x7

step2. 利用上面得到的CodeVal进行拆分，并读取后面若干位。
　　0x7=0x07，高四位为0，低四位为7，则再读取后面的7位二进制，为：01, 1001 0。
　　后面读取的值，这样算：如果开头为1则为正数，如果开头为0，则为负数，然后对各位求反得到数值，即可。

　　01, 1001 0这个值，由于开头为0，则为负数，多少呢？取反得到：10, 01101 = 0x4D = 77，最后得到最终值为：-77。

step3. 通过上面两步骤的第一次扫描，得到的为Y分量的DC值，后面还需经过63次扫描得到剩余的AC值（一般扫描几次就结束了）。

　　上面DC值标记为-77。

step4. 继续通过类似step1和step2来取得AC值，注意要查找AC0表。

　　读取5位的110, 10时，有匹配的Code：0b11010=0x1a，其对应的CodeVal=0x04；
　　取得后四位的值——4，表示还需读取的二进制位数量，来表示真正的信源值——0b0010，经（step2中描述）变换后值为-13；
　　那么可以RLE标记为（0，-13），其中0来自于CodeVal的高4位，-13为另读入的数据值。可也记为key-val对。

step5. 重复step4的操作，直到得到(0，0)(位置为5B那个字节的最高四位)。

　　后面的依次为：

Code                                CodeVal          RLE_val        RLE

11, 1111 1010(0x3FA)         0x34            0111(-8)         (3, -8)

00                                        0x1              0 (-1)              (0, -1)

1, 1110 10(0x7A)                 0x71            1(1)                (7, 1)

00                                          0x1             1(1)                (0, 1)

01                                          0x0              --                   (0, 0)  -> 结束于5B的高4位

step6. 通过step1-step5的扫描，得到数据：-77, (0, -13), (3, -8),(0, -1),(7, 1), (0, 1), (0, 0)

step7. step1到step6结束后，表示一个mcu的霍夫曼解码结束。

　　RLE中的(m,n)，m表示前面填充0的个数，n表示实际值。

　　其解码结果如下：