MT【101】分配问题举例若干

先拿MT【100】的图表镇楼。

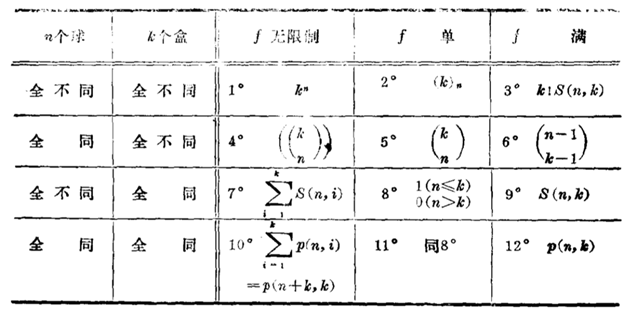
举几个例子：

【1】52张纸牌分发给4人，每人13张，问每人手中有一张小2的概率?

分析：第一步每人分一张小2，有4!种，然后48张牌平均分成4组有$\frac{48!}{12!12!12!12!}$易得概率为$4!\frac{48!(13!)^4}{52!(12!)^4}$大概为10.55%，有兴趣也可以算一下四张2都在某个人手里的概率。

【2】$(x+y+z+w)^5$的展开式有多少项？

分析：每一项都是5次方，相当于5个无区别的小球放入4个有标志的盒子里.每个盒子里放的球不加限制。也就是上表中第4种情况，有56种。$(x+y+z+w)^5$展开式如下：

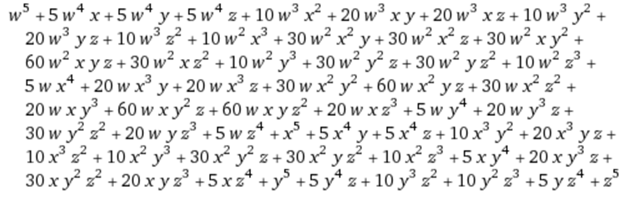
注：顺便讲一下$x^2y^2z^1w^0$前的系数计算公式为$\frac{5!}{2!2!1!0!}$可以类比二项式定理$(x+y)^5$展开中$x^2y^3$前的系数公式$\frac{5!}{2!3!}$。

【3】$x_1+x_2+\cdots+x_k\le n$的非负整数解的个数.

分析：定义如下映射$(x_1,x_2,\cdots,x_k)\mapsto (x_1+1,x_1+x_2+1,\cdots,x_1+\cdots+x_k+k)$是$x_1+x_2+\cdots+x_k\le n$的非负整数解集到$\{1,2,\cdots,n+k\}$中取$k$项严格单调递增数列集合的一个一一映射,有$\dbinom{k+n}{k}$

注：这里可以得到一个恒等式:$\sum_{i=0}^{n}\dbinom{k+i-1}{i}=\dbinom{k+n}{n}$

【4】已知$b_1+2b_2+\cdots+nb_n=n$其中$b_1,b_2,\cdots,b_n\in N$，把$\{1,2,\cdots,n\}$的一个全排列放入以下框架中

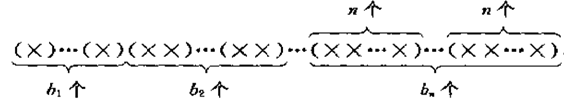
问有多少种不同形式.

答：$\frac{n!}{b_1!b_2!\cdots b_n!1^{b_1}2^{b_2}\cdots n^{b_n}}$即对称群$S_n$中$1^{b_1}2^{b_2}\cdots n^{b_n}$型的元素个数。