历届试题 小数第n位-（同余公式+快速幂）

问题描述

　　我们知道，整数做除法时，有时得到有限小数，有时得到无限循环小数。
　　如果我们把有限小数的末尾加上无限多个0，它们就有了统一的形式。

　　本题的任务是：在上面的约定下，求整数除法小数点后的第n位开始的3位数。

输入格式

　　一行三个整数：a b n，用空格分开。a是被除数，b是除数，n是所求的小数后位置（0<a,b,n<1000000000）

输出格式

　　一行3位数字，表示：a除以b，小数后第n位开始的3位数字。

样例输入

1 8 1

样例输出

125

样例输入

1 8 3

样例输出

500

样例输入

282866 999000 6

样例输出

914

 

百度找思路，基本都是循环，思路感觉太麻烦就没心思看下去，侥幸让我看到了数论解决方法，就借鉴一下，顺便截他的图。

佩服这些大牛能有这么方便的同余公式。b不一定和p互质，所以逆元不可行。

本题运用：

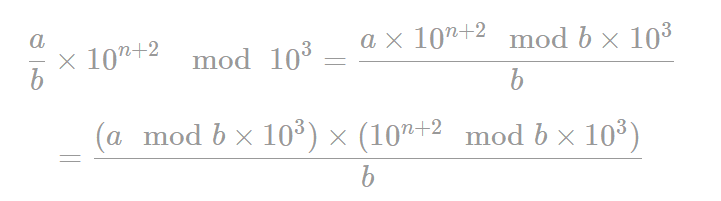
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<vector>
#include<stack>
#include<set>
#include<queue>
#include<cstring>
#define ll long long
using namespace std;

ll power(ll a,ll b,ll q)
{
    ll res=;
    while(b)
    {
        if(b%)
            res=res*a%q;
        b=b/;
        a=a*a%q;
    }
    return res%q;
}

int main()
{
    ll a,b,n,ans;
    while(cin>>a>>b>>n)
    {
        ll q=b*;
        ans = (a%q)*power(,n+,q);
        ans = ans/b;
        cout<<ans%<<endl;
    }
    return ;
}