Codeforces 1086 简要题解

文章目录

• A题
• B题
• C题
• D题
• E题

传送门

这场比赛原地爆炸了啊！！！

只做了两道。

A题

传送门 手贱没关freopenfreopenfreopen于是wawawa了一次，死活调不出错。

题意：给出网格图上三个点坐标，让你求出让三个点连通的最少网格数并且输出任意一种连接的方案。

---

思路：可以直接上分类讨论。

不过可以人脑减去一些讨论。

我们设最初的坐标为(x1,y1)，(x2,y2)，(x3,y3)(x_1,y_1)，(x_2,y_2)，(x_3,y_3)(x1​,y1​)，(x2​,y2​)，(x3​,y3​)

然后把x,yx,yx,y分别排序变成x1′,x2′,x3′x_1',x_2',x_3'x1′​,x2′​,x3′​和y1′,y2′,y3′y_1',y_2',y_3'y1′​,y2′​,y3′​

显然横向走的长度是x3−x1+1x_3-x_1+1x3​−x1​+1，我们不妨直接把(x1′,y2′)−>(x3′,y2′)(x_1',y_2')->(x_3',y_2')(x1′​,y2′​)−>(x3′​,y2′​)全部染上。

然后就只用考虑纵向的了。

于是我们找到yyy最小的点p(px,py)p(p_x,p_y)p(px​,py​)，把(px,py)−>(px,y1−1)(p_x,p_y)->(p_x,y_1-1)(px​,py​)−>(px​,y1​−1)染上，然后类似地去找到yyy最大的点q(qx,qy)q(q_x,q_y)q(qx​,qy​)，把(qx,qy)−>(qx,y1−1)(q_x,q_y)->(q_x,y_1-1)(qx​,qy​)−>(qx​,y1​−1)染上就可以满足题意了。

代码：

#include<bits/stdc++.h>
#define ri register int
using namespace std;
inline int read(){
	int ans=0;
	char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
	return ans;
}
int x[3],y[3],X[3],Y[3];
struct Pot{int x,y;}p[3];
inline bool cmp(const Pot&a,const Pot&b){return a.y==b.y?a.x<b.x:a.y<b.y;}
int main(){
	for(ri i=0;i<3;++i)p[i].x=x[i]=read(),p[i].y=y[i]=read();
	sort(x,x+3),sort(y,y+3),sort(p,p+3,cmp);
	int cnt=0;
	vector<pair<int,int> >ans;
	for(ri i=x[0];i<=x[2];++i)ans.push_back(make_pair(i,y[1]));
	for(ri i=y[0];i<y[1];++i)ans.push_back(make_pair(p[0].x,i));
	for(ri i=y[1]+1;i<=y[2];++i)ans.push_back(make_pair(p[2].x,i));
	cout<<ans.size()<<'\n';
	for(ri i=0;i<ans.size();++i)cout<<ans[i].first<<' '<<ans[i].second<<'\n';
	return 0;
}

B题

传送门 简单贪心

---

题意：给出一棵带权树的边长总和SSS和树的边，让你任意给每条边分配非负边权使得树的直径最小。

---

思路：我们考虑只赋值给连向叶子的边权值，且每条边的权值都是s叶子数\frac s{叶子数}叶子数s​，而其它边都赋值为0.

此时的答案为2s叶子数\frac{2s}{叶子数}叶子数2s​，不难证明改变任意一条当前边的权值都无法使答案更优，因此答案就是2s叶子数\frac{2s}{叶子数}叶子数2s​

代码：

#include<bits/stdc++.h>
#define ri register int
using namespace std;
inline int read(){
	int ans=0;
	char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
	return ans;
}
const int N=1e5+5;
int n,s,cnt=0,du[N];
int main(){
	n=read(),s=read()<<1;
	for(ri i=1;i<n;++i)++du[read()],++du[read()];
	for(ri i=1;i<=n;++i)if(du[i]==1)++cnt;
	printf("%.10lf",(double)s/cnt);
	return 0;
}

C题

传送门 贪心好题

题意：给出三个字符串S,A,BS,A,BS,A,B和字符集大小kkk，问是否存在一种字符集的双射关系使得SSS映射成的新字符串S′S'S′满足A≤S′≤BA\le S'\le BA≤S′≤B，允许输出任意一种方案。

---

思路：我们根据AAA字符串逐位贪心确定SSS，考虑当前SSS的字符sis_isi​和AAA当前的字符aia_iai​

1. 这个字符之前映射过了，那么直接判断：如果映射值si′&lt;ais_i'&lt;a_isi′​<ai​显然不满足条件；如果si′=ais_i'=a_isi′​=ai​就递归到下一位处理；如果si′&gt;ais_i'&gt;a_isi′​>ai​就直接贪心构造之后的位跟BBB比大小即可。
2. 这个字符之前没有映射过，那么先看能否映射成aia_iai​，如果可以就递归到下一位;否则看能否映射成一个比aia_iai​大的，如果可以就贪心构造之后的位跟BBB比较大小。

代码：

#include<bits/stdc++.h>
#define ri register int
using namespace std;
inline int read(){
	int ans=0;
	char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
	return ans;
}
const int N=1e6+5;
int n,Tran[26],tran[26],a[N],b[N],s[N],ans[N],vis[26],Vis[26],k;
char S[N];
inline void print(){
	puts("YES");
	for(ri i=0;i<=k;++i)if(Tran[i]==-1)for(ri j=0;j<=k;++j)if(!Vis[j]){Vis[Tran[i]=j]=1;break;}
	for(ri i=0;i<=k;++i)printf("%c",(char)(Tran[i]+'a'));
	puts("");
}
inline bool update(int st){
	for(ri i=0;i<=k;++i)Vis[i]=vis[i],Tran[i]=tran[i];
	for(ri i=st;i<=n;++i){
		if(Tran[s[i]]==-1)for(ri j=0;j<=k;++j)if(!Vis[j]){Vis[Tran[s[i]]=j]=1;break;}
		ans[i]=Tran[s[i]];
	}
	for(ri i=1;i<=n;++i){
		if(ans[i]==b[i])continue;
		if(ans[i]<b[i])return print(),true;
		return false;
	}
	return print(),true;
}
inline bool dfs(int pos){
	if(pos==n+1)return update(pos);
	if(~tran[s[pos]]){
		ans[pos]=tran[s[pos]];
		if(tran[s[pos]]<a[pos])return false;
		if(tran[s[pos]]==a[pos])return dfs(pos+1);
		return update(pos+1);
	}
	bool t;
	if(!vis[a[pos]]){
		vis[ans[pos]=tran[s[pos]]=a[pos]]=1,t=dfs(pos+1);
		if(t)return true;
		tran[s[pos]]=-1,ans[pos]=vis[a[pos]]=0;
	}
	for(ri i=a[pos]+1;i<=k;++i)
		if(!vis[i]){
			vis[ans[pos]=tran[s[pos]]=i]=1,t=update(pos+1);
			if(t)return true;
			return tran[s[pos]]=-1,vis[i]=0;
		}
	return false;
}
int main(){
	for(ri tt=read();tt;--tt){
		k=read()-1;
		scanf("%s",S+1),n=strlen(S+1);
		for(ri i=1;i<=n;++i)s[i]=S[i]-'a';
		scanf("%s",S+1);
		for(ri i=1;i<=n;++i)a[i]=S[i]-'a';
		scanf("%s",S+1);
		for(ri i=1;i<=n;++i)b[i]=S[i]-'a';
		for(ri i=0;i<26;++i)tran[i]=-1,vis[i]=0;
		if(!dfs(1))puts("NO");
	}
	return 0;
}

D题

传送门 思维好题

题意：nnn个人排成一排来猜拳，每个人规定每次出的是石头，剪刀或者布（这个规定可以修改）。允许操作n−1n-1n−1次，每次操作可以选当前剩下的两个相邻的人进行比赛，输了的进行淘汰（如果出的相同你可以自己定输赢），每次修改后问有多少人可能赢得最后胜利。

---

思路 ：分情况讨论废话

1. 所有人都出一样的：答案为nnn
2. 只出了两种，答案为出较大的人数。
3. 三种都有出的，发现对于一个人有没有可能赢，只跟左边，右边能否可以消成都不比自己大的有关，因此我们用setsetset维护一下每种出法最靠左和最靠右的位置然后容斥一下即可。

代码：

#include<bits/stdc++.h>
#define ri register int
using namespace std;
inline int read(){
	int ans=0;
	char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
	return ans;
}
const int N=2e5+5;
int ans=0,n,q,a[N],bit[N][3];
char s[N];
map<char,int>S;
set<int>pos[3];
inline int lowbit(int x){return x&-x;}
inline void update(int x,int id,int v){for(ri i=x;i<=n;i+=lowbit(i))bit[i][id]+=v;}
inline int query(int x,int id){int ret=0;for(ri i=x;i;i-=lowbit(i))ret+=bit[i][id];return ret;}
set<int>::iterator it;
inline void calc(){
	ans=0;
	for(ri i=0;i<3;++i){
		int x=(i+1)%3,y=(i+2)%3,lx,ly,rx,ry;
		ans+=pos[i].size();
		if(!pos[i].size()||!pos[x].size())continue;
		if(!pos[y].size()){ans-=pos[i].size();continue;}
		lx=*pos[x].begin(),rx=*pos[x].rbegin(),ly=*pos[y].begin(),ry=*pos[y].rbegin();
		if(ly>lx)ans-=query(ly,i)-query(lx-1,i);
		if(ry<rx)ans-=query(rx,i)-query(ry-1,i);
	}
}
int main(){
	n=read(),q=read(),S['R']=0,S['P']=1,S['S']=2,scanf("%s",s+1);
	for(ri i=1;i<=n;++i)a[i]=S[s[i]],pos[a[i]].insert(i),update(i,a[i],1);
	calc(),cout<<ans<<'\n';
	while(q--){
		int p=read();
		char t[2];
		scanf("%s",t);
		pos[a[p]].erase(p),update(p,a[p],-1);
		a[p]=S[t[0]];
		pos[a[p]].insert(p),update(p,a[p],1);
		calc(),cout<<ans<<'\n';
	}
	return 0;
}

---

E题

传送门 计数好题

题意简述：定义一个n∗nn*nn∗n矩阵是好的当它满足如下条件：

1. 这个矩阵每一行都是111~nnn的排列
2. 对于这个矩阵任意相邻两行都不存在一个位置使得这两行的这个位置上的数相同。

现在给你一个好的矩阵问它在所有n∗nn*nn∗n的好的矩阵当中的字典序排名。

n≤2000n\le2000n≤2000

---

思路：

显然需要从上往下从左往右一个一个算，我们考虑令ansi,jans_{i,j}ansi,j​表示按照从上往下从左往右一个一个填充使得到第(i,j)(i,j)(i,j)个格子之前的所有格子都已经跟给出的矩阵相同，而(i,j)(i,j)(i,j)这个格子填的数强制跟原矩阵不同，使得构造出的新矩阵字典序小于原矩阵的方案数。

这个定义看起来比较复杂但理解起来比较简单，我们来看这个图（我画图用得不好请原谅）：



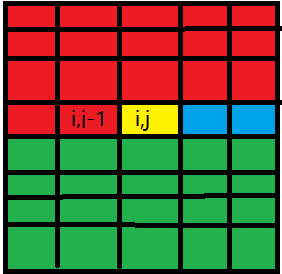
我们会发现，我们刚刚定义的状态说的就是红色部分跟原矩阵一样，第(i,j)(i,j)(i,j)号格子上面填的数要比原矩阵的数小的意思。

那么为啥(i,j)(i,j)(i,j)后面的格子分了两种颜色，绿色和蓝色呢？

假设我们已经知道了黄色和蓝色那一坨的总填法数，那么我们可以将第iii行看成一个数列，第i+1i+1i+1行的填法就是nnn个数排列的错排数，而对于第i+1i+1i+1行的每一种情况，第i+2i+2i+2行的填法又是nnn个数排列的错排数…于是后面n−in-in−i行的填法数就是n个数错排数n−in个数错排数^{n-i}n个数错排数n−i

于是我们只需要求出来黄蓝色部分的填法数啦！

考虑到黄色部分其实很好算填法数，我们只用维护一个以权值为下标的树状数组就可以动态统计黄色部分的选法数，关键在于蓝色部分，我们发现好像蓝色部分的选法数跟上面一行有关，仔细分析之后可以发现就是让你求nnn个数有mmm个数强制错排的方案数。

这个东西是可以用dpdpdp解决的。

设fi,jf_{i,j}fi,j​表示iii个数jjj个数强制错排的方案数。

于是就相当于iii个数j−1j-1j−1个数强制错排的方案数扣去不合法的方案数，什么时候不合法？有一个本该错排并没有错排，因此这时候剩下i−1i-1i−1个数有j−1j-1j−1个数强制错排，故推导出了fi,j=fi,j−1−fi−1,j−1f_{i,j}=f_{i,j-1}-f_{i-1,j-1}fi,j​=fi,j−1​−fi−1,j−1​

这个时候差不多已经做完了。

只需要对于第(i,j)(i,j)(i,j)号格子讨论它选出来填上去的值出现过几次就行了。

代码：

#include<bits/stdc++.h>
#define ri register int
using namespace std;
typedef long long ll;
inline int read(){
	int ans=0;
	char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
	return ans;
}
const int mod=998244353,N=2005;
inline int add(int a,int b){return a+b>=mod?a+b-mod:a+b;}
inline int dec(int a,int b){return a>=b?a-b:a-b+mod;}
inline int mul(int a,int b){return (ll)a*b%mod;}
int n,fac[N],mult[N],ans=0,a[N][N],f[N][N],vis[N];
struct Bit{
	int bit[N];
	Bit(){memset(bit,0,sizeof(bit));}
	inline int lowbit(int x){return x&-x;}
	inline void update(int x,int v){for(ri i=x;i<=n;i+=lowbit(i))bit[i]+=v;}
	inline int query(int x){int ret=0;for(ri i=x;i;i-=lowbit(i))ret+=bit[i];return ret;}
	inline void clear(){fill(bit+1,bit+n+1,0);}
}A,B;
int main(){
	fac[0]=fac[1]=1,n=read(),mult[0]=1,f[1][0]=1;
	for(ri i=2;i<=n;++i){
		fac[i]=f[i][0]=mul(fac[i-1],i);
		for(ri j=1;j<=i;++j)f[i][j]=dec(f[i][j-1],f[i-1][j-1]);
	}
	for(ri i=1;i<=n;++i)for(ri j=1;j<=n;++j)a[i][j]=read();
	for(ri i=1;i<=n;++i)mult[i]=mul(mult[i-1],f[n][n]);
	A.clear();
	for(ri i=1;i<=n;++i)ans=add(ans,mul(fac[n-i],a[1][i]-1-A.query(a[1][i]-1))),A.update(a[1][i],1);
	ans=mul(ans,mult[n-1]);
	for(ri i=2,sum;i<=n;++i){
		sum=0,A.clear(),B.clear(),fill(vis+1,vis+n+1,0);
		for(ri x,y,t,j=n;j;--j){
			if(++vis[a[i][j]]==2)B.update(a[i][j],1);
			if(++vis[a[i-1][j]]==2)B.update(a[i-1][j],1);
			A.update(a[i][j],1),x=B.query(a[i][j]-1),y=A.query(a[i][j]-1)-x,t=B.query(n);
			if(a[i-1][j]<a[i][j]&&vis[a[i-1][j]]==2)--x;
			if(vis[a[i-1][j]]==2)--t;
			sum=add(sum,mul(x,f[n-j][t-1])),sum=add(sum,mul(y,f[n-j][t]));
		}
		ans=add(ans,mul(sum,mult[n-i]));
	}
	cout<<ans;
	return 0;
}