python 回溯法 子集树模板 系列 —— 1、8 皇后问题

问题

8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

分析

为了简化问题，考虑到8个皇后不同行，则每一行放置一个皇后，每一行的皇后可以放置于第0、1、2、...、7列，我们认为每一行的皇后有8种状态。那么，我们只要套用子集树模板，从第0行开始，自上而下，对每一行的皇后，遍历它的8个状态即可。

代码

'''
8皇后问题
'''

n = 8
x = []  # 一个解（n元数组）
X = []  # 一组解

# 冲突检测：判断 x[k] 是否与前 x[0~k-1] 冲突
def conflict(k):
    global x

    for i in range(k):                              # 遍历前 x[0~k-1]
        if x[i]==x[k] or abs(x[i]-x[k])==abs(i-k):  # 判断是否与 x[k] 冲突
            return True
    return False

# 套用子集树模板
def queens(k): # 到达第k行
    global n, x, X

    if k >= n:         # 超出最底行
        #print(x)
        X.append(x[:]) # 保存（一个解），注意x[:]
    else:
        for i in range(n):  # 遍历第 0~n-1 列（即n个状态）
            x.append(i)     # 皇后置于第i列，入栈
            if not conflict(k): # 剪枝
                queens(k+1)
            x.pop()         # 回溯，出栈

# 解的可视化（根据一个解x，复原棋盘。'X'表示皇后）
def show(x):
    global n

    for i in range(n):
        print('. ' * (x[i]) + 'X ' + '. '*(n-x[i]-1))

# 测试
queens(0) # 从第0行开始

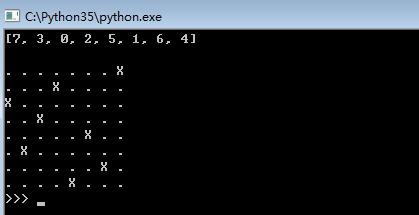
print(X[-1], '\n')
show(X[-1])

效果图