[机器学习笔记]奇异值分解SVD简介及其在推荐系统中的简单应用

本文先从几何意义上对奇异值分解SVD进行简单介绍，然后分析了特征值分解与奇异值分解的区别与联系，最后用python实现将SVD应用于推荐系统。

1.SVD详解

SVD(singular value decomposition)，翻译成中文就是奇异值分解。SVD的用处有很多，比如：LSA（隐性语义分析）、推荐系统、特征压缩（或称数据降维）。SVD可以理解为：将一个比较复杂的矩阵用更小更简单的3个子矩阵的相乘来表示，这3个小矩阵描述了大矩阵重要的特性。

1.1奇异值分解的几何意义(因公式输入比较麻烦所以采取截图的方式)

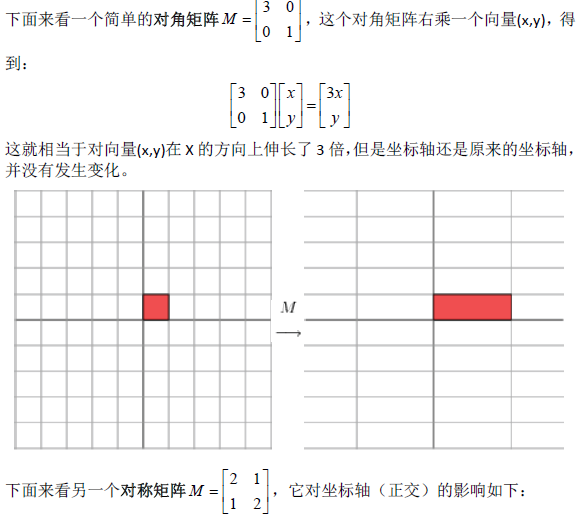
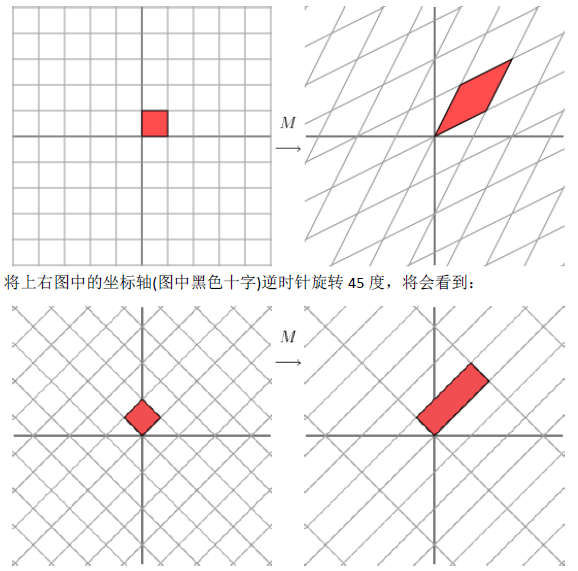
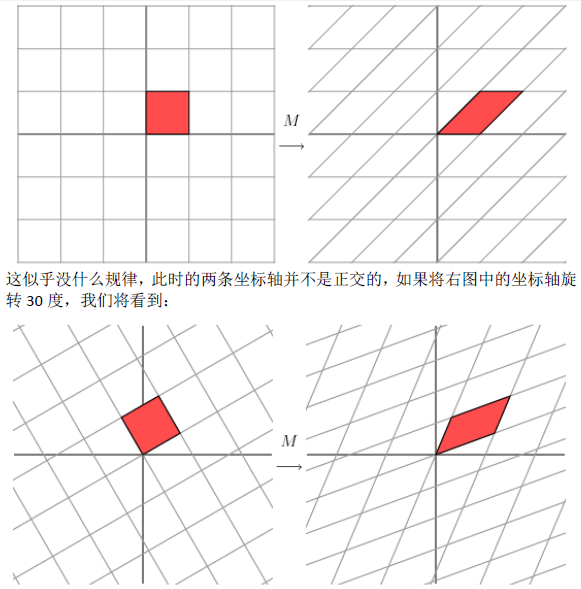
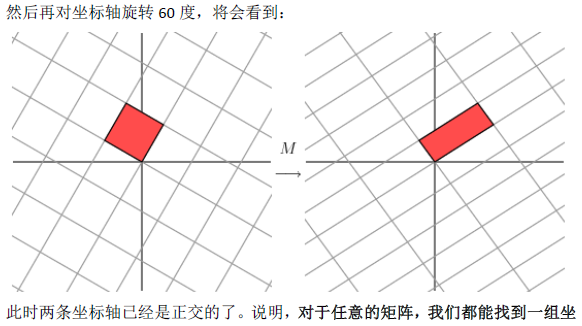
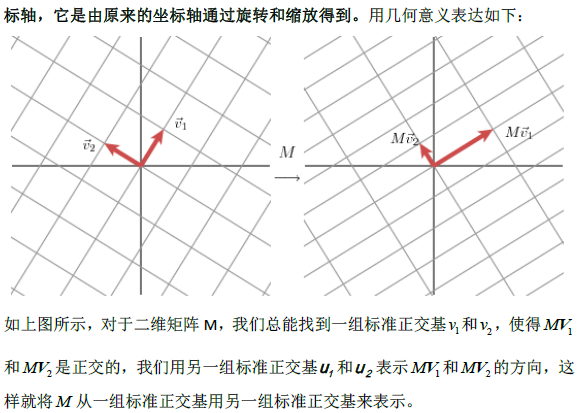
2.SVD应用于推荐系统

数据集中行代表用户user，列代表物品item，其中的值代表用户对物品的打分。基于SVD的优势在于：用户的评分数据是稀疏矩阵，可以用SVD将原始数据映射到低维空间中，然后计算物品item之间的相似度，可以节省计算资源。

整体思路：先找到用户没有评分的物品，然后再经过SVD“压缩”后的低维空间中，计算未评分物品与其他物品的相似性，得到一个预测打分，再对这些物品的评分从高到低进行排序，返回前N个物品推荐给用户。

具体代码如下，主要分为5部分：

第1部分：加载测试数据集；

第2部分：定义三种计算相似度的方法；

第3部分：通过计算奇异值平方和的百分比来确定将数据降到多少维才合适，返回需要降到的维度；

第4部分：在已经降维的数据中，基于SVD对用户未打分的物品进行评分预测，返回未打分物品的预测评分值；

第5部分：产生前N个评分值高的物品，返回物品编号以及预测评分值。

优势在于：用户的评分数据是稀疏矩阵，可以用SVD将数据映射到低维空间，然后计算低维空间中的item之间的相似度，对用户未评分的item进行评分预测，最后将预测评分高的item推荐给用户。

#coding=utf-8
from numpy import *
from numpy import linalg as la
 
'''加载测试数据集'''
def loadExData():
    return mat([[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
           [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
           [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
           [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
           [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
           [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
           [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
           [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
           [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
           [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
           [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]])
 
'''以下是三种计算相似度的算法，分别是欧式距离、皮尔逊相关系数和余弦相似度,
注意三种计算方式的参数inA和inB都是列向量'''
def ecludSim(inA,inB):
    return 1.0/(1.0+la.norm(inA-inB))  #范数的计算方法linalg.norm()，这里的1/(1+距离)表示将相似度的范围放在0与1之间
 
def pearsSim(inA,inB):
    if len(inA)<3: return 1.0
    return 0.5+0.5*corrcoef(inA,inB,rowvar=0)[0][1]  #皮尔逊相关系数的计算方法corrcoef()，参数rowvar=0表示对列求相似度，这里的0.5+0.5*corrcoef()是为了将范围归一化放到0和1之间
 
def cosSim(inA,inB):
    num=float(inA.T*inB)
    denom=la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom) #将相似度归一到0与1之间
 
'''按照前k个奇异值的平方和占总奇异值的平方和的百分比percentage来确定k的值,
后续计算SVD时需要将原始矩阵转换到k维空间'''
def sigmaPct(sigma,percentage):
    sigma2=sigma**2 #对sigma求平方
    sumsgm2=sum(sigma2) #求所有奇异值sigma的平方和
    sumsgm3=0 #sumsgm3是前k个奇异值的平方和
    k=0
    for i in sigma:
        sumsgm3+=i**2
        k+=1
        if sumsgm3>=sumsgm2*percentage:
            return k
 
'''函数svdEst()的参数包含：数据矩阵、用户编号、物品编号和奇异值占比的阈值，
数据矩阵的行对应用户，列对应物品，函数的作用是基于item的相似性对用户未评过分的物品进行预测评分'''
def svdEst(dataMat,user,simMeas,item,percentage):
    n=shape(dataMat)[1]
    simTotal=0.0;ratSimTotal=0.0
    u,sigma,vt=la.svd(dataMat)
    k=sigmaPct(sigma,percentage) #确定了k的值
    sigmaK=mat(eye(k)*sigma[:k])  #构建对角矩阵
    xformedItems=dataMat.T*u[:,:k]*sigmaK.I  #根据k的值将原始数据转换到k维空间(低维),xformedItems表示物品(item)在k维空间转换后的值
    for j in range(n):
        userRating=dataMat[user,j]
        if userRating==0 or j==item:continue
        similarity=simMeas(xformedItems[item,:].T,xformedItems[j,:].T) #计算物品item与物品j之间的相似度
        simTotal+=similarity #对所有相似度求和
        ratSimTotal+=similarity*userRating #用"物品item和物品j的相似度"乘以"用户对物品j的评分"，并求和
    if simTotal==0:return 0
    else:return ratSimTotal/simTotal #得到对物品item的预测评分
 
'''函数recommend()产生预测评分最高的N个推荐结果，默认返回5个；
参数包括：数据矩阵、用户编号、相似度衡量的方法、预测评分的方法、以及奇异值占比的阈值；
数据矩阵的行对应用户，列对应物品，函数的作用是基于item的相似性对用户未评过分的物品进行预测评分；
相似度衡量的方法默认用余弦相似度'''
def recommend(dataMat,user,N=5,simMeas=cosSim,estMethod=svdEst,percentage=0.9):
    unratedItems=nonzero(dataMat[user,:].A==0)[1]  #建立一个用户未评分item的列表
    if len(unratedItems)==0:return 'you rated everything' #如果都已经评过分，则退出
    itemScores=[]
    for item in unratedItems:  #对于每个未评分的item，都计算其预测评分
        estimatedScore=estMethod(dataMat,user,simMeas,item,percentage)
        itemScores.append((item,estimatedScore))
    itemScores=sorted(itemScores,key=lambda x:x[1],reverse=True)#按照item的得分进行从大到小排序
    return itemScores[:N]  #返回前N大评分值的item名，及其预测评分值

将文件命名为svd2.py,在python提示符下输入：

>>>import svd2
>>>testdata=svd2.loadExData()
>>>svd2.recommend(testdata,1,N=3,percentage=0.8)#对编号为1的用户推荐评分较高的3件商品

Reference:

1.Peter Harrington，《机器学习实战》，人民邮电出版社，2013

2.http://www.ams.org/samplings/feature-column/fcarc-svd (讲解SVD非常好的一篇文章，对于理解SVD非常有帮助，本文中SVD的几何意义就是参考这篇)

3. http://blog.csdn.net/xiahouzuoxin/article/details/41118351 （讲解SVD与特征值分解区别的一篇文章）