BZOJ 1912: [Apio2010]patrol 巡逻 （树的直径）(详解)

题目：

　　https://www.lydsy.com/JudgeOnline/problem.php?id=1912

题解：

　　首先，显然当不加边的时候，遍历一棵树每条边都要经过两次。那么现在考虑k==1的情况，考虑加入的这一条边有什么作用。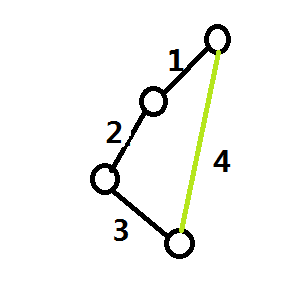

显然，如图4边的作用就是使得原来的1-2-3-3-2-1路线变为了4-3-2-1或1-2-3-4，那么作用就是以多走一步的代价使得这条新边两端的两个结点的遍历路径长度减半。

　　因此，想要使路径最短，就要使这条新边两端的两个结点之间的距离更长，显然，当两端的结点在原树中的路径为原树的直径时取得k==1时的最优解。设直径长度为dis，则k==1时ans=（n-1）*2-dis+1。

　　那么，k==2的时候怎么办呢。显然直接求次长链的做法是错的，因为求次长链的时候会与直径的某些边重复，那么这些边就是没有意义的，答案显然不更优。

　　因此，我们采用另一种方法：将直径上的边权全部置成-1，然后再跑一遍最长链。开始我也很不懂为什么要置成-1而不置成0，欸还是上面那张图是因为你考虑当你通过4边走到最下面那个点之后，显然你还是要回到最初的点的，而如果路径上的边与之前的直径重复，那么等于说你多加了一遍这条边，因此置成-1后不就相当于没加吗

　　P.S.当边权有负数时求直径不能用两边dfs，而应该用dp。WA了好久qwq。。。于是我第一遍求直径时用的两边dfs，第二遍用的dp。。。

代码：

#include<bits/stdc++.h>

using namespace std;

const int maxn=;
int dep[maxn],fa[maxn],head[maxn],cnt=,root,ans,n,k,mdep[maxn],maxx;

struct ed{
    int next,to,w;
}e[maxn<<];

void add(int u,int v){
    e[++cnt]=(ed){head[u],v,},head[u]=cnt;
    e[++cnt]=(ed){head[v],u,},head[v]=cnt;
}

void dfs(int now,int f){
    fa[now]=f;mdep[now]=;
    for(int i=head[now];i;i=e[i].next){
        int tt=e[i].to;
        if(tt==f) continue;
        dep[tt]=dep[now]+e[i].w;
        dfs(tt,now);    mdep[now]=max(mdep[now],mdep[tt]+e[i].w);
    }
}

void dp(int now,int f){
    int fm=-,sm=-;
    for(int i=head[now];i;i=e[i].next){
        int tt=e[i].to;
        if(tt==f) continue;
        if(mdep[tt]+e[i].w>sm){
            if(mdep[tt]+e[i].w>fm)
                swap(fm,sm),fm=mdep[tt]+e[i].w;
            else
                sm=mdep[tt]+e[i].w;
        }
        dp(tt,now);
    }
    maxx=max(maxx,fm+sm);
    maxx=max(maxx,fm);
    maxx=max(maxx,sm);
}

int main(){
    scanf("%d%d",&n,&k);
    int u,v;
    for(int i=;i<n;i++)
        scanf("%d%d",&u,&v),add(u,v);
    dfs(,);root=;
    for(int i=;i<=n;i++)
        if(dep[i]>dep[root])
            root=i;
    dep[root]=,dfs(root,);
    for(int i=;i<=n;i++)
        if(dep[i]>dep[root])
            root=i;
    ans=(n-)*-dep[root]+;
    if(k==){
        while(fa[root])
            for(int i=head[root];i;i=e[i].next){
                int tt=e[i].to;
                if(tt==fa[root]){
                    e[i].w=e[i^].w=-;
                    root=fa[root];break;
                }
            }
        dep[]=;maxx=-0x3f3f3f3f;
        dfs(,);dp(,);
        ans-=maxx-;
    }
    printf("%d",ans);
    return ;
}