一窍懂PID

这是学习PID时的理解，做个笔记！

一：首选，说一下一些基本概念，为了更好理解。

PID：就是对输入偏差进行比例积分微分运算，运算的叠加结果去控制执行机构。

　　P（proportion）：比例，就是对输入偏差乘以一个系数。

　　I（integration）：积分，就是对输入偏差进行积分运算。

　　D（differentiation）：微分，就是对输入偏差进行微分运算。

动态偏差：在调节过程中，被调量和设定值之间的偏差随时间改变，任意时刻两者之间的偏差叫做动态偏差，简称动差。

静态偏差：调节趋于稳定之后，被调量和设定值之间还存在的偏差叫做静态偏差，简称静差。

传递函数：是对线性微分方程在零初始条件下进行拉普拉斯变换得到的。

　　与微分方程的相通性：U(S):输入信号的拉普拉斯变换   Y(S)：输出信号的拉普拉斯变换

　　　　

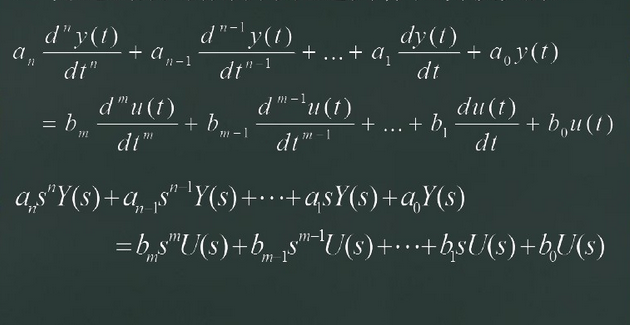
　　传递函数的两种形式：

　　　　

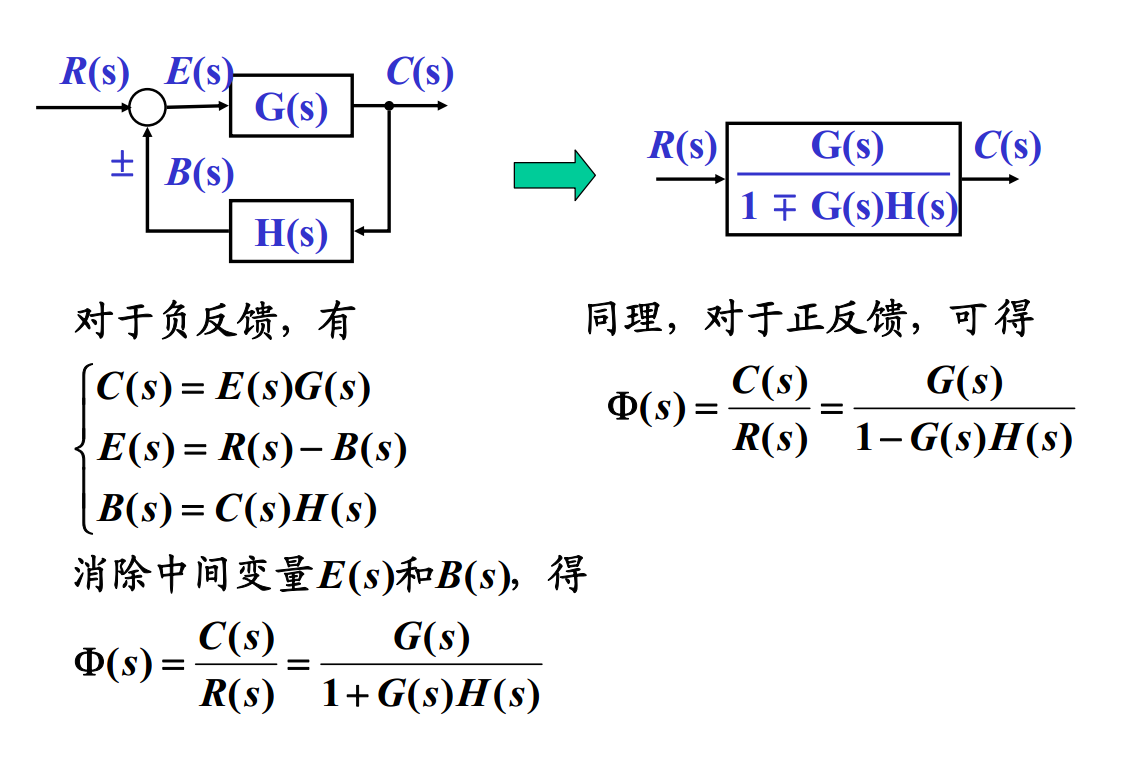
　　闭环传递函数公式：

　　　　

线性系统稳定性充要条件：

　　　　

系统动态性能说明：

　　

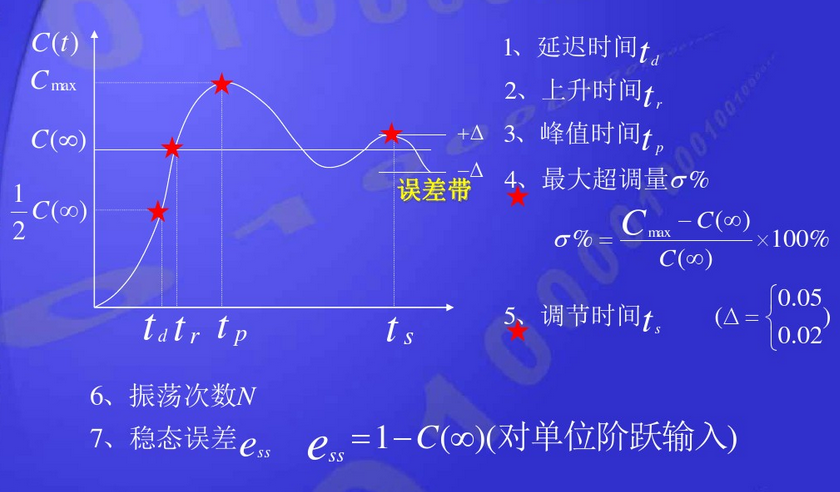
　　a,其中，对于没有震荡的系统，tr指响应从终值10%上升到终值90%所需要的时间。上升时间反应系统的响应速度，上升时间越短，说明系统响应速度越快。

　　b,调节时间ts反应系统过渡过程时间的长短。

　　c,tr,tp,ts表示控制系统响应的快速性，最大超调量，N反应系统动态过程的平稳性。

　　d,控制系统动态过程的平稳性和快速性指标之间往往存在相互制约的关系，例如要想响应速度更快（即tr更小），往往引起系统的超调量加大。相反，如果要保持小幅度的超调，通常也会延长系统的过度时间。

　　e,在保持系统不出现大的超调的前提下，尽量提升系统的响应速度，是控制系统设计的主要目标之一。

PID的结构：

　　

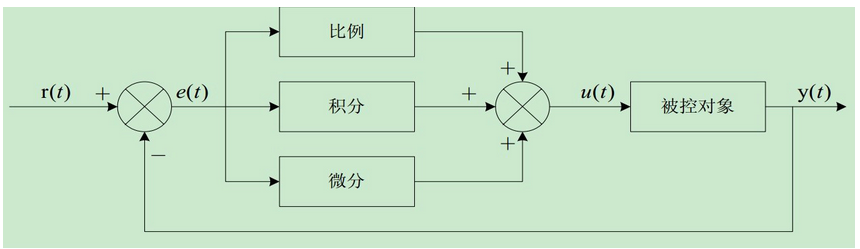
PID公式：

　　

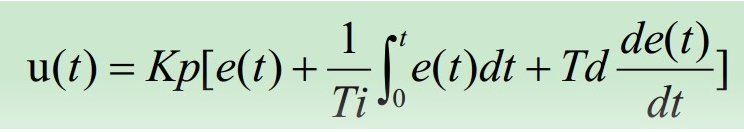
　　Kp：比例放大系数

　　Ti：积分时间常数

　　Td：微分时间常数

对丄式两边取拉普拉斯变换，得到PID控制器的传递函数;

　　G(S)=U(S)/E(S)=Kp+Ki/s+Kd*s,其中Td=Kd/kp,Ti=kp/ki。

线性系统稳态误差计算：

　　

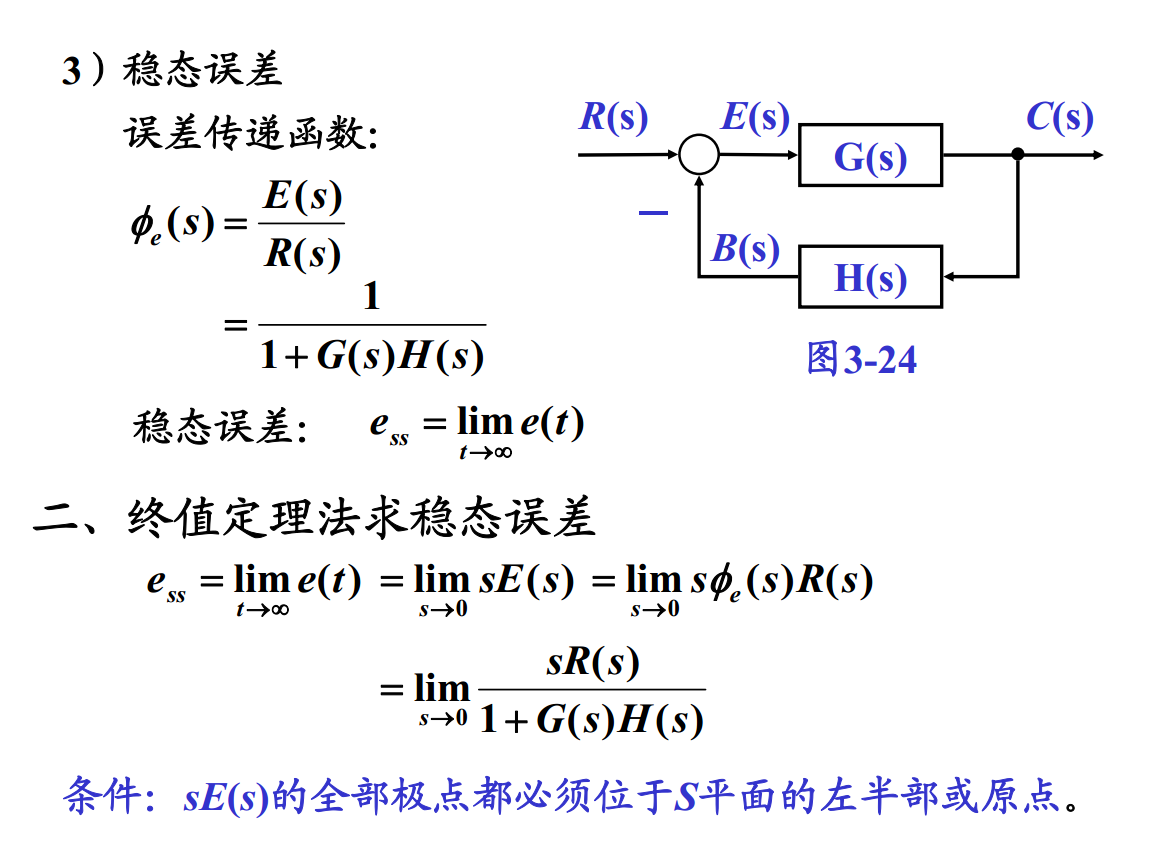
根轨迹：

　　

二，控制效果理解：

被控对象的传递函数：

　　

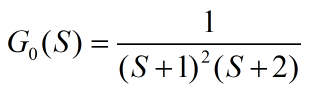
matlab仿真模型：

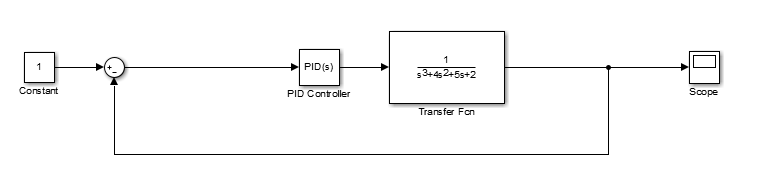
模型很简单，所以仿真波形就不贴出来了，感兴趣可以自己搭一个，然后看一看。

1,比例控制

　　当ki,kd给0时仿真结果：比例系数越大，可以使系统响应速度加快，也会减小静差，但是不能完全消除，同时也会使系统调节时间加长，震荡次数增加，过大还会导致系统不稳定。

　　当我们求出上面的模型中，只有比例控制时的系统传递函数时，通过上面的误差求解公式，我们可以得出，增大KP，会减小误差，但不会消除，而且通过画出根轨迹图也可以看出，当K大于18时，系统将变得不稳定。

　　下面是根轨迹图：

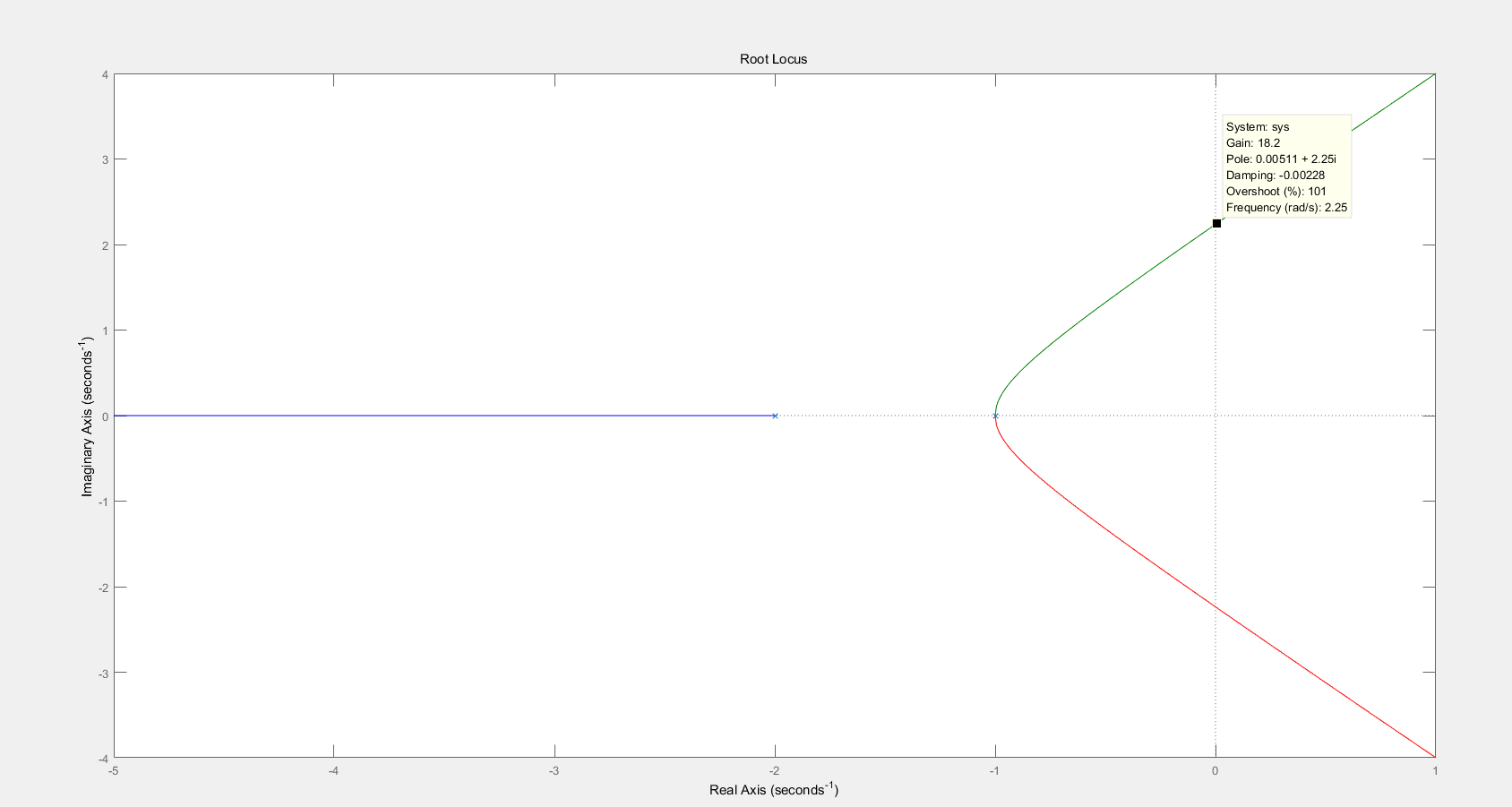
2，比例微分控制：

　　当只有Ki=0时，为比例微分控制。

　　仿真结果：微分作用可以提高系统相对稳定性，抑制系统的超调量，加快系统响应速度，但是过大，会使得系统对扰动的抑制能力减弱。

　　使用比例为分控制器，系统的开环传递函数相当于在负实轴上增加了零点。附加位置适当的开环零点，可使系统的稳定性和动态性能同时得到显著改善。
3，比例积分控制：

　　当Kd=0时，为比例积分控制。

　　仿真结果：加入积分，能有效消除系统的静差，加快达到参考值的时间，但是积分作用太强会使系统的超调量加大，甚至使系统出现震荡，对系统的瞬态特性也不利。

　　使用比例积分控制器。在给系统增加一个极点之外，也增加了一个位于负实轴的零点。

三，算法实现：

位置式：输出直接为控制量。

增量式：输出的是控制量的增量。

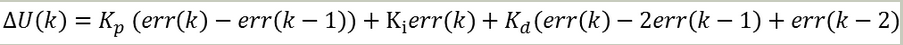
经典pid参数整定方法：

　　　　　　　参数整定找最佳， 从小到大顺序查。
                         先是比例后积分， 最后再把微分加。
                         曲线振荡很频繁， 比例度盘要放大。
                         曲线漂浮绕大弯， 比例度盘往小扳。
                         曲线偏离回复慢， 积分时间往下降。
                         曲线波动周期长， 积分时间再加长。
                         曲线振荡频率快， 先把微分降下来。
                         动差大来波动慢， 微分时间应加长。
                         理想曲线两个波， 前高后低四比一。
                         一看二调多分析， 调节质量不会低。