leetcode4：两个排序数组的中位数

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2 。

请找出这两个有序数组的中位数。要求算法的时间复杂度为 O(log (m+n)) 。

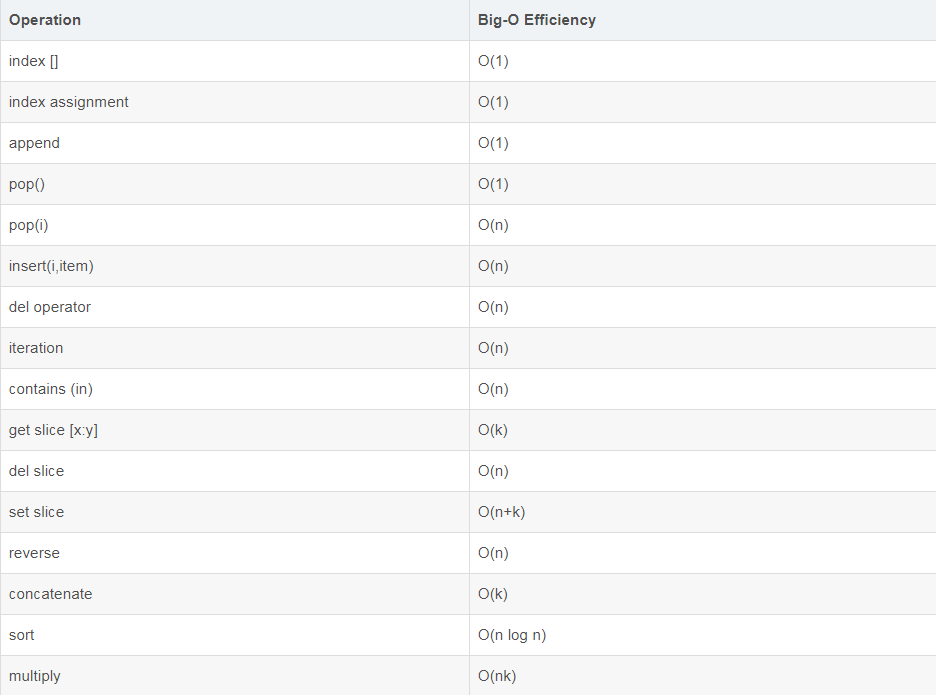
1.我的思路：直接用sort，时间复杂度应如图所示

 class Solution:
     def findMedianSortedArrays(self, nums1, nums2):
         """
         :type nums1: List[int]
         :type nums2: List[int]
         :rtype: float
         """
         nums = nums1+nums2
         nums.sort()
         n = len(nums)
         if n % 2 == 0:
             ans=(nums[int(n/2)]+nums[int((n/2)-1)])/2
         else:
             ans=nums[int(n/2)]
         return ans
 solution=Solution()
 solution.findMedianSortedArrays([1,3],[2])

2.网上的思路：

时间复杂度和空间复杂度都是O（m + n）,由于两个数组都是有序的，要找到中位数最好的方法就是将两个有序数组进行合并，创建一个大小为m+n的数组arr, 由后向前遍历，比较两个数组末尾元素的大小，将大的那个数存放到arr数组的尾部，然后大数数组的尾部下标向前移动，arr尾部下标也向前移动。直到某一个数组已经全部放进arr中，将剩下的那个数组全部拷贝进去，最后判断如果是奇数，则返回中间位的那个数，如果是偶数，返回中间两个数的平均数。