Fire Net（HDU-1045）（匈牙利最大匹配）（建图方式）

题意

有一个 n*n 的图，. 代表空白区域，X 代表墙，现在要在空白区域放置结点，要求同一行同一列只能放一个，除非有墙阻隔，问最多能放多少个点

思路

只有在墙的阻隔情况下，才会出现一行/列出现多个点的情况，那么可以考虑进行缩点，将同一行且没有墙体阻隔的区域缩成一个点，放到左点集中，将同一列且没有墙体阻隔的区域缩成一个点，放到右点集中，从而建成一个二分图

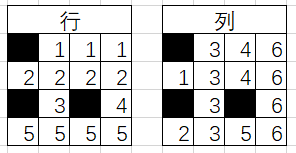
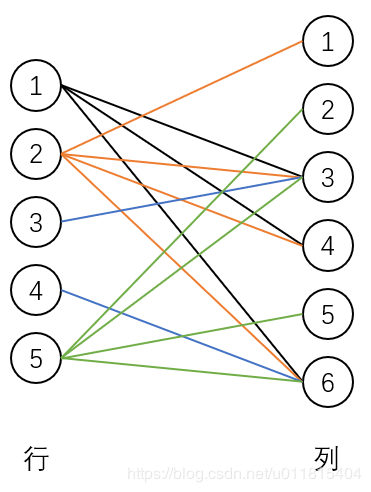
假设 i 为行编号，j 为列编号，若 i-j 之间存在一条边，就相当于在方格 (i,j) 上放了一个点，这个假设使得在没有墙体阻隔的情况下，i 行 j 列不能再放其他的点，那么在不考虑 不能同行同列 的情况下，将所有边连接起来，即行列缩点后，对应方格编号连边

建好图后，在图上求最大匹配即可

C++代码一

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define PI acos(-1.0)
#define E 1e-9
#define INF 0x3f3f3f3f
#define LL long long
const int MOD=1E9+;
const int N=+;
const int dx[]={-,,,};
const int dy[]={,,-,};
using namespace std;
int n;//n行n列
bool vis[N];//vis[i]表示是否在交替路中
int link[N];//存储连接点
int G[N][N];//存边
char str[N][N];
int x[N][N],cntX;//行点集
int y[N][N],cntY;//列点集
bool dfs(int x){
    for(int y=;y<cntY;y++){//对x的每个邻接点
        if(G[x][y]==&&!vis[y]){//不在交替路中
            vis[y]=true;//放入交替路
            if(link[y]==- || dfs(link[y])){//如果是未匹配点，说明交替路是增广路
                link[y]=x;//交换路径
                return true;//返回成功
            }
        }
    }
    return false;//不存在增广路，返回失败
}
int hungarian(){
    int ans=;//记录最大匹配数
    memset(link,-,sizeof(link));
    for(int i=;i<cntX;i++){//从左侧开始每个结点找一次增广路
        memset(vis,false,sizeof(vis));
        if(dfs(i))//找到一条增广路，形成一个新匹配
            ans++;
    }
    return ans;
}
int main(){

    while(scanf("%d",&n)!=EOF&&n){
        memset(x,,sizeof(x));
        memset(y,,sizeof(y));
        memset(G,false,sizeof(G));

        for(int i=;i<n;i++)
            scanf("%s",str[i]);

        //对行缩点
        cntX=;
        for(int i=;i<n;i++){//第i行
            for(int j=;j<n;j++){//第j列
                if(str[i][j]=='.')//同一区域
                    x[i][j]=cntX;
                if(str[i][j]=='X')//墙体阻隔
                    cntX++;
            }
            cntX++;//下一行
        }

        //对列缩点
        cntY=;
        for(int j=;j<n;j++){//第j列
            for(int i=;i<n;i++){//第i行
                if(str[i][j]=='.')//同一区域
                    y[i][j]=cntY;
                if(str[i][j]=='X')//墙体阻隔
                    cntY++;
            }
            cntY++;//下一列
        }

        //连边
        for(int i=;i<n;i++)
            for(int j=;j<n;j++)
                if(str[i][j]=='.')
                    G[x[i][j]][y[i][j]]=true;

        printf("%d\n",hungarian());
    }
    return ;
}

C++代码二

#include <bits/stdc++.h>
using namespace std;
int n;
struct node
{
    int a =  , b = ;
};
node id[][];
char mp[][];
bool link[][];
bool vis[];
int use[];
int hcnt,rcnt;

void dfsh(int x,int y){
    if(y <= n && mp[x][y] == '.'){
        id[x][y].a = hcnt;
        dfsh(x,y+);
    }
}

void dfsr(int x,int y){
    if(x <= n && mp[x][y] == '.'){
        id[x][y].b = rcnt;
        dfsr(x+,y);
    }
}

int find(int x)
{
    for (int s = ; s < rcnt; s++) {
        if (link[x][s] && !vis[s]) {
            vis[s] = ;
            if (use[s] ==  || find(use[s])) {
                use[s] = x;
                return ;
            }
        }
    }
    return ;
}

int main(int argc, char const *argv[])
{
    while(cin >> n && n){
        for(int i = ;i <= n ;i ++){
            cin >> mp[i] + ;
        }

            memset(id,,sizeof id);
            memset(link,,sizeof link);
            memset(use,,sizeof use);
            hcnt = rcnt = ;
            for(int i = ;i <= n;i ++){
                for(int j = ;j <= n ;j ++){
                    if(mp[i][j] == 'X'){
                        continue;
                    }
                    if(id[i][j].a == ){
                        dfsh(i,j);
                        hcnt ++;
                    }
                    if(id[i][j].b == ){
                        dfsr(i,j);
                        rcnt ++;
                    }
                    link[id[i][j].a][id[i][j].b] = ;
                }
            }
            int sum = ;
            for(int i = ;i < hcnt;i ++){
                memset(vis,,sizeof vis);
                if(find(i)) sum ++;
            }
            printf("%d\n",sum );
        }

    return ;
}

C++代码三

#define N 6
#include<queue>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
char k[N][N];
int book[N][N];
int n,ma;
void dfs(int step)
{
    if(step>ma)//保留每次能放得最大碉堡数
    {
        ma=step;
        return;
    }
    for(int i=; i<n; i++)
    {
        for(int j=; j<n; j++)
        {
            if(k[i][j]=='.'&&!book[i][j])//如果这个位置可以放碉堡
            {
                int a=i,b=i,c=j,d=j;
                //向四个方向覆盖，遇到边界或墙停止
                while(a>=&&k[a][j]=='.'){book[a][j]++;a--;}
                while(b<n&&k[b][j]=='.'){book[b][j]++;b++;}
                while(c>=&&k[i][c]=='.'){book[i][c]++;c--;}
                while(d<n&&k[i][d]=='.'){book[i][d]++;d++;}
                dfs(step+);//放置的碉堡数加1
                a=i,b=i,c=j,d=j;
                //取消覆盖
                while(a>=&&k[a][j]=='.'){book[a][j]--;a--;}
                while(b<n&&k[b][j]=='.'){book[b][j]--;b++;}
                while(c>=&&k[i][c]=='.'){book[i][c]--;c--;}
                while(d<n&&k[i][d]=='.'){book[i][d]--;d++;}
            }
        }
    }
    return;
}
int main()
{
    while(scanf("%d",&n)&&n)
    {
        for(int i=; i<n; i++)
            scanf("%s",k[i]);
        memset(book,,sizeof(book));
        ma=;
        dfs();
        printf("%d\n",ma);
    }
    return ;
}
 

DFS