BZOJ 5267 特工 (类FWT)

题意

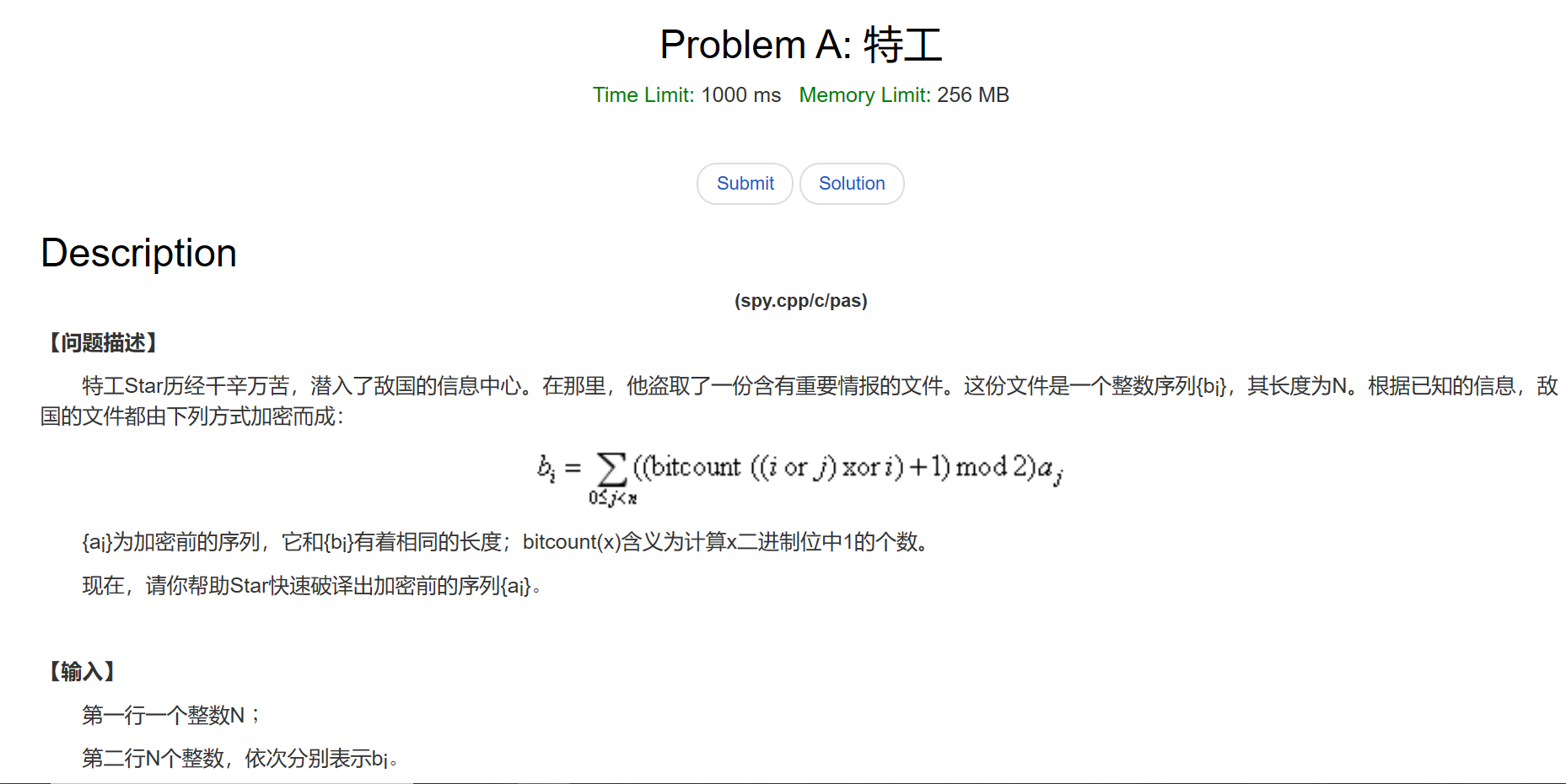
题解

从大到小枚举$l$, 把一个序列从$2^{l+1}$分成两个独立的$2^{l$，去除两半的影响。
设去除前的序列为$b$, 去除后序列为$b'$
则有$b_{2}{l+1}-1}-b_{2^l-1}=\sum{2^{l+1}-1}b_i$
考虑左边的一个位置$d$与右边的位置$d+2^{l$相对应
考虑一个序列$s_0$的第$i$位为$\text((i\ \text\ d)\ \text\ i)$，$s_1$为把$s_1$的$d$换成$d+2}l$的结果
显然两个序列左半部分完全一样，右半部分完全相反
设$z$为$b'$与$s_0$(或$s_1$)左半部分对应位置乘积之和，$y_0,y_1$分别为$b'$与$s_0,s_1$右半部分对应位置乘积之和
则$b'd=z,b'{d+2^l}=y_1$
且有方程$z+y_0=b_d,z+y_1=b{d+2^{l},y_0+y_1=b_{2}{l+1}-1}-b_{2^l-1}$
解之即可。

时间复杂度$O(n\log n)$.

代码

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<cassert>
#define llong long long
using namespace std;

char c[40000010];
int ns;
inline llong read(){
    while(c[ns]<'0'||c[ns]>'9')ns++;
    llong x=0;
    while(c[ns]>='0'&&c[ns]<='9')x=(x<<3)+(x<<1)+c[ns++]-'0';
    return x;
}

const int N = 1<<20;
llong a[N+3];
int n;

int main()
{
    c[fread(c,1,40000010,stdin)]=0; //input optimization
    n = read();
    for(int i=0; i<n; i++) a[i] = read();
    for(int i=(n>>1); i; i>>=1)
    {
        for(int j=0; j<n; j+=(i<<1))
        {
            llong tmp = a[j+(i<<1)-1]-a[j+i-1];
            for(int k=0; k<i; k++)
            {
                llong x = a[j+k],y = a[j+i+k];
                a[j+k] = (-tmp+x+y)>>1,a[j+i+k] = (tmp-x+y)>>1;
            }
        }
    }
    for(int i=0; i<n; i++) printf("%lld ",a[i]); puts("");
    return 0;
}